Рассмотрим структурную схему ЦЭП, изображенную на рис. 2б, и определим импульсную передаточную функцию замкнутого ЦЭП по сигналу ошибки. Входной сигнал импульсного элемента ε(t) зависит не только от внешнего воздействия nз(t), но и от выходной величины ЦЭП nд(t):
ε V(t) = nз(t)-nд(t) (9)
Так как импульсный элемент замыкается лишь в дискретные моменты времени t=n T, то последнее уравнение можно записать через решётчатые функции в виде:
ε V(nT) = nз(nT) - nд(nT) (10)
Подвергая уравнение (10) z-преобразованию и, учитывая теорему линейности, получим уравнение ошибки в изображениях:
Е(z)=nз(z)-nд(z) (11)
Из структурной схемы (рис. 2) также следует:
nд(z) = εν (z) Dkv(z) z{H(р)Wн(p)}. (12)
Подставив (10) в (11) найдем уравнение замкнутого ЦЭП относительно изображения ошибки:
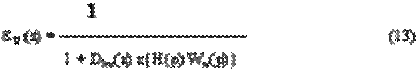
Если на вход ЦЭП подано ступенчатое воздействие
nз(t) =1(t),
z-изображение которой:
nз(z) = z/(z – 1) (14) то, подставляя (14) в (13) получим:
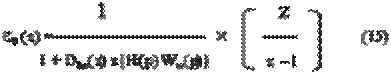
• Подставляя в (15) Dkv(z), H(р), Wн(p) и одновременно производя • z-преобразование для H(р) и Wн(p), получим:
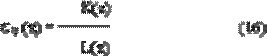
где
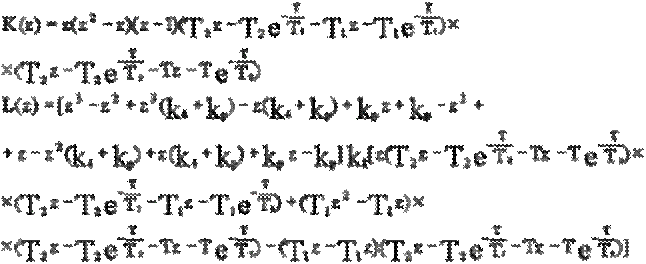 (17)
(17)
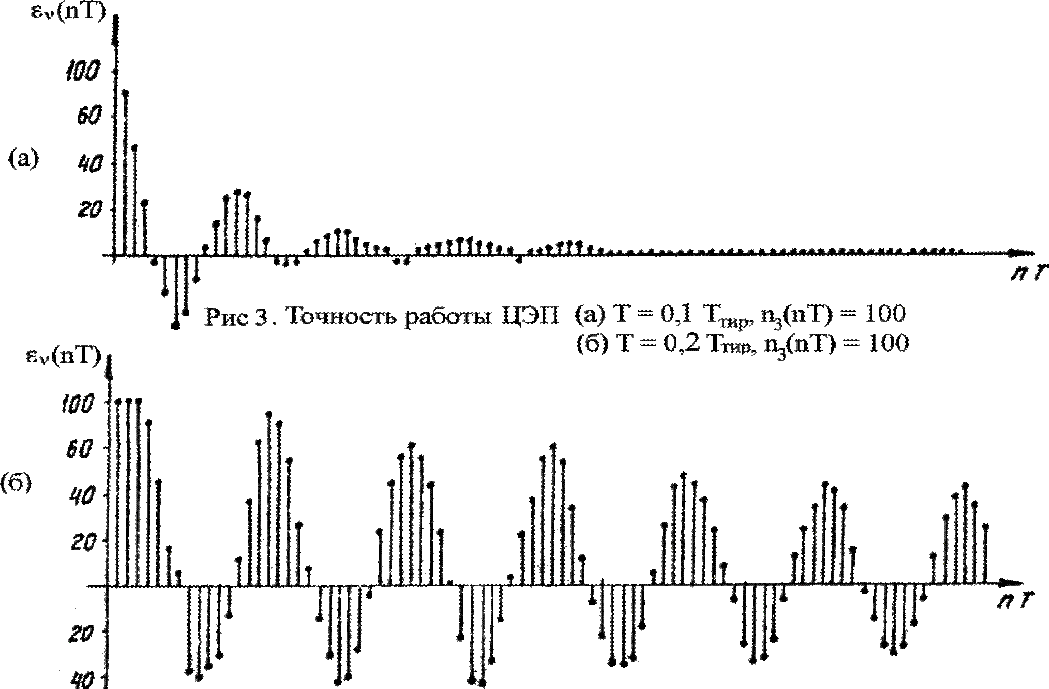
Решетчатую функцию εν[nT] (16) определим с помощью цифрового моделирования системы уравнений (3), описывающих работу ЦЭП. При цифровом моделировании ЦЭП были рассчитаны εν[nT] при различных значениях Т (рис. 3) и определено минимальное T = 0,1 Ттир(10-2c), при котором колебание частоты вращения не превысят заданных требований по ГОСТу.
Проведём анализ динамической точности ЦЭП по управляющему воздействию. Для оценки точности ЦЭП в установившемся режиме воспользуемся величиной установившейся ошибки при различных типовых воздействиях.
В замкнутом ЦЭП ошибка ε и управляющее воздействие nз связаны следующим уравнением относительно z-изображений:
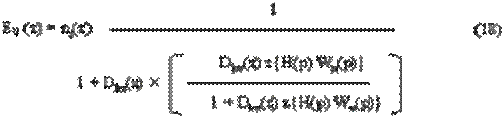
Установившаяся ошибка ЦЭП может быть вычислена по теореме оконечном значении дискретной функции:
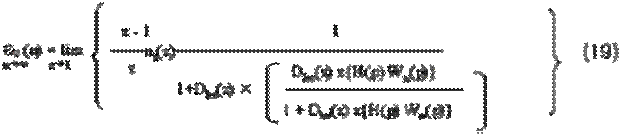
В качестве типового управляющего сигнала используем ступенчатое воздействие и воздействие с постоянной скоростью.
Если на вход ЦЭП подана ступенчатая функция
nз(t) = A01(t),
z-изображение которой:
nз(z) = A0z/(z – 1) (20) то в соответствии с (19) установившаяся ошибка записывается как:
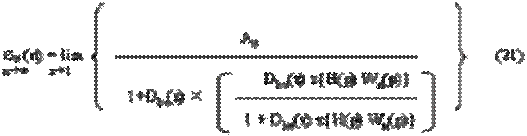
При входном воздействии hз(t) = A1(t), линейно зависящем от времени, zизображение управляющего сигнала:
nз(z) = A1T0z/(z – 1)² (22) а установившаяся ошибка, согласно (19) определяется с помощью соотношения:
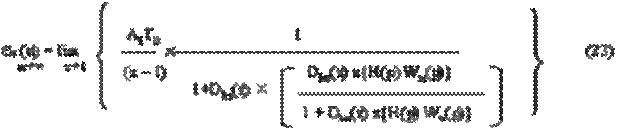
Ряд ошибок при использовании типовых управляющих сигналов ступенчатого воздействия с постоянной скоростью запишутся в следующем виде:
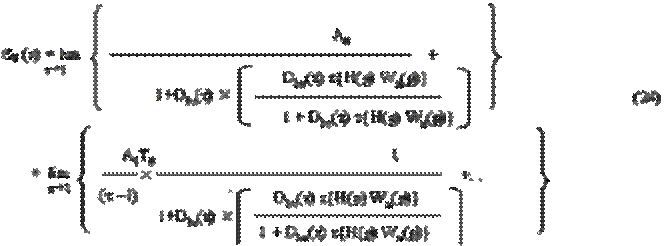
Расчет установившейся ошибки ЦЭП выполнен на ЭВМ при цифровом моделировании. При расчете ЦЭП в установившемся режиме работы представляет интерес случай, когда на входы ЦЭП поданы сложные, почти периодические, управляющие или возмущающие воздействия вида:
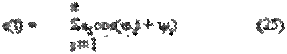
где ai - амплитуда, ωi - частота, ψ i - начальная фаза, i - индекс составляющей, е - число составляющих.
В самом общем случае такой расчет содержит ряд однотипных операций, выполняющих последовательно: определение сигналов на выходе линейной системы и на выходе элемента перемножения; сортировку совокупности сигналов по спискам с расположением элементов в порядке возрастания значений частоты, отрабатывание малых составляющих, математическую обработку некоторого расчетного приближения для вывода данных. На рис 4(а,б) представлены переходные процессы установившейся ошибки εV[nT] ЦЭП, при периодическои управляющем воздействии n3[nT].
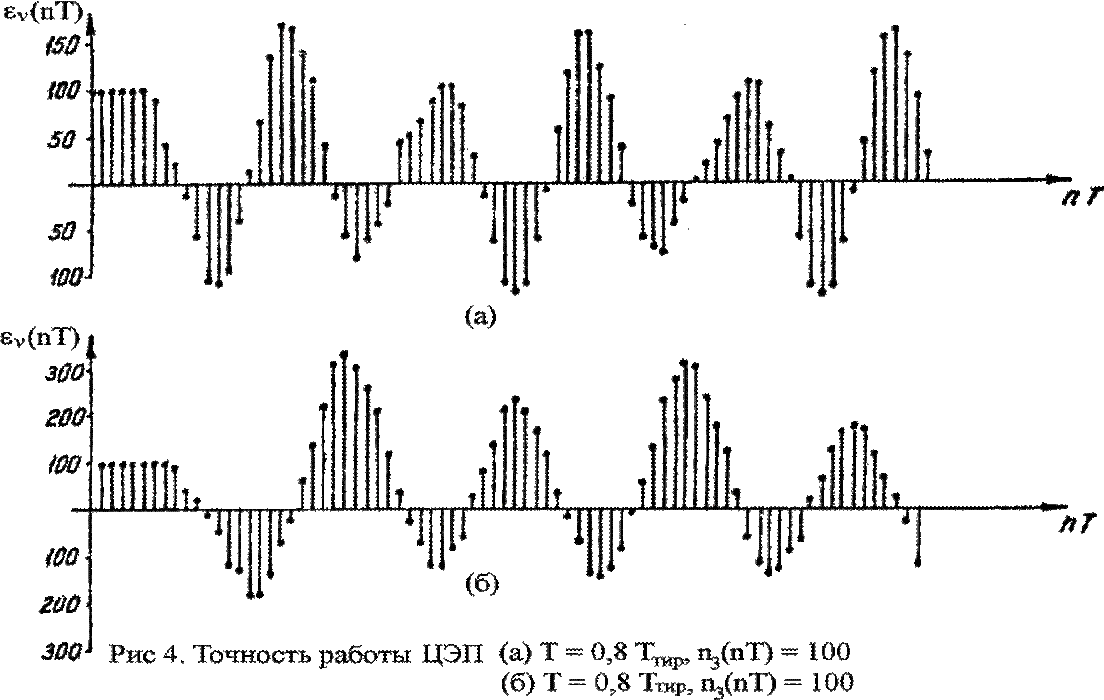
Литература.
1. Буянкин В.М., Кравец В.А., Семенов В.С. Изучение цифрового электропривода постоянного тока с прямым микропроцессорным управлением: Методические указания к лабораторной работе по курсу “ Основы электропривода”/ Под ред. Ю.И. Даниленко.-М.: Изд-во МГТУ, 1982.-12с.
2. Буянкин В.М., Шамгулов Р.О. Программно-математическое обеспечение микропроцессорного привода в лаборатории электропривода. М.,19991.6с. Деп. В ВНИИВО 06.07.91, N1151-91
3. Герман-Галкин С.Г. и др. Цифровые электроприводы с транзисторными преобразователями. Л.: Энергоиздат,1986.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.