Фундаментальные исследования с использованием математической модели и цифрового моделирования микропроцессорного привода, страница 2

Для отображения информации об угле поворота ϕ и частоте вращения ϕ вала электродвигателя на стенде предусмотрена цифровая индикация. Угол поворота отображается при помощи выполненного на светодиодах семисегментного индикатора. На индикаторах при этом появляются десятичные числа, соответствующие углу поворота вала электродвигателя.

При помощи программатора осуществляется кодовое задание входных параметров в микро-ЭВМ.

На рис. 2а изображена функциональная схема ЦЭП, работающего в регулируемом режиме. Цифровой сигнал ошибки ε_V[nT] вычисляетя в микро-ЭВМ, в выхода которой, реализуется закон регулирования. Цифровой решётчатый сигнал Θ_o[nT] поступает на вход идеального импульсного элемента Иэ3 и превращается в сигнал: Θ*_o[nT] = Θ(t)δ(t-nT) = Θ(τ)σ _т(t), (1) где n = 0,1,2,...; σ _т(t) - δ функция.

Далее сигнал Θ*_o[nT] поступает на формирующий элемент, представляющий собой экстрополятор нулевого порядка с передаточной функцией:

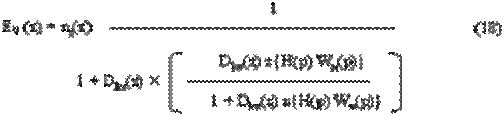
где k_им =1 - коэффициент усиления импульсного элемента.

Сигнал с выхода формирующего элемента поступает в непрерывную часть ЦЭП.

При анализе влияния периода дискретности по времени Т на устойчивость опишем работу ЦЭП дифференциальными уравнениями (З) и рассмотрим работу ЦЭП в регулируемом режиме

•  где n_з - заданная частота вращения; 

•  n_д - частота вращения электродвигателя;  

•  ε₁- ошибка регулирования в путевом контуре; 

•  D_ks - передаточная функция путевого контура;  

•  ε_s - величина на выходе путевого регулятора; 

•  k_us - коэффициент усиления путевого регулятора;  

•  ε_V - ошибка регулирования в скоростном контуре; 

•  D_kv - передаточная функция скоростного регулятора; 

•  k_n- коэффициент пропорциональной составляющей ошибки 

•  скоростного регулятора;

•  k_u - коэффициент интегральной составляющей ошибки скоростного 

•  регулятора;

•  Θ ₀, ε_s - величины на выходах скоростного и путевого регуляторов; 

•  Н(р) - передаточная функция формирующего элемента;  

•  Θ - величина на выходе формирующего элемента; 

•  U_т - напряжение на выходе тиристорного преобразователя; 

•  i_я - ток якоря в цепи электродвигателя; 

•  Е_пр - э.д.с. исполнительного электродвигателя; 

•  М_тр - момент трения; 

•  М_дв - движущий момент, развиваемый электродвигателем, 

•  В качестве примера возьмем данные электродвигателя постоянного тока ПБСТ-22 /Р_н = 0,6 кВт, U_тн = ll0 В, i_ян =7 А/. 

•  L_э = 3,1×10^-2 Гн - эквивалентная суммарная индуктивность якорной 

•  цепи;

•  R_э = 3,5 Ом - эквивалентное сопротивление якорной цепи; 

•  k_Е = 81×0^-1 В×с/рад - коэффициент э.д.с.; 

•  k_м = 9×10^-1 Н×м/А - коэффициент момента; 

•  k_тир = 1,1 В×с/рад - коэффициент передачи тиристорного 

•  преобразователя;

•  Т_тир = 10^-2 с - постоянная времени тиристорного 

•  преобразователя;

•  I = 8×10^-2 кГм² - суммарный момент инерции, 

•  приведенный к валу электродвигателя;

•  k_тр = 1,4×10^-3 кГ×м²/с - коэффициентвязкого трения на валу 

•  электродвигателя;

•  По системе уравнений (3) составлена математическая модель ЦЭП (рис. 2б). 

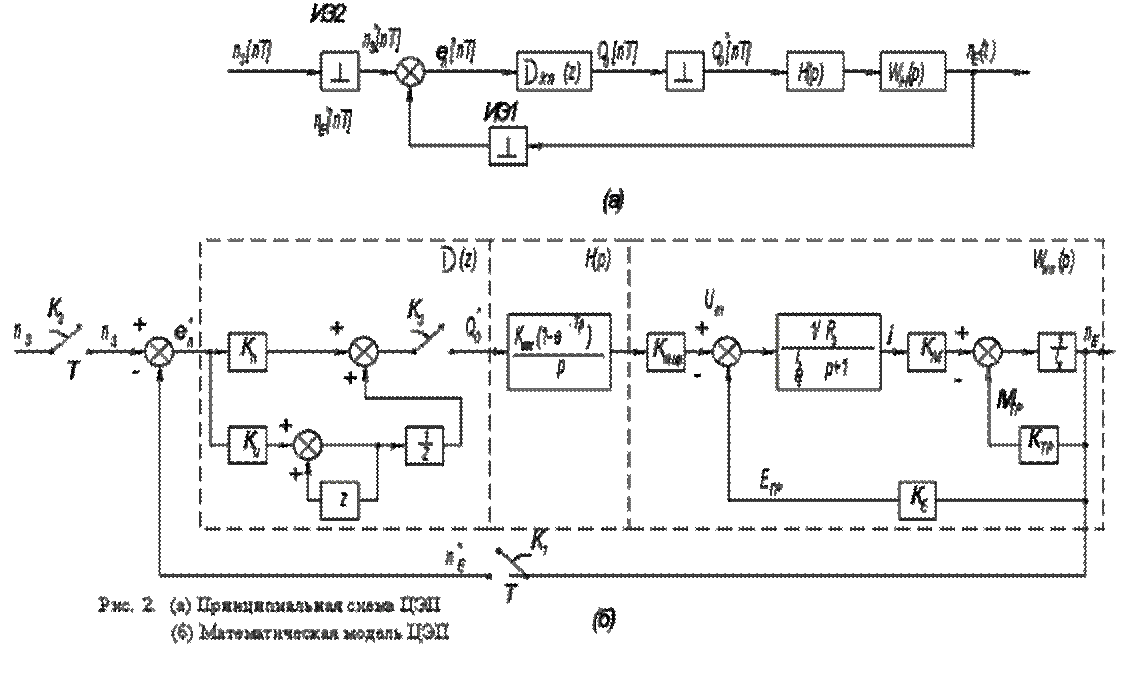
Ключи KI, К2, КЗ иллюстрируют дискретность по времени приёма информации с датчика обратной связи, задания и выдачи цифрового кода в импульсно-фазовую систему управления тиристорного преобразователя, который для упрощения расчетов представлен безынерционнымзвеном. Математическая модель представляет собой линейную цифровую систему с амплитудно-импульсной модуляцией.

Последовательное соединение формирующего элемента и непрерывной части тиристорного преобразователя, электродвигателя постоянного тока образует, так называемую, приведенную непрерывную часть ЦЭП, передаточная функция которой имеет вид:

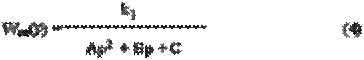
где k₁ = k_м k_тир = 8,8×10^-1 кГ м² Ом /(с/рад);

А = L_э I = 2,5 IO^-3 Ом с кГ м²;

В = I R_э + k_тр L_э = 2,8 1O^-1 кГ м² Ом;

С = k_тр R_э + k_Е k_м = 6,4 10^-1 Ом кГ м²/(рад/с).

                                

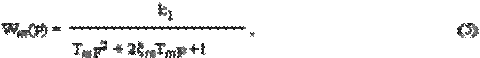
Т₀₁ = √ А/С ; ξ ₀₁ = (В/2С)× √ С/А

С помощью z-преобразования Лапласа находим передаточную функцию ЦЭП в разомкнутом режиме:

W_h(z) = D(z) z{H(р) W_нт(p)}. (6)

Для нахождения передаточной функции W_h(z) в ω-преобразованном виде произведем подстановку:

                          

Тогда передаточная функция z{H(р) W_нт(p)} в ω-преобразованном виде будет иметь вид:

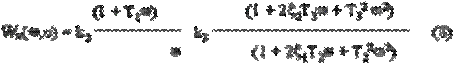
Решётчатую функцию n_д[nT] при ступенчатом воздействии n_з[nT]определим с помощью цифрового моделирования системы уравнений 3, описывающих работу ЦЭП.

Проведём анализ влияния дискретности по времени на точность работы ЦЭП. В ЦЭП из-за наличия квантования по времени и режимов прерывистого тока возможны пульсации тока якоря, которые вызывают дополнительный нагрев и вибрации электродвигателя, ухудшают коммутацию, в тиристорном преобразователе. Пульсации тока могут вызвать колебания частоты вращения и повлиять на механические характеристики электродвигателя.