Потенциальная точность измерений, страница 2

способы обработки результатов измерений и оценки по­казателей точности измерений;

требования к квалификации операторов;

требования к. технике безопасности.

В аттестатах на методики выполнения измерений указы­вают:

назначение и область применения методики;

типы и номера экземпляров средств измерений, используемых для проведения измерений. Номер экземпляра сред­ства измерений в аттестате не указывается, если значения показателей точности измерений, указанные в аттестате, оп­ределены с учетом возможности применения любого экземп­ляра средства измерений данного типа;

технические характеристики вспомогательных устройств, необходимых для выполнения измерений;

метод измерений;

порядок подготовки и выполнения измерений;

численные значения показателей точности измерений;

межповерочные интервалы для средств измерений и но­менклатуру нормативных документов, согласно которым должна проводиться их поверка;

требования к квалификации операторов;

требования техники безопасности.

Точность измерений во многом зависит также от алго­ритма обработки экспериментальных данных. Этим обуслов­лено требование аттестации алгоритмов.

В отдельных областях и видах измерении при совре­менной эталонной базе достигнута точность, обеспечивающая возможность выполнения измерений на   молекулярном уровне. Формальным отражением этого служит появление пос­тоянной Больцмана k = 1,38 • 10 ^-23 Дж/К в выражениях, опи­сывающих влияющие факторы, с которыми нужно считаться. Частицы вещества — атомы, молекулы, а также электричес­кие заряды совершают непрерывные хаотические движения, интегральная интенсивность которых характеризуется тер­модинамической температурой Т. Чем интенсивнее движе­ния, называемые флюктуациями, тем выше абсолютная температура Т. Флюктуации создают   шумовой эффект, ог­раничивающий точность  измерения физических величин. Мощность шума Р_Ш определяется уравнением Найквиста:

,

где  f — ширина полосы пропускания прибора. Иногда это выражение дополняется спектральным коэффициентом N, учитывающим дробовый эффект в электронных приборах и другие явления.Тогда

.

Вместо мощности Р_Ш можно рассмотреть энергию шума G_Ш , причем                                           

G_Ш = 4 k N Т.

Если исходить из того, что энергия полезного сигнала Р × t, где Р — мощность, a t — время измерения, должна быть боль­ше энергии шума, то возможность выполнения измерений на молекулярном уровне будет ограничиваться требованием выполнения неравенства

 Р × t  G_Ш .

Используя различия в статистической природе шумов и полезных сигналов, во многих случаях удается преодолеть ограничения, обусловленные законами термодинамики. В частности, не когерентность шума позволяет при многократ­ном измерении, накоплении, оптимальной фильтрации и пу­тем использования других приемов обеспечить выполнение                              

 измерений при отношении .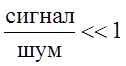

Принциальные ограничения следующего уровня обуслов­лены дискретностью измеряемых величин (нельзя, например, измерить заряд, меньший заряда электрона) или флюктуация­ми, определяемыми дискретностью вещества и энергии. Точ­ность измерений на этом уровне ограничивается законами квантовой механики.

Формальным отражением выхода на квантовомеханический уровень точности измерений  служит появление в ма­тематическом описании факторов, которыми нельзя пренеб­регать, постоянной Планка h = 6,63 • 10 ^{- 34} Дж/Гц. Одним из таких факторов является принцип неопределенности Гейзенберга, связывающий (через постоянную Планка) точность измерения координаты и импульса частицы, времени и энер­гии, а также других пар физических величин. Точность измерений в таких условиях становится предметом разум­ного компромисса.

8.2. ОПРЕДЕЛЕНИЕ ТОЧНОСТИ ИЗМЕРЕНИЙ РАСЧЕТНЬМ ПУТЕМ

Потенциальная точность измерений,   определяемая на любом уровне развития науки и техники точностью госу­дарственных эталонов, в обиходе   недостижима. Поэтому естественно встает вопрос о реально достижимой точности измерений. При решении этого вопроса всегда исходят из анализа конкретной измерительной задачи и стараются, как можно полнее учесть всевозможные ограничения.

Пусть, предположим, apriori известно, что сигнал X(t) на выходе линейного измерительного преобразователя с ко­эффициентом преобразования, равным 1, будет представлять собою смесь полезного сигнала X(t) = Q = const и шумовой помехи N(t) в виде нормального стационарного случайного процесса со средним значением, равным нулю, обусловлен­ной внешними и внутренними влияющими факторами. Воз­можны следующие способы измерения неизвестного значе­ния Q:

усреднение Х (t) по времени (в течение одной реализа­ции);

усреднение Х (t)  по множеству значений, относящихся в каждой реализации к одному и тому же моменту вре­мени;

усреднение Х (t) и по множеству, и по времени. Наряду с этим метрологическое обеспечение измерений мо­жет быть организовано по-разному. В одном из вариантов (см. рис. 161, а) информация о размере единицы передает­ся только измерительному преобразователю. В этом слу­чае в сигнал  на выходе измерительного преобразователя

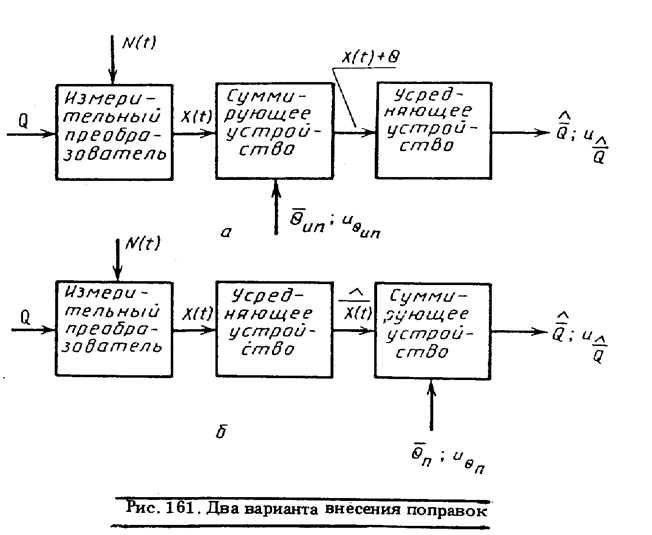
может вноситься поправка. Точное значение ее обычно не­известно, что учитывается ситуационной моделью поправ­ки. Усредняющее устройство затем выполняет необходимые математические операции.

Во втором варианте информация о размере единицы пе­редается измерительному прибору в целом, включающему в себя и измерительный преобразователь и усредняющее устройство. Поправка в таком случае вносится при необ­ходимости в показание прибора— рис. 161, б.

Показателем точности служит аналог стандартного откло­нения результата измерения . Выражения для него при­ведены в табл. 50, где  — дисперсия шумовой помехи;

 — аналог среднего квадратического отклонения в ситуа­ционной модели поправки;  — интервал корреляции нор­мального стационарного случайного процесса Х (t) ; Т_P — дли­тельность реализации того же процесса; п — число реализа­ции. При составлении табл. 50 учтено, что в первом ва­рианте поправка вносится в мгновенные значения X(t) с последующим цифровым усреднением полученного массива. Поправка на неточность дискретного усреднения имеет дисперсию .

Табл. 50 позволяет проанализировать зависимость точ­ности измерений от множества факторов. Так, например, очевидна зависимость точности от объема экспериментальных данных (п, Тр). Ограничение объема экспериментальных дан­ных ограничивает точность измерений. Видна зависимость точности от конструктивных и схемотехнических решений (способа усреднения, значения  ). Есть возможность аль­тернативного выбора, а в случае ограничений на выбор — непосредственного  расчета точности измерений. Двумя вариантами  представлены подходы к метрологическому обеспечению, качество которого определяется значениями и . Весьма наглядна зависимость точности от априорной

ной информации о влияющих факторах (, ). Если точ­ной информации о параметрах                               помехи нет, а известен лишь закон распределения их вероятности, то

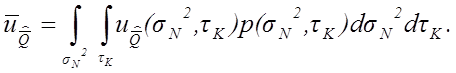
При р(,) = р()р() этот двойной интеграл в каж­дом конкретном случае вычисляется просто.

По табл. 50 в каждом конкретном случае легко найти минимальное значение , т.е. определить максимально воз­можную точность при выбранных условиях и ограничениях.

Подобным образом рассчитывается и анализируется точ­ность измерений и в более сложных случаях, отличающих­ся тем, что приходится учитывать большее количество фак­торов.