Регулирование частоты вращения в системе “ТП-ДПТ НВ”. Схема, принцип действия и основы проектирования асинхронных ЭП с автоматизированным реостатным регулированием частоты вращения

Билет24

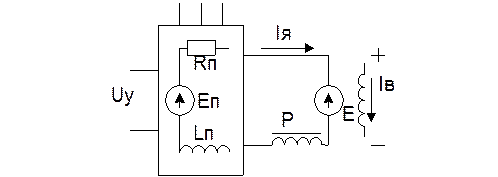1.Регулирование частоты вращения в системе “ТП-ДПТ НВ”.

Р- сглажив-й дроссель

Внешняя х-ка ТП приближ-ся к линейной только в реж. прерыв-го тока. Регулиров-ая х-ка линеариз-ся, как и в случае тиристорного возбудителя. Коэф-нт   передачи преобр-ля для анализа динамики определ-ся в окрестностях угла рег-ия a=(p/2). Для расчета стат-их хар-к обычно усредняется Кп=(Edo/(Uoпmax/2)).

Как стат-ие так и динам-ие процессы в якорной цепи опред-ся средними знач-ми напр-ия и тока за период коммутации тиристоров.   В итоге, преобраз-ль представ-ся в виде источника напряжения с внутренними параметрами: Eп, Rп, Lп.

Rп= Rтр(Rк.р.)+Rк;    Lп=Lтр(Lк.р.)

Rя=Rяд+Rп+Rр

Lя=Lяд(Lп)+Lр

К_п’Uу=(Т_пр+1)w₀;

М(Т_яр+1)=bс(w₀-w);

bc=((кФ)²/Rя).

Стру-ра системы полностью аналог-на обобщенной сис-ме.

Для приведенного преобр-ля, реверсивного с раздельным управлением, в зоне малых нагрузок им. место  режим прерыв-го тока. При этом внешняя характер-ка смягчается, что уменьшает жесткость мех-ой хар-ки

Рис.2 Нелин-ть в нуле из-за уравнительных токов.

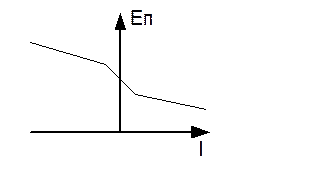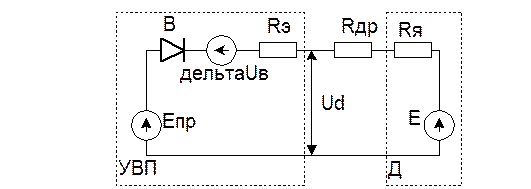
Для режима непрерывного тока можно составить эквивалентную схему для сис-мы “управляемый вентильный преобразователь - ДПТ” (УВП-ДПТ). Для данной эквивалентной  схемы можно записать уравнение электрического равновесия

Епр-DUв-Е=I_dR ,   (1)

где R=Rэ+Rдр+Rя

Е=kФw   (2)

Е- противо-ЭДС ДПТ НВ

DUв-падение напряжения на силовом вентиле

На основании (1) и (2) находим электромеханическую характеристику ДПТ НВ:

w=((U_d0cosa-DUв- I_dR)/ kФ)

Учитывая,  что в системе УВП-Д электромагнитный момент двигателя М= kФI_d получаем уравнение механ-ой характер-ки

w=((U_d0cosa-DUв/ kФ)-MR/(kФ)²)

Жесткость механ-х хар-ик ДПТ НВ в разомкнут сис-ме УВП-Д меньше чем в разомкнут сис-ме Г-Д по причине большего суммарного сопротивления якорной цепи.

Регулир-е скорости ЭД в сис-ме УВП-Д осущес-ся изменением угла открывания вентилей  a, что приводит к изменению среднего значения выпрямленной ЭДС Епр. В выпрямительном режиме УВП угол a изменяется от 0 до p/2, а в инверторном от p/2 до p-(g+d), где g-угол коммутации, d-угол восстановления запирающий свойств вентилей. В режиме инвертирования выпрямленная ЭДС Еd отрицательная.

Скорость идеального холостого хода ДПТ НВ в двигательном режиме

w’₀=(U_d0cosa-DUв/ kФ)

в тормозном режиме

w”₀=-( U_d0cosa_и-DUв/ kФ)

где a_и=p-a,    a_и- угол инвентирования однако, скорость идеального холостого хода является фиктивной величиной, т.к. при Id<Iкр (Iкр-критический непрерывный ток) наступает режим прерывистого тока, для которого приведенные выражения не будут справедливыми. Режим прер-го тока обусловлен тем, что со снижением нагрузки уменьш-ся кол-во энергии, запасенной в индуктивностях якоря и дросселе Др, и наступает момент, когда создаваемая в индуктивностях ЭДС самоиндукции оказывается недостаточной для поддержания тока при отрицательных напряжениях на анодах вентилей. Это приводит к увеличению среднего выпрямленного  напряжения за время работы вентиля, а значит, и скорости идеального холостого хода. При углах открывания менее p/m (m-пульсность) скорость ЭД стремится к некоторому максимуму, который определяется амплитудой напряжения, а при больших  a - до граничного значения, которое определяется мгновенным значением вторичной обмотки трансф-ра в момент подачи управляющего импульса. Нарушение непрерывности выпрямленного тока приводит к неудовлетв-ой форме мех-х хар-ик, вызывает дополнительные гармоники тока, которые увеличивают нагрев ЭД.

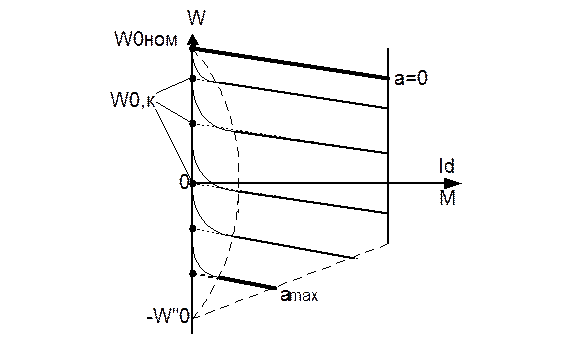Особенности: малые потери энергии, высокое быстрод-ие, низкое кач-во энергопотреб-ия (генерация высших гармоник в сеть), низкий cosj ;   j⁽¹⁾=a+(g/2).

Для повышения точности систему замыкают отрицательной обр-ой связью по скорости.

Кп(Uзc-Косw)=(Т_пр+1)e_п;

e_п=cw+Rя(Т_яр+1)i_я.

i_я=(M/c);   Koc=(DUoc/Dw)

KпUзс-КпКосw=с(Т_пр+1)w+Rя(Т_пр+1)(Т_яр+1)i_я

с((Т_пр+1)+( КпКос/с))w=КпUзc-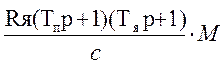

w=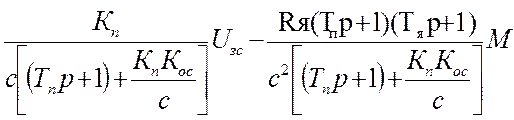

Статическая характеристика:

w=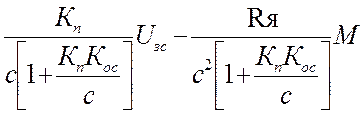

для замкнутой системы модуль жесткости

bзам=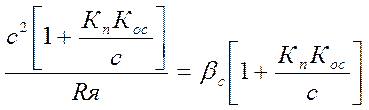

Cвязь между статическими характеристиками при w_{0 зам}=w_{0 разом}  

Sх зам=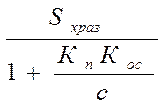

Для получения абсолютно жесткой хар-ки с bзам=¥, или Sх зам=0 ÞКос=¥

Для исходной системы уравнений учтем уравнение движения, при условии, что Тп=0

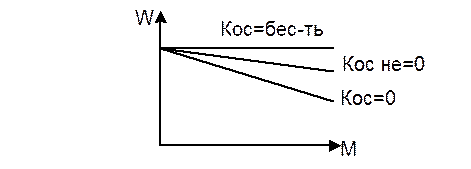i_я=(Mc/c)+(J/c)pw

KпUзс-КпКосw= сw+(Rя/c)(Т_яр+1)Мс+(JRя/с)(Т_яр+1)рw

с((RяJ/c²)(Т_яр+1)p+((КпКос/с)+1)w= KпUзс-(Rя/c)(Т_яр+1)Мс

Характеристическое уравнение для скорости

Тм(Т_яр+1)+(КпКос/с)+1)=0

Таким образом, введение ОС по скорости подобно уменьшению электромеханической постоянной времени. В результате корни уравнения будут иметь меньшую вещественную часть α (р=-α±jΩ) и более высокое значение Ω, т.е. колебательность системы возрастает при более длительном затухании колебаний и рассматривая данную систему регулирования как САР с П-регулятором скорости (входящим в УП) получаем, что при широком диапазоне регулирования скорости (100 и более) получить требуемую статическую точность при заданном качестве переходных процессов не всегда возможно. Когда допускает требуемое быстродействие можно использовать