Физика \ Теория электропривода

Математическая модель и структурная схема АД с частотно-токовым управлением. Номинальная и текущая частоты вращения поля, страница 2

J*dw / dt + Mc(t) = 3/2*Kr*isy*Yrx , где Tr = Lr / Rr – постоянная времени ротора .

Из системы уравнений ( 6.2.4.) видно, что приняв в качестве управляющих воздействий составляющую тока статора isx и синхронную скорость w1 , можно воздействовать на потокосцепление Yrx и частоту вращения w ротора АД. Это и составляет, как известно, сущность частотнотокового управления АД.

В преобразовании по Лапласу математическая модель АД ( 4.3.4.) можно представить следующим образом

 


Yrx(p) = (Xm/w1n) / ( Tr*p + 1 )*Isx(p) ,

Isy(p)  = 1/ ( Kr*Rr )*L[ Dw*Yrx ] ,                                        (6.2.1.)

w(p)    = { 3/2*Kr*L[ Yrx*isy ] – Mc(t) }*1/ ( J*p ) , где  Dw = w1 – w – скольжение ;

L – символ прямого преобразования по Лапласу ;

Yrx(p) , Isx(p) , Isy(p) , w(p) , Mc(p) – операторные  изображения временных переменных Yrx , isx , isy ,

w , Mc(t) .

Системе уравнений ( 4.3.5.) соответствует структурная схема АД с частотно-токовым управлением , представленная на рис. 4.4., где блоками перемножения временных переменных условно изображены интегралы свёртки

L [ … ] .


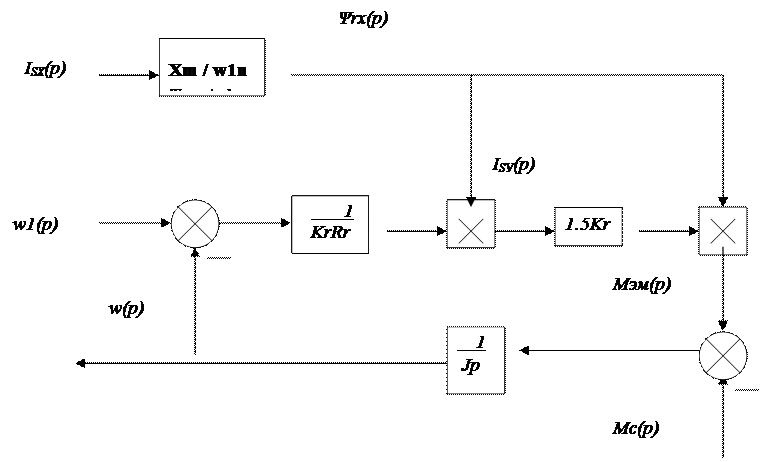
Рис. 6.1. Структурная схема АД при частотно-

токовом управлении .


6.3.  Синтез регуляторов.

6.3.1. Синтез регулятора тока.

Для того чтобы произвести данную операцию составляется структурная схема контура тока и по ней запишем передаточную функцию по управлению (далее ПФ) разомкнутого контура.

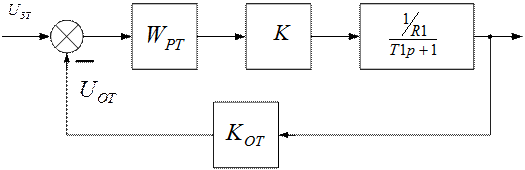
Рис.6.2. Структурная схема контура тока.

По рис.6.2.  составляем ПФ контура тока :

Принимаем частоту среза wср=100 c-1;

Tрт = 1/wср=1/100=0.01 c;

Коэффициент регулятора тока имеет вид :

Крт = 1/(1/R1)·1/K·1/Koт =1/73.637·1/76·1/0.0175=0.0102;

Регулятор тока имеет вид:

Wрт = Kрт·1/Tрт·(T1p+1);

Wрт = 0.0102·1/0.01p·(0.018925p+1)

6.3.2. Синтез регулятора скорости.

 

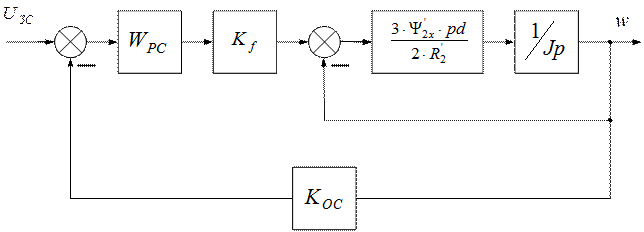
Рис.6.3. Структурная схема контура скорости.

Вначале рассмотрим внутренний контур

W’(p) = 3/2·(ψ2x2/R2’) ·pd·(1/Jp)  /  (3/2·(ψ2x2/R2’) ·pd·(1/Jp)+1) = 3/2·(3.1432/0.0125) ·2·(1/125.7p)  /  ( 3/2·(3.1432/0.0125) ·2·(1/125.7p)+1) = 1/(0.053p+1);

Малую постоянную времени  Tм примем равной Tрт, тогда

w’ср=1/2Tм = 1/2·0.01 = 50 c-1;

Tрс = (1/ w’ср) ·Koc·Kf = 1/50·0.016·62.8 = 0.02 c;

Рассмотрев внутренний контур преобразуем структурную схему контура  скорости.

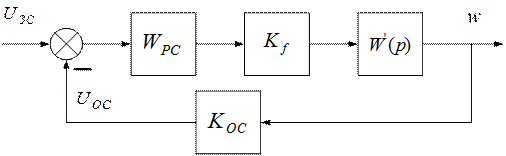
Рис.6.4. Структурная схема контура скорости после упрощения.

Исходя из рис.6.4  получаем

Wc(p) = Wрс·Kf ·Koc·W’(p) = Wрс·62.8·0.016·(1/0.053p+1);

В результате регулятор скорости имеет вид:

Wрс = (0.053p+1) ·1/0.02p.

6.4. Определение статической ошибки.

Рассмотрим контур скорости.

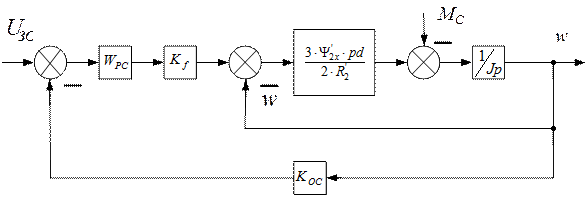
рис.6.5. Контур скорости.

Для того чтобы получить передаточную функцию замкнутой САУ необходимо преобразовать контур скорости к должному виду.

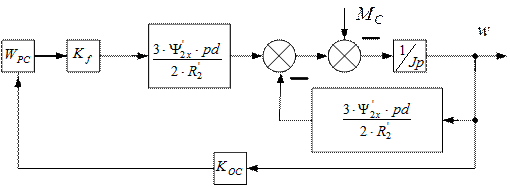
рис.6.6. Контур для определения ошибки.

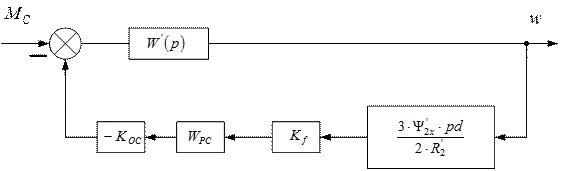
рис.6.7. Структура для возмущения.

;

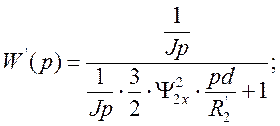
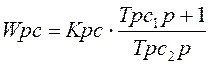Передаточная функция замкнутой САУ по возмущению имеет вид:

;

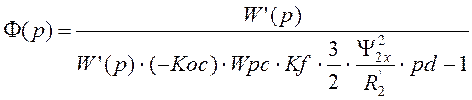Подставляя все соответствующие выражения для полученных нами ранее регуляторов получаем следующее:

 

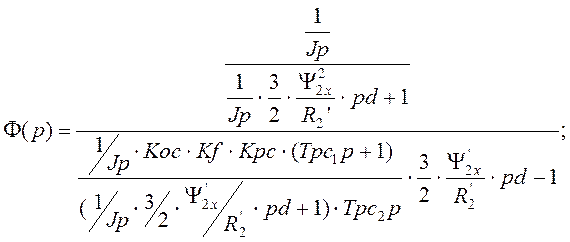
Проведя соответствующие математические преобразования и вычисления приведем выражение к более упрощенной форме.

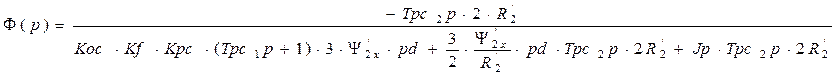
Подставляя вместо оператора p значение 0, получаем:

;

Следовательно статическая ошибка отсутствует.

6.5. Анализ динамики электропривода.

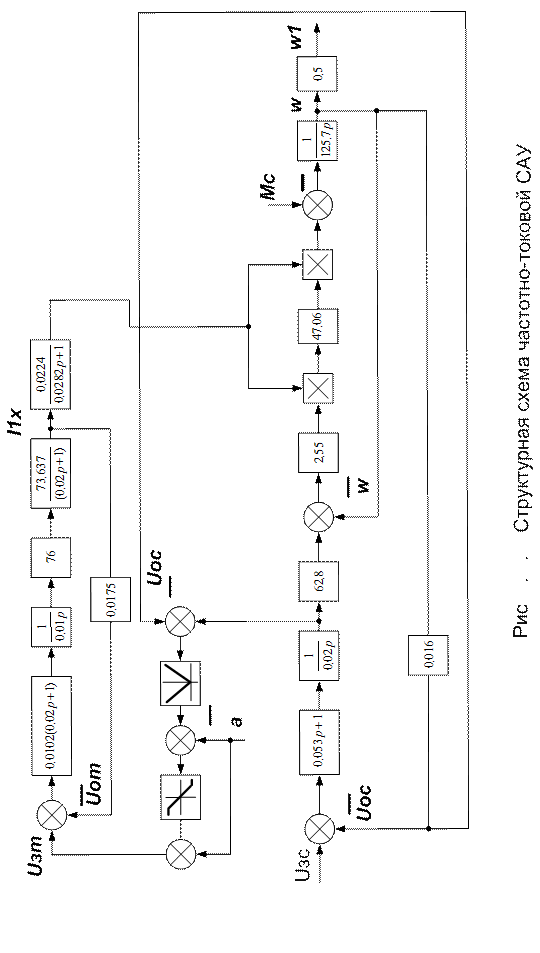
Переходные процессы мы будем строить с помощью программы SMED по структурной схеме, представленной на рис.6.8. По структурной схеме мы будем исследовать переходные процессы  системы управления электроприводом. 

В качестве переходных процессов будем проводить исследование  пуска и разгона электродвигателя до номинальной скорости (рис. 6.9) десятипроцентные скачки напряжения задания скорости (рис. 6.10) и статического момента (рис. 6.11).

.

.

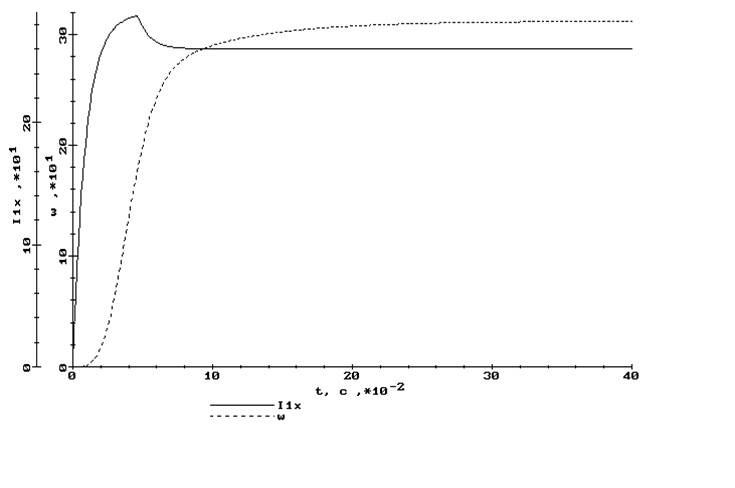
Рис.6.9. Пуск и разгон электродвигателя до номинальной скорости.

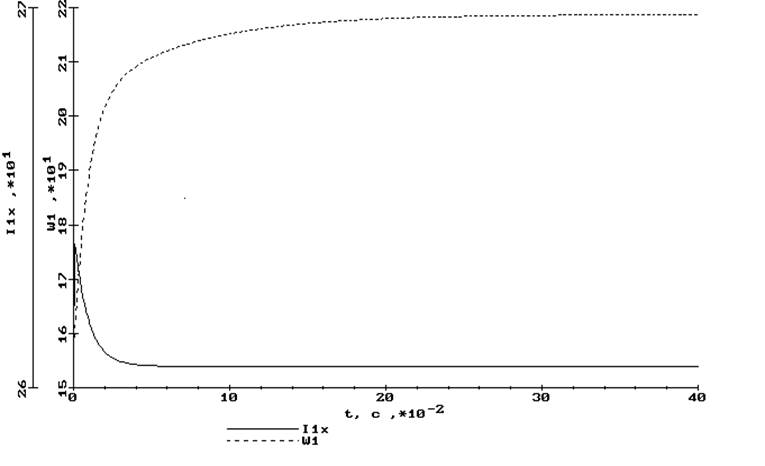
рис.6.10. Скачок задания скорости

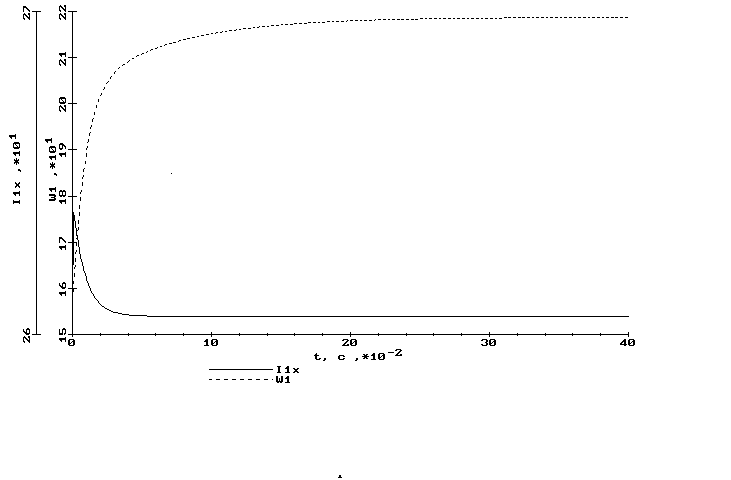
рис.9.11. Скачок статического момента.

Анализируя переходные процессы можно отметить, что ток статора не превышает номинального значения, а в целом характер динамических процессов при пуске удовлетворяет поставленным требованиям. Так как требования по быстродействию не предъявляются то данный показатель не рассматриваем. Скорость при пуске установилась на заданном уровне 154.8 рад/с, что говорит о высокой точности САУ, т.к. пуск осуществляется с нагрузкой.

Скачать файл