



Вопрос 8. Устойчивость.
Причины неустойчивости в инерционности некоторых элементов системы.
В усилителях с ОС с разделительными конденсаторами причина неустойчивости наоборот в форсирующих звеньях.
Применяются алгебраические и частотные методы определения устойчивости. Первые позволяют определять наличие корней с положительной вещественной частью по коэффициентам характеристического уравнения. Вторые методы позволяют судить об устойчивости по частотным характеристикам системы.
Для определения устойчивости системы нужно знать как изменяется выходные и промежуточные величины во времени. В математике такие задачи решаются с помощью диф уравнений. В тау их решают операторным методом, а для компактной записи дин свойств звеньев и всей системы пользуются понятием передаточной функции (это отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях).
Система называется устойчивой, если ошибка ΔХ(t) при t→∞ стремится либо к нулю как в астатической системе либо к конечному значению как в статической системе.
По этому, чтобы исследовать устойчивость САУ надо найти как ошибка изменяется во времени.
Для нахождения изображения ошибки ΔХ(р) пользуются передаточной функцией по ошибке Wδ(p).
Передаточная функция
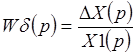
![]()
![]()
![]()
![]()
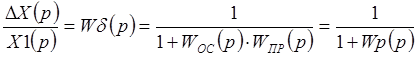
Корни характеристического полинома.
Устойчивость определяется по поведению ошибки во времени при отработки скачка.
Изображение единичного скачка 1/p, тогда
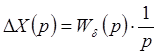
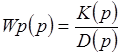
K(p) – полином m – степени
D(p) - полином n – степени
Устойчивость определяется корнями полинома H(p), поэтому H(p) называют характеристическим полиномом, а уравнение H(p)=0 характеристическим уравнением.
Среди n корней всегда можно выделить 3 корня, определяющих вид переходного процесса.
1.
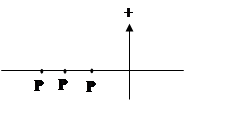
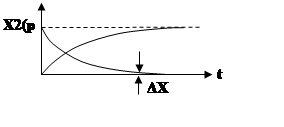
|
2.
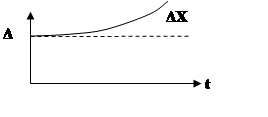
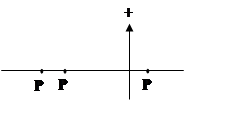
|
3.
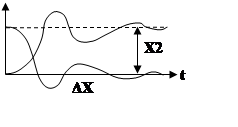
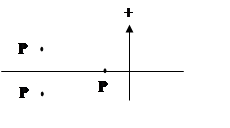
|
4.
|
|
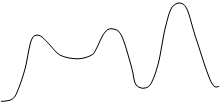
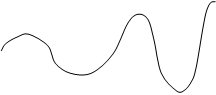
|
|
|
|
|
|
Необходимым условием устойчивости систем любого порядка является положительность коэффициентов характеристического уравнения. Различают достаточные и необходимые критерии устойчивости. Достаточное условие более сильное, т.е. оно выполняется , то система устойчива, а если выполняется необходимое условие, то система может быть как устойчивой, так и не устойчивой. Необходимое условие не выполняется – система не устойчива.
Если хотя бы один коэффициент характеристического уравнения меньше нуля, то система неустойчива.
Доказывают это обычно по теореме Безу: любой полином можно представить в виде произведения 2-х членов, в правой части которых стоит один из корней полинома.
![]()
Вещественные корни, если все корни меньше нуля то скобка больше нуля и при перемножении они дадут положительный коэффициент. Это говорит о том, что в системе не может быть апериодической неустойчивости.
Комплексные корни с положительной вещественной частью: коэффициенты характеристического уравнения могут быть больше нуля, поэтому положительность коэффициентов не может быть достаточным условием, а требует дополнительных исследований.
Частотный критерий устойчивости Михайлова.
Исследуется изменение аргумента H(jw) при изменении частоты 0≤ω<∞
Практически это изменение определяется графически по кривой Михайлова, которая представляет собой годограф H(jw), построенный на комплексной плоскости.
В начале определим чему равно изменение аргумента H(jw) для устойчивой и неустойчивой системы.
Для устойчивой ∆arg H(jw)=n∙π/2 0≤ω<∞
Для неустойчивой ∆arg H(jw)=(n-2m)π/2 0≤ω<∞
|
|
|

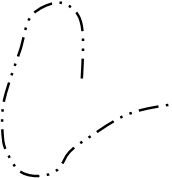

Вывод по критерию Михайлова: Устойчивость исследуется по комплексному числу H(jw) Оно позволяет исследовать устойчивость как замкнутых, так и разомкнутых систем.
Частотный критерий устойчивости Найквиста.
Этот метод был разработан для определения устойчивости усилителей. Этот метод позволяет по АФХ разомкнутого усилителя ( по частотным характеристикам ) определить устойчивость. Этот метод удобен для экспериментального определения устойчивости. Критерий Найквиста позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой. Позволяет исследовать устойчивость только с помощью передаточной функции разомкнутой системы.
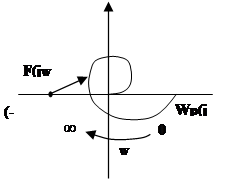
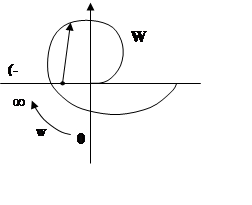
Строится АФХ- годограф комплексного коэффициента передачи, еа комплексной плоскости при изменении 0≤ω<∞.
АФХ строится с помощью алгоритмической формы комплексного числа или с помощью показательной формы комплексного числа.
 |
|||||||
|
|||||||
 |
|||||||
|
|||||||
Таким образом, формулировка критерия Найквиста: если АФХ разомкнутой системы не охватывает точку с координатами (-1; j0), то замкнутая система устойчива, если охватывает то неустойчива. Ежели АФХ проходит через точку (-1), то замкнутая система находится на границе устойчивости.
Физическая трактовка критерия Найквиста: при сдвиге фаз на ПИ ООС превращается в положительную.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.