Широтно-импульсные преобразователи постоянного тока. азначение, принцип действия и классификация широтно-импульсных преобразователей постоянного тока, страница 4

Среднее значение тока нагрузки

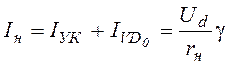, т.е. он не зависит ни от частоты переключений управляемого ключа,  ни от постоянной времени цепи нагрузки, а полностью определяется  средним значением напряжения и активным сопротивлением нагрузки.

1.3.2.  Работа ШИП на двигательную нагрузку

При работе нереверсивного ШИП на якорь двигателя постоянного тока  (рис.  1.5,  а)  возможны  два  режима:  непрерывных  токов  якоря  (рис. 1.5,  б)  и прерывистых токов якоря (рис. 1.5, в).

Основным режимом является режим непрерывных токов (рис. 1.5, б),  для которого изображениями напряжений на нагрузке в период импульса и  паузы будут:

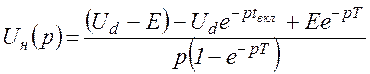       (0<t<t_вкл),

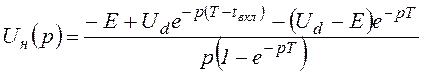     (t_вкл<t<T).

Мгновенные значения тока двигателя

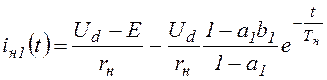        (0<t<t_вкл),

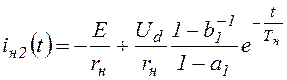          (t_вкл<t<T), где r_н– активное сопротивление якоря двигателя.

Максимальное и минимальное значения тока якоря двигателя:

,   .

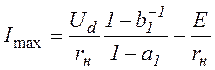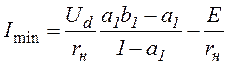Амплитуда пульсаций тока якоря

.

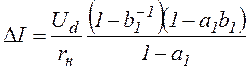Из последнего выражения следует, что амплитуда пульсаций тока  якоря при заданных параметрах цепи нагрузки зависит от времени  включенного состояния и частоты переключений управляемого ключа, уменьшаясь  с  увеличением  частоты  переключений  при  заданномвремени

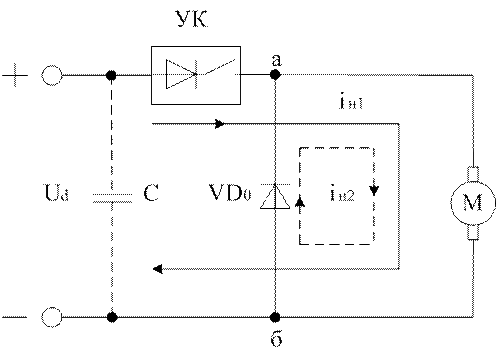
а)

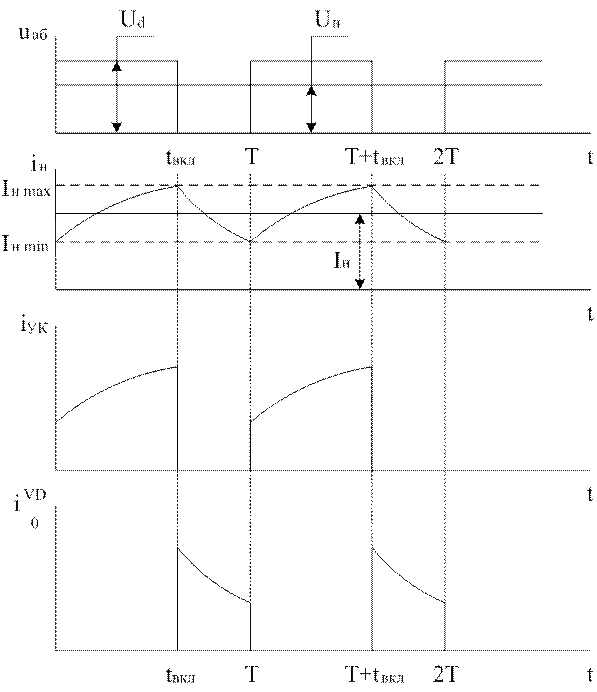
б)

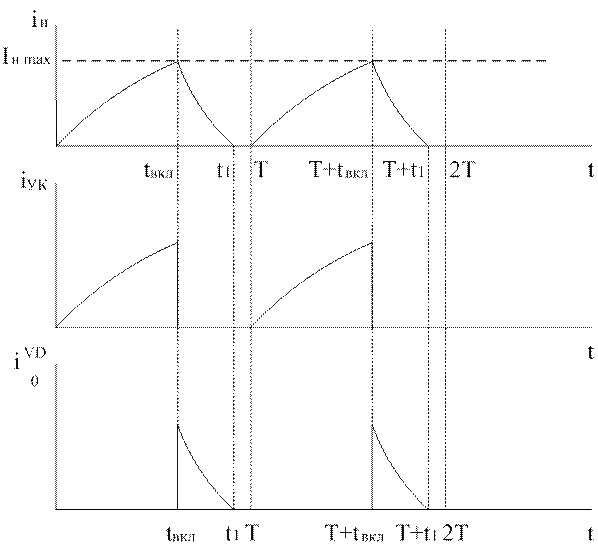
в)

Рис. 1.5.  Схема (а) и временные диаграммы токов и напряжений (б, в) нереверсивного ШИП с двигательной нагрузкой

включенного состояния управляемого ключа.

Среднее значение тока якоря двигателя

.

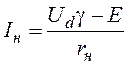Режим прерывистых токов якоря может возникнуть при малых  нагрузках, когда время переключения рабочего ключа соизмеримо с  постоянной времени цепи нагрузки, или при больших значениях противо-э. д. с. (рис. 1.5. в).

Для режима прерывистых токов изображениями напряжений на  нагрузке в период импульса и паузы будут:

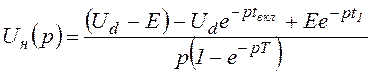          (0<t<t_вкл),

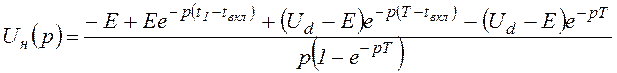  (t_вкл<t<T).

Мгновенные значения тока якоря двигателя:

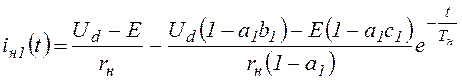   (0<t<t_вкл),       (1.7)

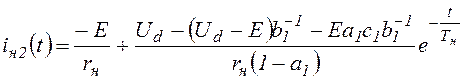   (t_вкл<t<t₁),      (1.8)

где  .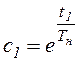

Значение с₁ можно определить, приравняв i_н2(t) нулю при t=t₁-t_вкл:

.

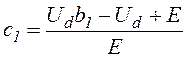Подставляя значение с₁ в (1.7) и (1.8), получаем окончательные  выражения для токов якоря двигателя:

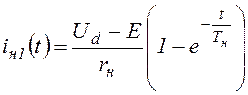     (0<t<t_вкл),

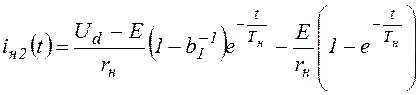    (t_вкл<t<t₁).

Максимальное значение тока якоря двигателя

.

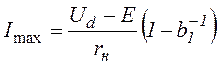Среднее значение тока якоря двигателя

.

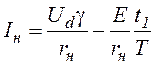Из условия i_н1(t=0)=0 можно найти параметры цепи нагрузки, при  которых наступает граничный режим:

,

.

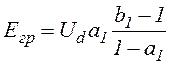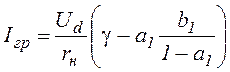1.4.  Основные характеристики ШИП постоянного тока

На рис. 1.6 показаны внешние характеристики нереверсивных ШИП без режима торможения (рис. 1.6, а) и с режимом торможения (рис. 1.6, б).

В ШИП внутренняя координата g делит ШИП на две части – ШИМ и УК, управляющие свойства которых определяются характеристиками управления g=j_У(U_У) для ШИМ и E_d=j_УК(g) для управляющего ключа. Результирующая  характеристика  управления  ШИП  находится  как  сложная функция E_d=j_УК[j_У(U_У)]=j(U_У). Опорное напряжение, определяющее характеристику j_У(U_У), должно иметь пилообразную линейную форму:

для нереверсивного ШИП

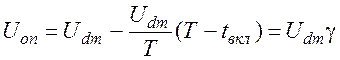;          (1.9)

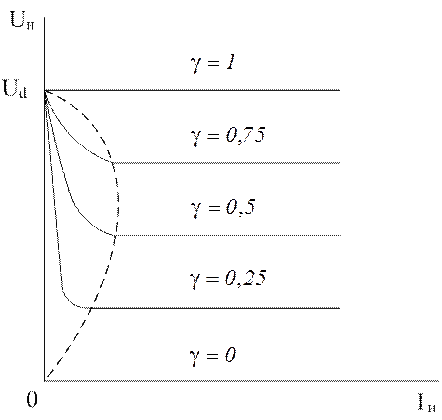
а)

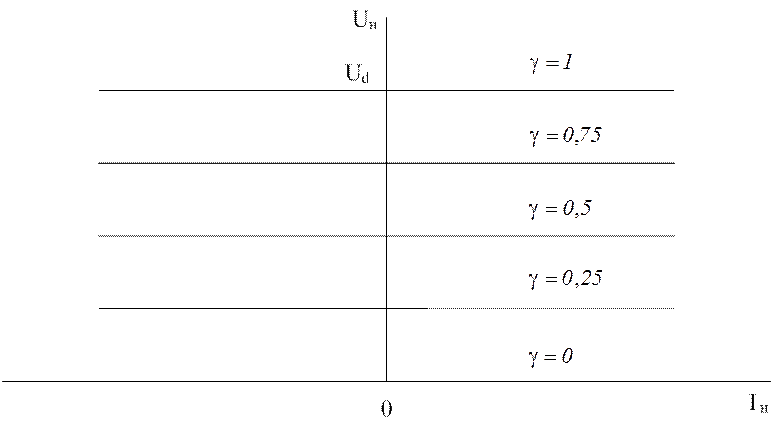
б)

Рис. 1.6. Внешние характеристики нереверсивного ШИП без режима торможения (а) и с режимом торможения (б)

для реверсивного ШИП с разнополярными импульсами

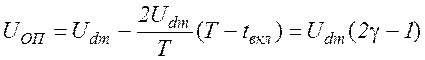.         (1.10)

Так как начало положительного импульса соответствует условию U_У=U_ОП, то характеристики управления ШИМ определятся как функции, обратные (1.9) и (1.10):

g= U_У/U_dm;                       (1.11)

g=(1+ U_У/U_dm)/2.              (1.12)

Подстановка (1.11) в (1.1), а (1.12) в (1.2) даст выражение для результирующей характеристики управления ШИП:

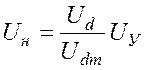.             (1.13)

При U_У=U_dm g=1 и U_н=U_нmax=U_d. Однако коммутация вентилей происходит не мгновенно, а занимает некоторый интервал времени. Поэтому практически g_max<1 и устанавливается с помощью системы управления на уровне 0,85—0,90, которому соответствует U_нmax=(0,7¸0,9)U_d.