При открывании управляемого ключа в цепи нагрузки протекает ток (на рис. 1.4, а) путь тока показан сплошной линией), При закрывании управляемого ключа ток нагрузки за счет э. д. с. самоиндукции сохраняет свое прежнее направление, замыкаясь через обратный диод Д0 (путь тока показан пунктирной линией).
Для защиты ключа от перенапряжения, возникающего при разрывах цепи питания, на входе ШИП устанавливают фильтр, выходным звеном которого является конденсатор С (на рис. 1.4, а) показан пунктиром).
Мгновенные значения тока нагрузки во время импульса и паузы можно определить, например, методом отдельных составляющих, использующим непрерывное преобразование Лапласа. Известно, что если оригинал u(t) есть периодическая функция с периодом T, то соответствующим изображением будет
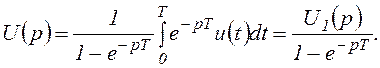
Здесь U1(p)- изображение функции u1(p), которая совпадаете с функцией u(t) на протяжении первого периода и равна нулю при t<0.
В общем случае установившаяся реакция цепи может быть определена по двум составляющим: переходной и свободной:
![]() .
.
Свободную составляющую тока определяют
как сумму вычетов подынтегральной функции относительно полюсов
функции 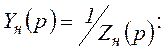
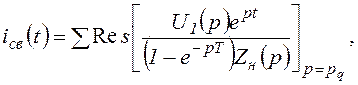
где полюсы pq находят из условия Zн(p)=0. Это условие дает конечное число полюсов. Поэтому число слагаемых в выражении для iсв(t) будет также конечным и выражение свободного тока получается в замкнутой форме.
Преобразуем
выражение 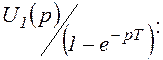
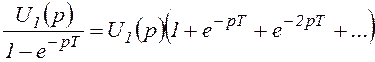 .
.
Если рассматривается решение только в течение первого периода, т. е. 0<t<T, то изображением воздействующей э. д. с. будет U1(t).
Эта особенность позволяет определить изображение переходного тока на протяжении периода в виде
![]() .
.
Согласно теореме Коши о вычетах переходный ток
![]()
где полюсы pq находят как полюсы функции U1(p)Yн(p).
Число полюсов оказывается конечным, поэтому выражение для переходного тока на протяжении первого периода iпер1(t) получается в замкнутой форме.
Используя выражения для iсв1(t) и iпер1(t), определяющие в замкнутой форме переходный и свободный токи в течение первого периода, можно определить в замкнутой форме и установившийся (квазиустановившийся) ток на этом интервале:
![]() .
.
Если кривая воздействующего напряжения u(t) симметрична относительно оси абсцисс, то аналогично можно определить установившийся ток на протяжении полупериода. Если же эта кривая в течение полупериода имеет несколько характерных участков, для которых воздействующая функция может выражаться определенной аналитической зависимостью, то указанную особенность можно распространить и на интервалы периода.
Изображение напряжения, действующего в схеме рис. 1.4, а,
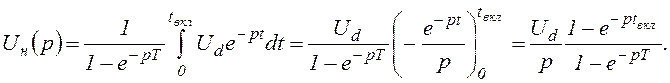
Изображение тока нагрузки
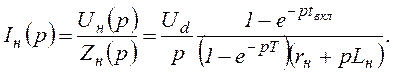
Свободный ток
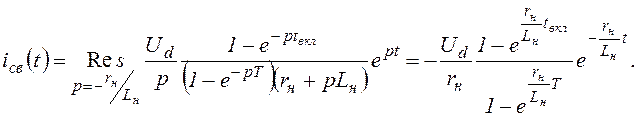
Переходный ток на интервале 0<t<tвкл
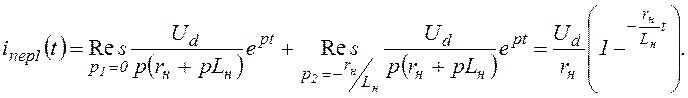
Искомый установившийся ток на интервале 0<t<tвкл
![]()
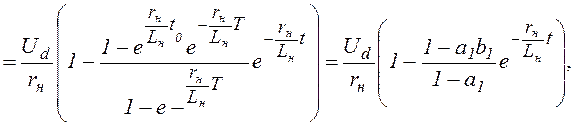 (1.4)
(1.4)
где 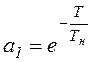 ;
; 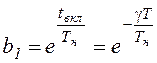 ;
; 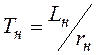 -постоянная времени цепи
нагрузки.
-постоянная времени цепи
нагрузки.
Для нахождения тока на интервале tвкл<t<Tначало координат необходимо сдвинуть вправо на величину tвкл. Тогда изображение напряжения на нагрузке запишется в виде
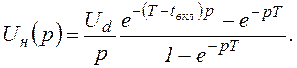
Свободный, переходный и установившийся токи на интервале tвкл<t<T определяются соответственно выражениями:
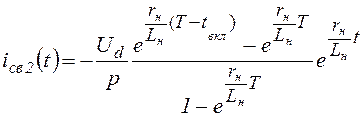 ,
,
![]()
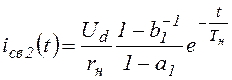 . (1.5)
. (1.5)
Максимальное и минимальное значения тока нагрузки (тока через управляемый ключ и обратный диод) можно найти из выражений (1.4), (1.5) при подстановке t=tвкли t=T-tвкл:
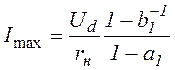 ,
, 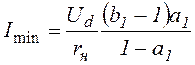 .
.
Амплитуда пульсаций тока нагрузки
 . (1.6)
. (1.6)
Из выражения (1.6) следует, что амплитуда пульсаций тока нагрузки максимальна при g=0,5, т. е.
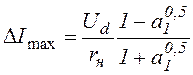 .
.
Коэффициент пульсаций выходного напряжения
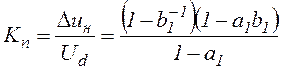 .
.
Токи через
управляемый ключ и обратный диод протекают соответственно на интервалах ![]() и
и ![]() .
Интегрируя токи на соответствующих интервалах, определим среднее значение
токов управляемого ключа и обратного диода:
.
Интегрируя токи на соответствующих интервалах, определим среднее значение
токов управляемого ключа и обратного диода:
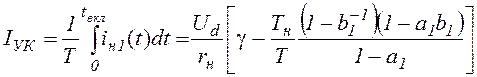 ,
,
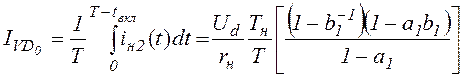 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.