11. Временные и частотные (ЛЧХ) характеристики типовых звеньев. САУ.
1. Пропорциональное (или безынерционное) звено.
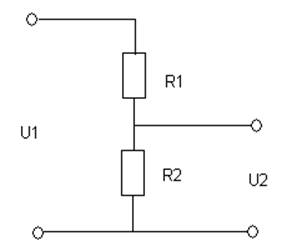 W(p)=R1/(R1+R2)=K; W(jω)=K; φ(ω)=0; W(ω)=K
W(p)=R1/(R1+R2)=K; W(jω)=K; φ(ω)=0; W(ω)=K
h(p)=W(p)*1/p=W(p)/p=K/p
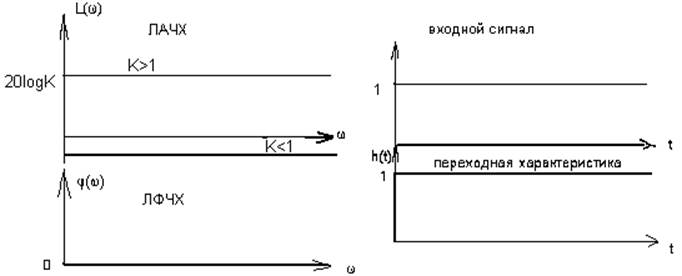
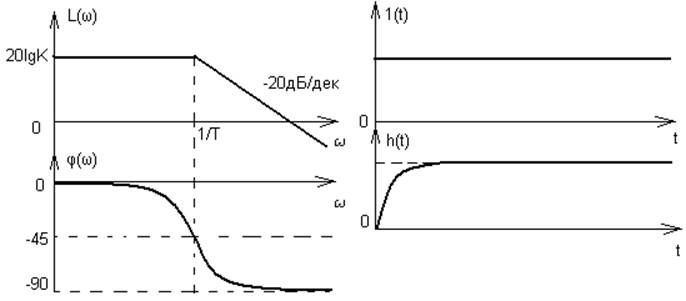
h(t) – переходная характеристика;
L(ω) – ЛАЧХ;
φ(ω) – ЛФЧХ;
Для активных звеньев (с ОУ) К может быть больше 1, тогда L(ω) будет лежать выше нуля. Для пассивного звена, которое изображено на рисунке, L(ω) лежит ниже нуля.
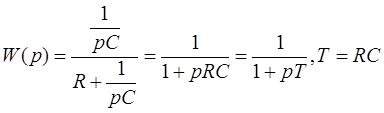 |
 2. Инерционное звено.
2. Инерционное звено.
Для второй схемы T=L/R.
В общем случае звено данного типа имеет W(p) следующего вида:
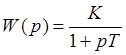 |
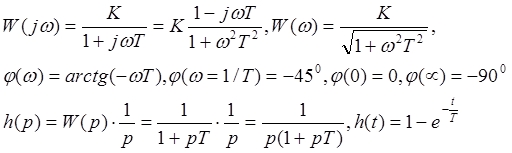 |
 |
![]()
3. Интегрирующее звено.
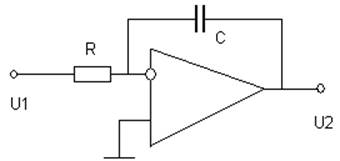 W(p)=-U2(p)/U1(p)=-1/pRC=-1/Tu, Tu=RC.
W(p)=-U2(p)/U1(p)=-1/pRC=-1/Tu, Tu=RC.
h(p)=W(p)/p=1/p2Tu. h(t)=t/Tu.
W(jω)=1/jωTu, W(ω)=1/ωTu,
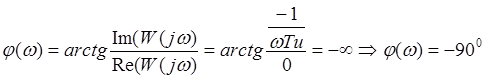

Ku=1/Tu.
Tu показывает, за какое время выходная величина изменится на единицу времени.
Ku – скорость изменения выходной величины, т. е. показывает, насколько изменится выходная величина за единицу времени.
Интегрирующее звено наз-ся непозиционным звеном, т. к. на выходе устанавливается скорость изменения вых. величины.
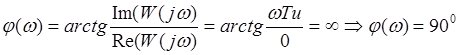 |
W(p)=pRC=pT, где Т=RC. W(jω)= jωT, W(ω)=ωT.
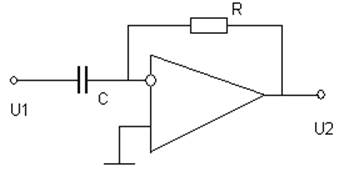 h(p)=W(p)/p=pT/p=T.
h(p)=W(p)/p=pT/p=T.
Реакцию на единичный скачок такого звена определим при помощи теоремы о начальном и конечном значении функции:
Реакцией на единичный скачок такого звена является так называемая δ-функция (дельта-функция)
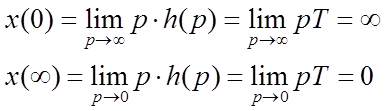 |
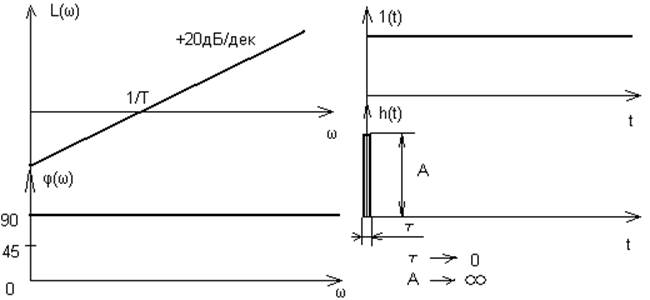
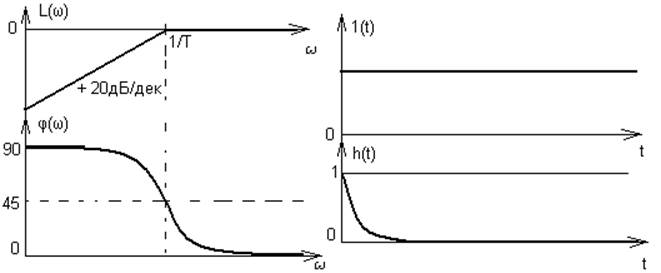
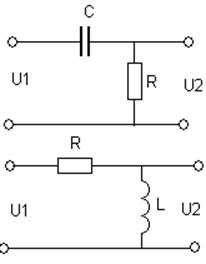
5. Реально-дифференцирующее звено.
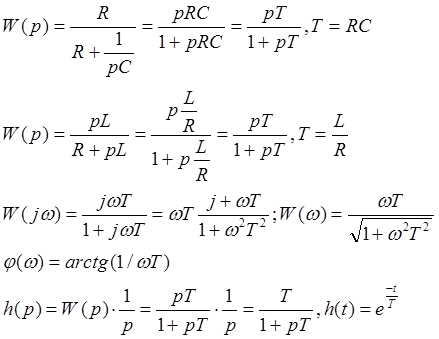 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.