МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ИМЕНИ П.О.СУХОГО
Факультет автоматизированных и информационных систем
Кафедра «Автоматизированный электропривод»
Лабораторная работа №2
по моделированию в электроприводах
«Моделирование электродвигателя постоянного тока последовательного возбуждения »
Исполнитель: студент гр. ЭП-31
Руководитель: преподаватель
Гомель, 2005
Лабораторная работа №2
Моделирование электродвигателя постоянного тока последовательного возбуждения
Цель работы
· закрепить полученные практические навыки составления программ моделирования;
· исследовать динамические свойства двигателей постоянного тока.
Задание
В данной работе необходимо составить программу моделирования по системе дифференциальных уравнений двигателя постоянного тока последовательного возбуждения с учетом кривой намагничивания и рассчитать переходные процессы при:
1. Пуске под нагрузкой (0.5 · MН).
2. Набросе нагрузки (до MН).
3. Торможении.
По результатам расчетов необходимо построить:
1. В одних осях диаграммы тока и скорости.
2. Динамическую механическую характеристику (по оси абсцисс - ток, по оси ординат - скорость).
Двигатель – Д31, тихоходное исполнение.
Метод решения дифференциальных уравнений – Башарина.
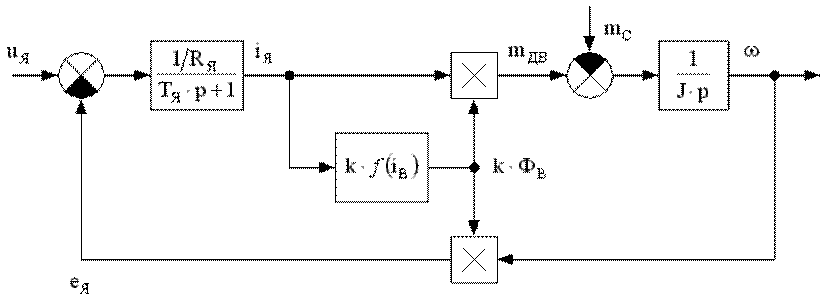
Рис. 1. Структурная схема двигателя постоянного тока последовательного возбуждения без учета фиктивной обмотки вихревых токов.
На рис. 1 обозначено:
uЯ - напряжение на якорной цепи двигателя;
еЯ - ЭДС якоря;
iЯ - ток якоря двигателя;
k · ФВ - произведение конструктивной постоянной двигателя на поток возбуждения;
f(iВ) - функция, отражающая нелинейную зависимость потока возбуждения от тока обмотки возбуждения (для ДПТ ПВ iЯ = iВ);
mДВ - момент двигателя;
mC - момент сопротивления;
ω - угловая скорость вращения двигателя;
RЯ и TЯ - сопротивление и постоянная времени якорной цепи;
J - момент инерции якоря.
Кривую намагничивания для двигателей серии Д можно аппроксимировать кусочно-линейной функцией, представленной на рис. 2.
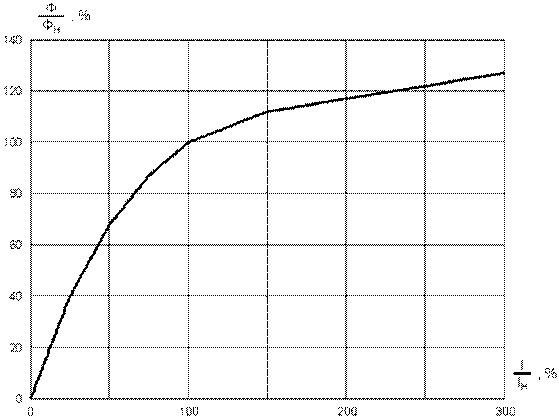
Рис. 2. Кусочно-линейная функция
По осям отложены относительные значения тока и потока двигателя (отнесенные к номинальным значениям). Координаты конечных точек отрезков:
(0%; 0%). (75%; 87%).
(25%; 40%). (100%; 100%).
(50%; 68%). (150%; 112%).
Последний участок характеристики - луч проходящий через точку (250%; 122%).
Порядок выполнения работы
1. В соответствии со схемой модели (рис. 1) составляем систему дифференциальных уравнений.
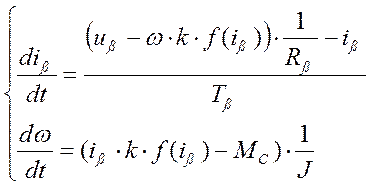 (1)
(1)
2. Используя справочные данные, определяем параметры заданного двигателя и заносим и в таблицу 1.
Таблица 1
|
Тип дви-гате- ля |
Число активных провод-ников якоря, N |
Число парал-лельных ветвей якоря, 2a |
Сопротивление якоря и добавочных полюсов, Ом |
Магнитный поток на полюс, режим ПВ =40 %, 10-2 Вб |
Напря- жение якоря, В |
Мощность при ПВ = 40 %, кВт |
|
Д31 |
738 |
2 |
0,42 |
0,86 |
220 |
8 |
Продолжение таблицы 1
|
Номи- наль-ный ток, А |
Номинальная частота вращения, об/мин |
Число пар главных полюсов |
Число пар добавоч- ных полюсов |
βК для компен-сирован. машин |
LЯ, мГн |
ТЯ, мс |
k |
МН, Н∙м |
|
47 |
800 |
2 |
2 |
0,2 |
5,6 |
13,3 |
235 |
95,6 |
Остальные параметры находим из формул и также заносим в таблицу 1.
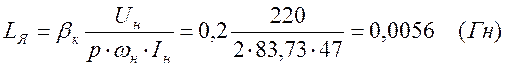 |
где 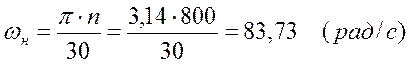
Постоянная времени якорной цепи: 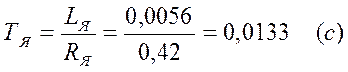
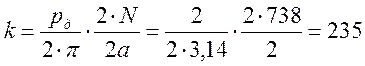 |
Конструктивная постоянная двигателя:
Номинальный момент нагрузки:
![]()
3. Программа моделирования по системе уравнений в соответствии с заданным методом численного решения систем дифференциальных уравнений и составленной системой уравнений.
Program Laba2;
{Лабораторная работа N2.Выполнил студент гр. ЭП-31
, метод Башарина}
Type
DArray = array [1..10] of double;
DMatrix = array [1..10, 1..10] of double;
{Определение значений входных воздействий}
Procedure pX(Uj, Mn, tt: double; var X: DArray);
begin
{x1 - скачок или сброс напряжения на якоре;
х2 - значение момента сопротивления}
if (tt>0) and (tt<0.4) then X[1] := Uj else X[1] := 0;
if tt>0 then
if tt<0.2 then X[2]:=0.5*Mn else X[2]:=Mn
else X[2]:=0
end;
Function Sign(x:double):double;
begin
if x>0 then Sign:=1 else
if x<0 then Sign:=-1 else
Sign:=0;
end;
{Определение значения функции f(iя)}
Function Flux(Iv, Inag, Fn: double):double;
var
f:double; {Фо}
i1:double; {iво}
begin
i1:=abs(Iv)/Inag;
if i1<=0.25 then f:=0.4*i1/0.25 else
if i1<=0.5 then f:=0.4+0.28*(i1-0.25)/0.25 else
if i1<=0.75 then f:=0.68+0.19*(i1-0.5)/0.25 else
if i1<=1 then f:=0.87+0.13*(i1-0.75)/0.25 else
if i1<=1.5 then f:=1+0.12*(i1-1)/0.5 else f:=1.12+0.1*(i1-1.5);
Flux:=f*Fn*Sign(i1)
end;
{Расчет алгебраических уравнений и определение значений правых частей дифференциальных уравнений}
Procedure pF(Y: DMatrix; Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tt: double;
It: integer; var F: DArray);
var
x: DArray;
begin
{Расчет значений входных воздействий}
pX(Uj, Mn, tt, X);
{Правая часть диф. уравнений для угловой скорости}
F[1] := (Y[2,It]*K*Flux(Y[2,It],Inag,Fn)-X[2])*Jj ;
{Правая часть диф. уравнения для тока якоря}
F[2] := (X[1]-Y[1,It]*K*Flux(Y[2,It],Inag,Fn)/Rj-Y[2,It])/Tj;
end;
{Определение значений переменных модели на текущем шаге
(метод Башарина)}
Procedure pY(Yp: DMatrix; Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tt, dt: double;
It: integer; var Y: DMatrix);
var
F: DArray;
i, j: integer;
begin
{Расчет алгебраических уравнений и значений правых частей диф. уравнений}
pF(Yp, Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tt-dt, It, F);
{Первая итерация - метод Эйлера}
for i := 1 to 2 do
{Yn+1(1) = Yn + dt*fn}
Y[i,1] := Yp[i,It] + dt*F[i];
{Цикл по остальным итерациям - от 2-ой до последней - It}
for j := 2 to It do
begin
{Подготовка значений (Yn + Yn+1(v))/2}
for i := 1 to 2 do
Y[i,j] := (Yp[i,It] + Y[i,j-1])/2;
{Расчет алг. уравнений и правых частей диф. уравнений f( (Yn + Yn+1(v))/2, Xn+0.5 )}
pF(Y, Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tt-dt/2, j, F);
{Расчет переменных модели на текущем шаге для текущей итерации}
for i := 1 to 2 do
{Yn+1(v+1) = Yn + dt*f(...)}
Y[i,j] := Yp[i,It] + dt*F[i];
end;
end;
{Ввод исходных данных}
Procedure pIn( var Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tk, dt: double;
var It: integer; var filename: string);
var
f: text;
begin
write('Введите имя файла ввода ');
readln(filename);
assign(f, filename);
reset(f);
write('Введите имя файла вывода ');
readln(f, filename);
write('Введите значение напряжения на якоре Uя ');
readln(f, Uj);
write('Введите значение номинального момента Мн ');
readln(f, Mn);
write('Введите значение сопротивления якорной цепи Rя ');
readln(f, Rj);
write('Введите значение пост. времени якорной цепи Tя ');
readln(f, Tj);
write('Введите значение конструктивной пост. двигателя K ');
readln(f, K);
write('Введите значение момента инерции якоря J ');
readln(f, Jj);
write('Введите значение тока нагрузки Iн ');
readln(f, Inag);
write('Введите значение магнитного потока Фн ');
readln(f, Fn);
write('Введите интервал расчета t ');
readln(f, tk);
write('Введите шаг расчета dt ');
readln(f, dt);
write('Введите количество итераций ');
readln(f, It);
close(f);
end;
Var
Y, Yp: DMatrix;
Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tk, dt, tt: double;
i, It, N: integer;
f: text;
filename: string;
Begin
{Ввод исходных данных}
pIn(Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tk, dt, It, filename);
{Открытие файла для вывода значений}
assign(f, filename);
rewrite(f);
{Начальные условия - нулевые}
fillchar(Y, sizeof(Y), 0);
fillchar(Yp, sizeof(Yp), 0);
tt := 0;
{Выводим значения в момент времени t=0}
writeln(f, tt:13:5, Y[1,It]:16:5, Y[2,It]:16:5);
{Определение кол-ва шагов расчета}
N := round(tk/dt);
{Цикл по шагам расчета}
for i := 1 to N do
begin
{Текущее время (на текущем шаге)}
tt := dt*i;
{Определяем значения переменных на текущем шаге}
pY(Yp, Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tt, dt, It, Y);
{Вывод рассчитанных значений}
writeln(f, tt:13:5, Y[1,It]:16:5, Y[2,It]:16:5);
{Перенос значений на шаг назад}
Yp := Y;
end;
{Закрытие файла вывода}
close(f);
End.
Используя заданные параметры входных воздействий и звеньев модели, с помощью составленной программы рассчитываем переходной процесс.
Строим в программе MathCAD диаграммы переходных процессов.
Сначала построим в одних осях диаграммы тока и скорости.
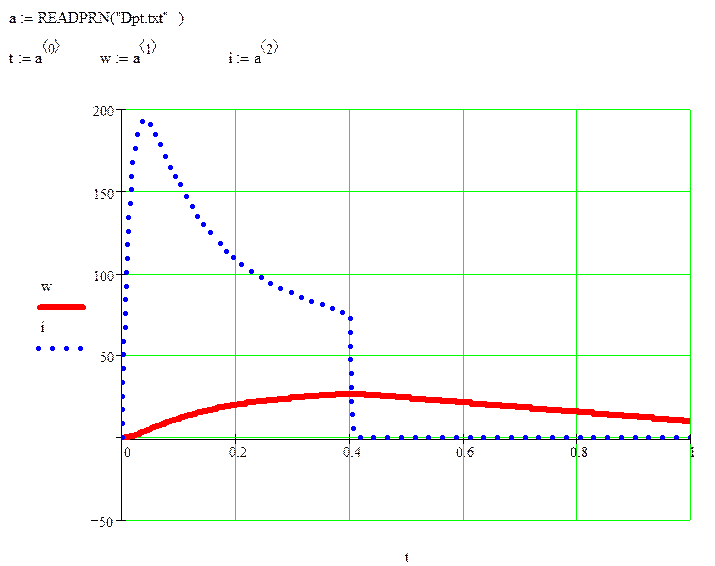
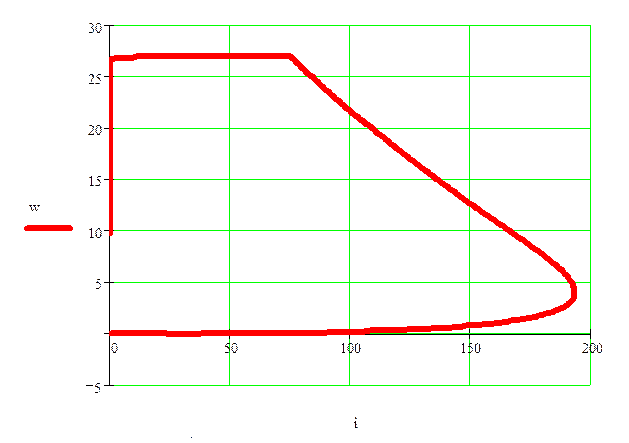
А теперь - динамическую механическую характеристику (по оси абсцисс - ток, по оси ординат - скорость).
4. Составим таблицу переменных для программы.
Таблица соответствия переменных
|
Название переменной |
Назначение |
|
Программа |
|
|
Y, Yp |
Значения переменных модели, для которых есть дифференциальные уравнения, на текущем и предыдущем шагах расчета, соответственно |
|
Mn, Rj, Tj, K, Jj, In |
Параметры звеньев: номинальный момент на якоре, сопротивление якоря, постоянная времени якорной цепи, конструктивная постоянная двигателя, момент инерции якоря |
|
Inag, Fn |
Параметры функции f(iВ), входящей в звено на схеме: номинальный ток якоря; магнитный поток на полюс |
|
Uj |
Параметры входных переменных: величина скачка напряжения якоря (амплитуда) |
|
tk, dt, tt |
Интервал и шаг расчета, текущее время |
|
It |
Количество итераций |
|
i |
Счетчик шагов расчета |
|
N |
Количество шагов расчета |
|
f |
Файл вывода |
|
Filename |
Имя файла вывода |
|
Процедура ввода исходных данных pIn |
|
|
Uj, Mn, Rj, Tj, K, Jj, In, Inag, Fn, tk, dt, Filename |
То же, что и в программе |
|
f |
Файл ввода |
|
Процедура расчета значений переменных модели pY |
|
|
Yp, Uj, Mn, Rj, Tj, K, Jj, Inag, Fn, tt, dt, It, Y |
То же, что и в программе |
|
F |
Рассчитываемые значения правых частей дифференциальных уравнений |
|
i |
Счетчик дифференциальных уравнений |
|
j |
Счётчик итераций |
|
Процедура расчета алгебраических уравнений и правых частей | |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.