Практическая работа № 7
Распределение напряжений под действием равномерно распределенной нагрузки
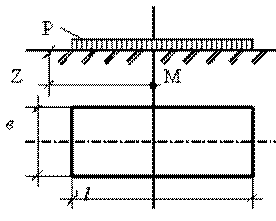 Для определения
вертикальных напряжений возникающих по оси z, проходящей через центр загруженной
прямоугольной площадки используется формула σz =α⋅P
Для определения
вертикальных напряжений возникающих по оси z, проходящей через центр загруженной
прямоугольной площадки используется формула σz =α⋅P
где Р – давление на основание
α - коэффициент распределения
в горной породе напряжений, зависящий от соотноl 2z шения n =![]() и m =
и m =
![]() . b b
. b b
Значение этого коэффициента приведены в
таблице 1. Рисунок 1
Для определения вертикальных напряжений возникающих по оси z, проходящей через углы загруженного прямоугольника используется формула σz =α′⋅P
где Р – давление на основание
α′ - коэффициент распределения напряжений по глубине основания.
Значение коэффициента α′ можно получить из таблицы 2, принимая α′ =α/4,
значение α
будет зависеть от двух параметров n =![]() и m=
и m= ![]() .
.
Это решение положено в основу метода угловых точек.Суть этого метода состоит в том, что если загруженную площадку разбить на прямоугольники, то напряжения в точке, которая является общей для всех прямоугольников, равны сумме напряжений, возникающих в этой точке от действия каждого из загруженных прямоугольников. Площадку, разбивают на прямоугольники таким образом, чтобы точка, в которой рассчитываются напряжения, была угловой и общей для этих прямоугольников.
Возможны два основных случая расположения точки относительно загруженной площадки: внутри ее контура и за ее пределами.
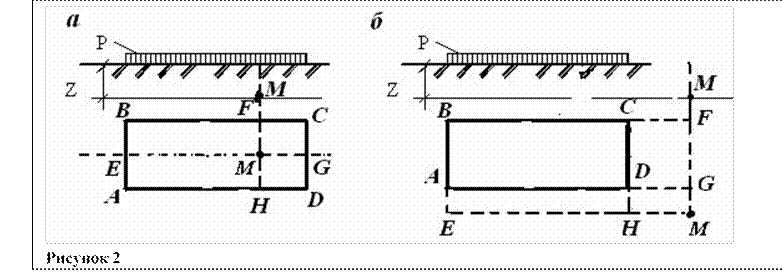
В первом случае (рис. 2а) напряжение в точке М определяется как сумма угловых напряжений от действия нагрузки по четырем прямоугольникам AEMH, HMGD, EMFB и MFCG, а именно: σЯ = (α1′ +α2′ +α3′ +α4′)⋅ Р где α′1, α′2, α′3, α′4 – коэффициенты, определяемые в зависимости от соотношения сторон четырех прямоугольников.
В первом случае (рис. 2б) напряжение в точке М будет определяется следующим образом σЯ = (α1′ −α2′ −α3′ +α4′ )⋅ Р где α′1 – коэффициент, определяемый в зависимости от соотношения сторон
прямоугольника EBFM; α′2, – для прямоугольника AEGM; α′3, – для прямоугольника HCFM; α′2, – для прямоугольника HDGM;
Если при определении коэффициента αпо таблице соотношения m и n между строк и столбцов таблицы, то αопределяется путем интерполяции. Суть метода интерполяции состоит в следующем:
1. Если расчетная точка по своим координатам (m и n) попадает между строк и столбцов таблицы (рис. 3), то значение коэффициента αопределяется по формуле
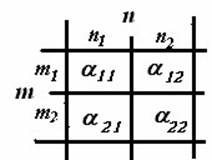 α=α11 −x1 +y ,
α=α11 −x1 +y ,
(m − m1) (⋅ α11 −α21)
x1 = ![]() ,
,
m2 − m1
(m − m1) (⋅ α12 −α22)
x2 = ![]() ,
,
m2 − m1
(n
−
n1) (⋅ α12 − x2 −α11+x1) Рисунок 3 Схема поясняющая y = ![]() .
.
n2 − n1 способ интерполяции
2. Если расчетная точка по своим координатам
(m и n) находится в столбце таблицы, то расчетные формулы упрощаются: α=α11 − х1.
3. Если расчетная точка по своим координатам (m и n) находится в строке таблицы, то расчетные формулы примут вид:
α=α11 − у1,
(n −
n1) (⋅ α12 −α11) где y = ![]() .
.
n2 − n1
Задание
В соответствии с исходными данными (таблица 1) необходимо определить вертикальные напряжения в горном массиве на глубине 2 м от поверхности. На основание передается равномерно распределенная нагрузка Р=300000 н/м2. Значение σZ в расчетных точках представит в МПа.
Контрольные вопросы
4. Сущность метода угловых точек
5. Как зависят сжимающие напряжения от площади загрузки.
6. Как найти сжимающие напряжения в точке находящейся на контуре прямоугольника давления.
7. Как найти сжимающие напряжения в точке находящейся вне прямоугольника давления.
8. Как найти сжимающие напряжения в точке находящейся в нутрии прямоугольника давления.
Таблица 1 Исходные данные для расчетов
|
№ Вари- анта |
Размеры фундамента, м |
Координаты расчетных точек, м |
№ Вари- анта |
Размеры фундамента, м |
Координаты расчетных точек, м |
||||||||||||
|
Точка 1 |
Точка 2 |
Точка 3 |
Точка 1 |
Точка 2 |
Точка 3 |
||||||||||||
|
a |
b |
х |
у |
х |
у |
х |
у |
a |
b |
х |
у |
х |
у |
х |
у |
||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
2,4 2,6 2,6 1,8 2,4 2,6 2,4 2,3 2,2 2,0 1,9 2,6 2,5 2,9 4,0 |
1,6 1,0 1,2 0,8 1,2 1,4 1,4 1,3 1,4 1,5 1,7 2,0 1,0 1,4 2,0 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
1,2 1,3 1,3 0,9 1,2 1,3 1,2 1,65 1,1 1,0 0,95 1,3 1,25 1,45 2,0 |
0,8 0,5 0,6 0.4 0,6 0,7 0,7 0,65 0,7 0,75 0,85 1,0 0,5 0,7 1.0 |
2,5 2,6 2,4 2,0 1,8 2,3 2,0 2,0 1,7 2,0 2,1 1,5 1,55 1,9 3,0 |
1,6 1,8 2,1 0,9 1,6 2,5 2,0 0,8 0,9 1,3 1,6 2,0 0,8 2,1 2,0 |
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
3,5 2,4 2,8 2,7 2,5 2,6 2,7 2,0 2,2 1,8 3,0 3,0 3,0 2,4 2,3 |
1,7 1,3 1,4 1,5 1,3 1,3 1,3 1,0 1,2 1,2 1,4 1,2 1,0 1,8 1,8 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
1,75 1,2 1,4 1,35 1,25 1,3 1,35 1,0 1,1 0,9 1,5 1,5 1,5 1,2 1,15 |
0,85 0,65 0,7 0,75 0,65 0,65 0,65 0,5 0,6 0,6 0,7 0,6 0,5 0,9 0,9 |
2,0 1,8 2,0 1,4 1,8 1,8 2,0 2,1 2,5 1,9 2,0 2,1 2,7 2,9 3,0 |
1,5 1,6 2,0 1,5 1,6 1,6 2,0 2,3 3,5 1,7 1,5 0,9 2,7 1,3 2,3 |
Таблица 2 Значения коэффициента α
|
Коэффициент αдля фундаментов |
|||||||||||||||
|
т |
прямоугольных с отношением сторон n=l/b |
ленточных (п ≥10) |
|||||||||||||
|
круглых |
|||||||||||||||
|
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,4 |
2,8 |
3,2 |
4 |
5 |
|||||
|
0,1 0,4 0,8 1,2 1,6- 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8 5,2 5,6 6,0 6,4 6,8 7,2 7,6 8,0 8,4 8,8 9,2 9,6 10 11 12 |
1,000 0,949 0,756 0,547 0,390 0,285 0,214 0,165 0,130 0,106 0,087 0,073 0,062 0,053 0,046 0,040 0,036 0,032 0,028 0,024 0,022 0,021 0,019 0,018 0,016 0,015 0,011 0,009 |
1,000 0,960 0,800 0,606 0,449 0,336 0,257 0,201 0,160 0,130 0,108 0,091 0,077 0,066 0,058 0,051 0,045 0,040 0,036 0,032 0,029 0,026 0,024 0,022 0,020 0,019 0,017 0,015 |
1,000 0,968 0,830 0,652 0,496 0,379 0,294 0,232 0,187 0,153 0,127 0,107 0,092 0,079 0,069 0,060 0,053 0,048 0,042 0,038 0,035 0,032 0,029 0,026 0,024 0,022 0,020 0,018 |
1,000 0,972 0,848 0,682 0,532 0,414 0,325 0,260 0,210 0,173 0,145 0,122 0,105 0,091 0,079 0,070 0,062 0,055 0,049 0,044 0,040 0,037 0,034 0,031 0,028 0,026 0,023 0,020 |
1,000 0,974 0,859 0,703 0,558 0,441 0,352 0,284 0,232 0,192 0,161 0,137 0,118 0,102 0,089 0,078 0,070 0,062 0,056 0,050 0,046 0,042 0,038 0,035 0,032 0,030 0,027 0,024 |
1,000 0,975 0,866 0,717 0,578 0,463 0,374 0,304 0,251 0,209 0,176 0,150 0,130 0,112 0,099 0,087 0,077 0,069 0,062 0,056 0,051 0,046 0,042 0,039 0,036 0,033 0,029 0,026 |
1,000 0,976 0,870 0,727 0,593 0,481 0,392 0,321 0,267 0,224 0,190 0,163 0,141 0,123 0,108 0,095 0,085 0,076 0,068 0,062 0,056 0,051 0,047 0,043 0,040 0,037 0,033 0,028 |
1,000 0,976 0,875 0,740 0,612 0,505 0,419 0,350 0,294 0,250 0,214 0,185 0,161 0,141 0,124 0,110 0,098 0,088 0,080 0,072 0,066 0,060 0,055 0,051 0,047 0,044 0,040 0,034 |
1,000 0,977 0,878 0,746 0,623 0,520 0,437 0,369 0,314 0,270 0,233 0,203 0,178 0,157 0.139 0,124 0,111 0,100 0,090 0,082 0,075 0,069 0,063 0,058 0,054 0,050 0,044 0,038 |
1,000 0,977 0,879 0,749 0.630 0,529 0,449 0,383 0,329 0,285 0,248 0,218 0,192 0,170 0,152 0,136 0,122 0,110 0,100 0,091 0,084 0,077 0,070 0,065 0,060 0,056 0,050 0,044 |
1,000 0,977 0,880 0,753 0,636 0,540 0,462 0,400 0,348 0,305 0,270 0,239 0,213 0,191 0,172 0,155 0,141 0.128 0,117 0,107 0,098 0,091 0,084 0,078 0.072 0, 067 0,060 0,051 |
1,000 0,977 0,881 0,754 0,639 0,545 0,470 0,410 0,360 0,320. 0,285 0,256 0,230 0.208 0,189 0,172 0,158 0.144 0,133 0,123 0.113 0,105 0,098 0,091 0,085 0,079 0,071 0,060 |
1,000 0,977 0,881 0,755 0,642 0,560 0,477 0,420 0,374 0,337 0,306 0.280 0,258 0,239 0,223 0,208 0,196 0,184 0,175 0,166 0,158 0,150 0,144 0,137 0,132 0,126 0,114 0,104 |
||
|
Примечание 1. В таблице 2 обозначено: b – ширина или диаметр фундамента, l - длина фундамента. 2. Для промежуточных значений n и l коэффициент α определяется путем | |||||||||||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.