Корреляционный и регрессионный анализ случайных величин. Коэффициент детерминизации и эмпирическое корреляционное отношение

5. Корреляционный и регрессионный анализ случайных величин

После того, как на основании теоретического анализа выявлено, что между изучаемыми объектами возможна связь, необходимо установить наличие связи. Установить наличие связи, а также получить представление о её характере можно с помощью сравнения параллельных рядов. Для этого единицы совокупности располагаются в возрастающем или убывающем порядке по факторному признаку. Параллельно записываются значения результативного признака. Путём сопоставления расположенных таким образом рядов значений выявляется существование связи и её направление.

Можно заметить, что с возрастанием признака x (длительность нагрузки) убывает признак y(нагрузка). Следовательно, между x и y имеется прямая зависимость, хотя и не полная, но выраженная достаточно ясно.

Для  упрощения расчётов составим таблицу 5.1.

Расчёт дисперсии групповых средних уровней нагрузки

Таблица 5.1

Группы по H(x)	Число значений нагрузки (n)	Нагрузка (T)	В среднем на группу (Tгр)	(Tгр – Tср)	(Tгр – Tср)2	(Tгр – Tср)2.n
0-6	6	52542,92875	8757,154791	4063,111	16508874,34	99053246,1
6-12	6	52278,19382	8713,032303	4018,989	16152271,97	96913631,8
12-18	6	50328,90594	8388,150991	3694,108	13646431,04	81878586,3
18-24	6	43791,10814	7298,518024	2604,475	6783288,17	40699729
24-30	6	30331,71504	5055,28584	361,242	130496,12	782976,691
30-36	6	14678,19422	2446,365704	-2247,68	5052054,93	30312329,6
36-42	6	4263,28919	710,5481978	-3983, 5	15868233,86	95209403,2
42-48	6	549,87525	91,64587579	-4602,4	21182062,78	127092377
48-54	5	20,08875	4,017750348	-4690,03	21996340,40	109981702
ИТОГО	53	248784,29911	4694,043379			681923981

Шаг интервала рассчитываем по формуле:

                                    R = 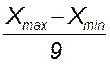,                              (5.1)

где X_max , X_min – максимальное и минимальное значения нагрузки соответственно.

Подставляем:

R = 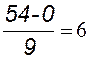 ч.

Определяем границы интервалов:

0+ 6= 6 ч,

6 + 6 =12 ч,

12 + 6= 18 ч,

18 + 6= 24 ч,

24 + 6 = 30 ч,

30 + 6 = 36 ч,

36 + 6 = 42 ч,

42 + 6 = 48 ч,

48 + 6 = 54 ч,

Среднее арифметическое вычислим по выражению:

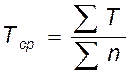                                     ,                                         (5.2)

где - суммарное значение нагрузки, МВт;

- общее число значений нагрузки.

Подставляем значения:

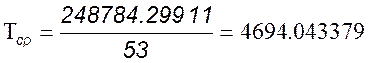 МВт.

Дисперсия групповых средних уровней нагрузки:

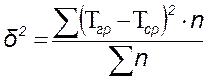                            .                                (5.3)

Вычисляем:

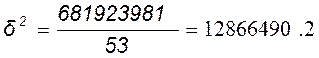 МВт.

Общую дисперсию нагрузки определим по формуле:

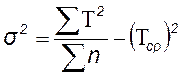                            .                               (5.4)

Подставляем значения:

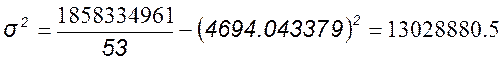 МВт.

Рассчитываем коэффициент детерминизации и эмпирическое корреляционное отношение по формулам:

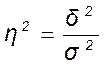                                  .                                            (5.5)

                                                                                  (5.6)

Делаем вычисления:

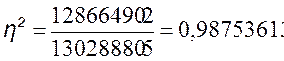
Коэффициент детерминизации показывает, что длительность нагрузки на 98.75% определяет вариацию нагрузки. Корреляционное отношение показывает, что связь между длительностью нагрузки и нагрузкой весьма тесная (=0,99375). Следовательно, имеет смысл провести регрессионный анализ.

Найдём теоретическое уравнение связи, имеющее линейный характер. Уравнение прямой в общем виде описывается так:

                         T(H) = a₀ + a₁.H .                                 (5.7)

Найти теоретическое уравнение связи – значит в данном случае определить параметры прямой. Эти параметры находятся методом наименьших квадратов, который даёт следующую систему нормальных уравнений для нахождения параметров прямой:

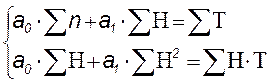                                                   (5.8)

Для решения этой системы уравнений данные берём из таблиц 5.1, 5.2. Следовательно, решение системы нормальных уравнений для нахождения параметров прямой следующее: