Практическая работа №3
Решение обратной задачи гравиразведки
Обратная задача гравиразведки заключается в вычислении по заданному распределению поля ускорения силы тяжести параметров анамалеобразующего тела, т. е. его размеров R, V, глубины залегания h.
Исходные данные:
Вариант №14
Таблица 1 – исходные данные
|
Δx, м |
δ, г/см3 |
δ, кг/м3 |
Аномалеобразующее тело |
|
20 |
0,7 |
700 |
Горизонтальный круговой цилиндр |
Решение обратной задачи гравиразведки для кругового горизонтального цилиндра
Из анализа решения прямой задачи кривая всюду положительна и симметрична относительно максимума, который находится над центром горизонтального цилиндра. Следовательно начало координат совпадает с максимумом кривой т.е.при x=0. Для точки, удаленной от максимума на расстояние x0,5 формула для вычисления глубины залегания центра шара будет иметь вид:
x0,5=h; (1)
где h - глубина залегания аномалеобразующего тела. Величины х0,5 и ∆gmax снимают с графика (рисунок 1).
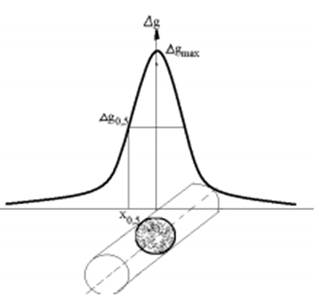
Рисунок 1 – Гравитационное поле над горизонтальным круговым цилиндром
Если известна избыточная плотность, то можно найти радиус цилиндра:
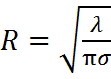 (2)
(2)
где, R – радиус цилиндра
(м); ![]() – линейная
плотность (избыточная масса) цилиндра (кг/см) и
– линейная
плотность (избыточная масса) цилиндра (кг/см) и ![]() –
избыточная плотность (г/см3).
–
избыточная плотность (г/см3).
Проведем качественную интерпретацию гравитационной аномалии полученной в ходе выполнения практической работы №2.
Исходя из того, что кривая аномалии силы тяжести везде положительна и симметрична относительно максимума, который будет находиться над центром горизонтального цилиндра, то начало координат совпадет с максимумом кривой, то есть х=0 (рисунок 2). Максимум кривой имеет значение Δgmax =0,938 мГал.
Для определения глубины залегания цилиндра возьмем на оси абсцисс точку удаленную от максимума на расстояние – х0,5, в которой значение аномалии равнялось бы Δg0,5 (рисунок 2).
Δg0,5=
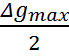 =
=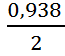 =0,469
мГал.
=0,469
мГал.
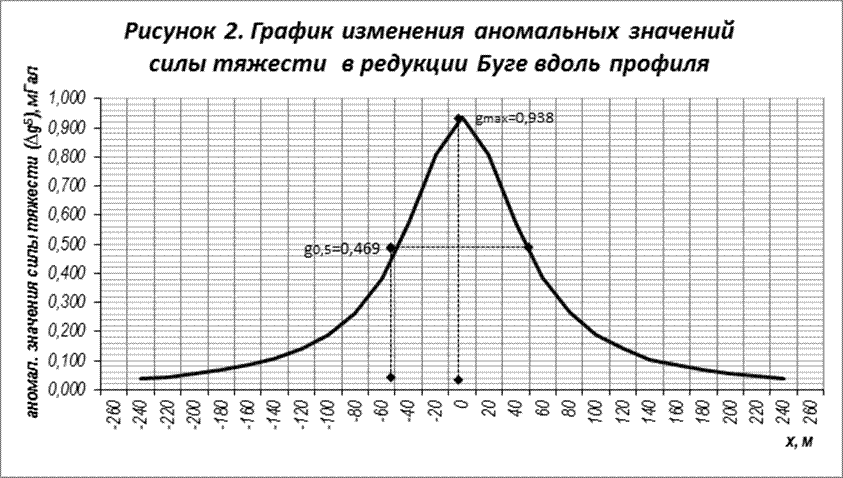
Опустив перпендикуляр из данной точки на кривой на ось абсцисс, определим значение x0,5, которое будет равняться x0,5=50 м (рисунок 2).
По формуле 1 определим глубину залегания горизонтального цилиндра.
Так как у нас имеется значение избыточной плотности, можно определить радиус цилиндра по формуле 2, но первоначально необходимо определить значение линейной плотности (избыточной массы) цилиндра (x0,5=h=50 м) по формуле:
![]() =
=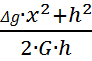 ;
;
Подставив известные значения получим:
![]() =
=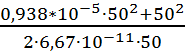 =3748161,1
(кг/см);
=3748161,1
(кг/см);
Теперь, подставив значение линейной плотности, определим радиус цилиндра R:
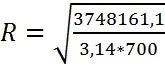 =41,3
(м).
=41,3
(м).
Все определенные параметры представлены в таблице 2.
Таблица 2 – определенные параметры для задания 1
|
Определенные параметры |
||||
|
Δgmax, мГал |
Δg0,5,мГал |
h, м |
λ, кг/см |
R, м |
|
0,938 |
0,469 |
50 |
3748161,1 |
41,3 |
Аналогично поступим и с заданием 2. Аномалия силы тяжести представлена на рисунке 3.
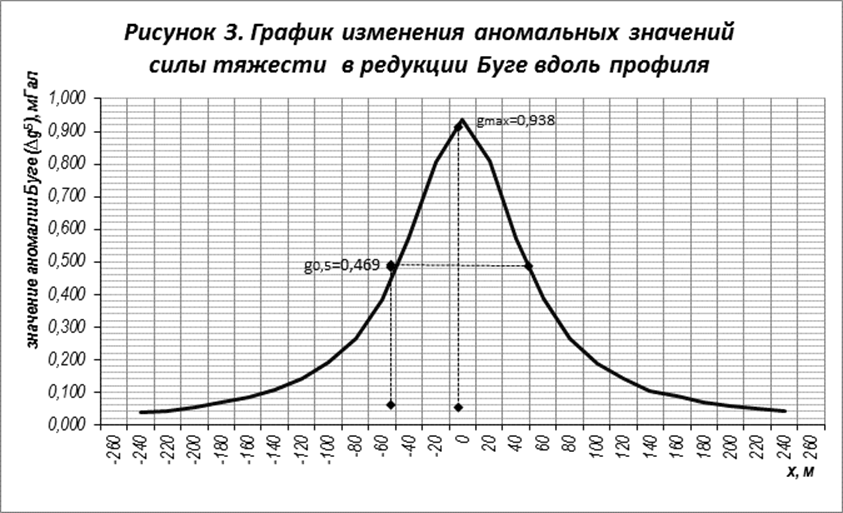
Максимальное значение аномалии наблюдается, так же как и в первом случае, на 0 пикете, и имеет значение Δgmax =0,938 мГал.
Для определения глубины залегания цилиндра возьмем на оси абсцисс точку удаленную от максимума на расстояние – х0,5, в которой значение аномалии равнялось бы Δg0,5 (рисунок 3).
Δg0,5=
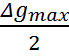 =
=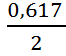 =0,309
мГал.
=0,309
мГал.
Глубина залегания аномалеобразующего тела - x0,5=h=55 м.
Определяем значение линейной плотности цилиндра по формуле:
![]() =
=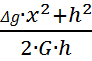 ;
;
![]() =
=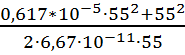 =2543400
(кг/см);
=2543400
(кг/см);
Теперь, подставив значение линейной плотности, определим радиус цилиндра R:
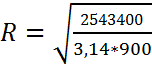 =30
(м).
=30
(м).
Всеопределенные параметры представлены в таблице 3.
Таблица 3 – определенные параметры для задания 2
|
Определенные параметры |
||||
|
Δgmax, мГал |
Δg0,5,мГал |
h, м |
λ, кг/см |
R, м |
|
0,617 |
0,309 |
55 |
2543400 |
30 |
Выводы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.