Современные пакеты программ ПЭВМ для анализа и синтеза электроприводов. Структурные преобразования и операции с передаточными функциями

                                            В. С. Захаренко

          СОВРЕМЕННЫЕ ПАКЕТЫ            ПРОГРАММ ПЭВМ ДЛЯ АНАЛИЗА

                 И СИНТЕЗА ЭЛЕКТРОПРИВОДОВ

Введение

В данном лабораторном практикуме излагаются приемы работы с программами MathCAD и Matlab Simulink при расчете систем управления электроприводами. Приводятся задания к лабораторным работам.

Изучение данного предмета предполагает успешное усвоение студентами дисциплин «Информатика», «Теория автоматического управления», «Основы математического моделирования», «Моделирование в электроприводах», «Системы управления электроприводами». Содержание лабораторных работ состоит в изучении приемов и работы с указанными программами и в изучении способов выполнения следующих расчетов:

–  структурные преобразования и операции с передаточными функциями;

–  построение логарифмических характеристик; – расчет переходных процессов.

Отчеты по лабораторным работам должны оформляться на отдельных листах формата A4 и должны содержать:

–  титульный лист;

–  цель работы;

–  задание;

–  вывод системы дифференциальных уравнений (при необходимости);

–  распечатку документа MathCAD или распечатки модели

Matlab и полученных в Matlab диаграмм или графиков;

–  выводы по проделанной работе и полученным результатам.

1.  Программа MathCAD

1.1.  Структурные преобразования и операции с передаточными функциями

Для структурных преобразований и работы с передаточными функциями необходимо пользоваться операцией Factor (Simplify для версий MathCAD ранее 14-й) символьных вычислений. Порядок работы рассмотрим на примере простейшей структурной схемы (рис. 1.1).

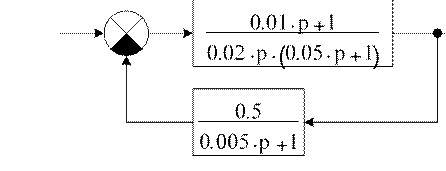
Рис. 1.1. Структурная схема для преобразования Передаточные функции прямого канала

                                      W_П( )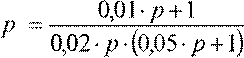 и обратной связи

                                          W_OC( )     .

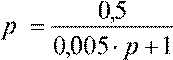Для получения передаточной функции данной структуры зададим в MathCAD функции аргумента p для передаточных функций прямого канала и обратной связи. Затем воспользуемся правилом структурных преобразований для получения общей передаточной функции и, используя операцию Factor, получим окончательный результат (рис. 1.2).

WП( )        WОС( ) (0.05⋅p + 1) 0.02⋅ ⋅p

WП( )p

W(p) :=

WП( )p ⋅WОС( )p + 1

10⋅(p + 200.0)⋅(p + 100.0) W(p) factor →

                                                                        3               2

                                                                      p   + 220.0⋅p   + 5000.0⋅p + 100000.0

Рис. 1.2. Фрагмент документа MathCAD с передаточными функциями

В знаменателе полученной результирующей передаточной функции присутствует полином 3-й степени. Если требуется разложить передаточную функцию на элементарные звенья, то следует воспользоваться функцией MathCAD polyroots. В качестве аргумента в данную функцию необходимо передавать матрицустолбец коэффициентов полинома. Элементы матрицы должны содержать коэффициенты при степенях аргумента, соответствующих номерам строк (рис. 1.3).

⎛⎛ ^100000.⎞⎞

                                                        ⎜⎜          ⎟^⎟             ⎛     −197.218       ⎞

                      p := polyroots ⎜⎜ ^5000. ⎟⎟         p = ⎜ −11.391− 19.424i⎟

⎜⎜ 220. ⎟⎟ ⎜ ⎟ ⎜⎜ ⎟⎟ ⎝ −11.391+ 19.424i⎠ ⎝⎝ 1 ⎠⎠

Рис. 1.3. Фрагмент документа MathCAD с определением корней

Для вещественного корня p постоянная времени соответствующего звена равна

1

                                                        T = − .

p

Комплексно-сопряженные корни соответствуют звену 2-го порядка. Установим связь между корнями и параметрами звена. Обозначим: α – вещественная часть, β – комплексная. Тогда корни

p₁ = α + jβ, p₂ = α − jβ.

(p − p₁) (⋅ p − p₂) (= p −α − jβ)⋅(p −α + jβ) = p² −2⋅α⋅ p +α² +β² =

                                    = (α2 +β2)⋅⎛⎜ 21 2 ⋅ p2 − 22 ⋅α 2 ⋅ p +1⎞⎟.

                                                 ⎝α +β           α +β          ⎠                  

Сравним теперь полученное выражение с характеристическим уравнением звена 2-го порядка T²⋅ p² + 2⋅T ⋅ξ⋅ p +1 и получим

                                                    T = ,

                                                       − 2⋅α     1        −α⋅ α² +β²              α

                              ξ = 2          2 ⋅       =        2         2         = −    .

                                                       α +β    2⋅T           α +β             p₁

Итак, определим параметры элементарных звеньев, вынеся за скобки коэффициенты при 0-й степени p (рис. 1.4).

K :=               K = 2

                     1                                            −3

T1 :=                         T1 = 5 × 10

200

1

T2 :=                          T2 = 0.01

100

                      1                                                  −3

T3 := −                       T3 = 5.071× 10

p

0

Re p

                      1                                                                                   ( ₁)

T4 :=T4 = 0.044                                                                                ξ4 := −ξ4 = 0.506

p

Рис. 1.4. Фрагмент документа MathCAD с расчетом параметров результирующей