Решение стратегических матричных игр. Основные теоретические сведения. Понятие игры, виды игр. Решение матричных игр в чистых стратегиях

Результатом вычислений этой функции является массив значений. Поэтому, прежде, чем задать эту функцию, нужно выделить диапазон ячеек, который всегда содержит 5 строк и k столбцов, где k – количество параметров регрессии, которые нужно определить. В нашем случае однофакторной регрессии нужно определить два параметра: a₁ и a₀, т. е. k = 2. Порядок ввода функции ЛИНЕЙН() следующий:

·  Выделить ячейки C5:D9 (5 строк и 2 столбца).

·  Вызвать мастер функций кнопкой  на панели инструментов. В категории Статистические выбрать функцию ЛИНЕЙН(). Задать аргументы этой функции, как показано на рис. 2.25. После ввода всех аргументов функции ЛИНЕЙН() следует нажать кнопку OK.

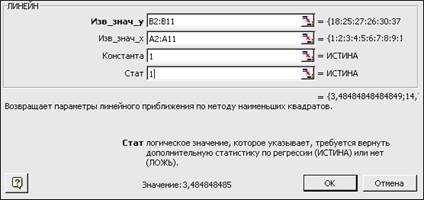
Рис. 2.25. Окно мастера функций для ввода функции ЛИНЕЙН()

·  Установить курсор в строку формул и нажать комбинацию клавиш Ctrl+Shift+Enter. После этого в строке формул появятся фигурные скобки, а весь предварительно выделенный диапазон заполнится значениями, которые выдает функция ЛИНЕЙН().

Аргументы этой функции Изв_знач_yи Изв_знач_x имеют тот же смысл, что и в функции НАКЛОН().

Аргумент Константа показывает, требуется ли, чтобы a₀ = 0. Если константа=ИСТИНА или опущена, то a₀ вычисляется обычным образом.

Аргумент Статистикапоказывает, требуется ли вывести дополнительную статистику по регрессии. Если статистика=ИСТИНА, то дополнительная информация выдается; если же статистика=ЛОЖЬ или опущена, то дополнительной информации нет. Ввод числа 1 равносилен вводу значения ИСТИНА.

Результаты расчетов параметров линейной регрессии показаны на рис. 2.23. Очевидно, что расчеты с помощью функций НАКЛОН() и ОТРЕЗОК() дают такие же результаты, что и функция ЛИНЕЙН(). Обратите внимание, что функция ЛИНЕЙН() дает параметры тренда в первой строке именно в следующем порядке:{a₁,a₀}. Остальные четыре строки выделенного нами диапазона заполняются различными статистическими характеристиками тренда (среднеквадратические отклонения полученных параметров тренда, расчетные величины для оценки достоверности полученных результатов и т. д.). Из этих величин в данной лабораторной работе нас будет интересовать только одна: коэффициент детерминации линейной модели R², который находится в третьей строке первом столбце: R² = 0,9373. Таким образом, линейный тренд достаточно точно описывает исходные данные.

3. Выполнение прогнозов по линейной модели. Прогнозы на три месяца вперед по линейной модели будем выполнять тремя способами:

·  с использованием рассчитанных нами параметров тренда;

·  с использованием функции ПРЕДСКАЗ();

·  с использованием функции ТЕНДЕНЦИЯ().

Введем в ячейки A12:D13 соответствующие заголовки, а в ячейки A14:A16 – номера месяцев, для которых нужно сделать прогноз (см. рис. 2.23).

1. В ячейку B14 введем формулу линейного тренда, в которой используются величины параметров, рассчитанные с помощью функции ЛИНЕЙН() в ячейках C5 и D5: =$C$5*A14+$D$5 и скопируем ее с помощью автозаполнения в ячейки B15 и B16.

2. В ячейку C14 введем формулу =ПРЕДСКАЗ(A14; $B$2:$B$11; $A$2:$A$11).

Для ввода формулы будем использовать мастер функций (рис. 2.26). Эта функция вычисляет прогноз для 11-го месяца (число 11 записано в ячейке А14). Аргументы Изв_знач_yи Изв_знач_x имеют тот же смысл, что и в функции НАКЛОН(). Мы задали эти значения абсолютными ссылками для того, чтобы затем правильно скопировать эту формулу.

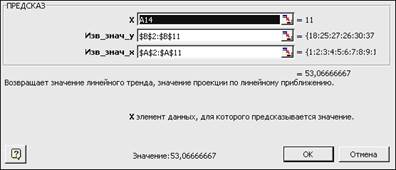
Рис. 2.26. Окно мастера функций для ввода функции ПРЕДСКАЗ()

Нажав кнопку OK для завершения ввода формулы в ячейку C14, скопируем эту формулу в ячейки C15 и C16 с помощью автозаполнения.

3. В ячейках D14:D16 нужно получить те же прогнозы с помощью функции ТЕНДЕНЦИЯ(). Эта функция своим результатом имеет массив значений, поэтому ее нужно вводить так же, как и функцию ЛИНЕЙН(): сначала выделить диапазон, в котором будет размещаться результат (D14:D16), затем вызвать мастер функций и задать аргументы функции ТЕНДЕНЦИЯ() как показано на рис. 2.27, а после нажатия кнопки OK установить курсор в строку формул и завершить ввод нажатием клавиш Ctrl+Shift+Enter.

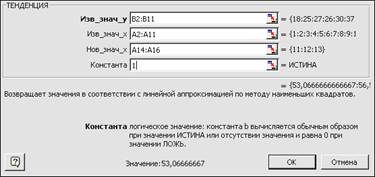
Рис. 2.27. Окно мастера функций для ввода функции ТЕНДЕНЦИЯ()

Аргументы Изв_знач_y,Изв_знач_x и Константаимеют тот же смысл, что и в функции ЛИНЕЙН(). Аргумент Нов_знач_x–это диапазон значений независимой переменной x (в нашем случае номера месяцев), для которого нужно получить прогнозные значения.

Результаты прогнозирования показаны на рис. 2.23. Естественно, что результаты, полученные различными способами, совпадают.

4. Расчет параметров экспоненциальной модели. Для определения параметров экспоненциальной модели  будем использовать встроенную функцию Excel ЛГРФПРИБЛ(). Эта функция  возвращает параметры экспоненциальной регрессии