Математическое описание динамических систем. Уравнение связи напряжения возбуждения и выходного напряжения генератора постоянного тока в режиме холостого хода

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ

Задача

Каково уравнение связи напряжения возбуждения и выходного напряжения генератора постоянного тока в режиме холостого хода?

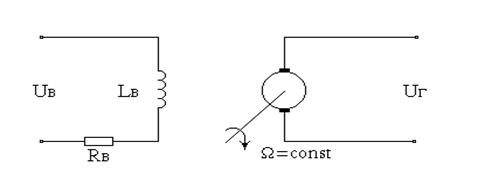
Задача

Записать в операторной форме уравнение связи входного и выходного напряжений LR-контура:

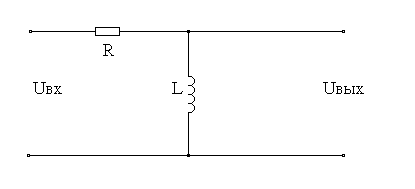
Варианты ответов:

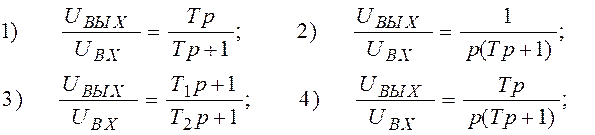
5) мало данных.

Задача

Решить предыдущую задачу для RC-контура:

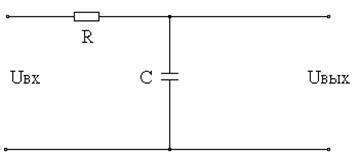
Варианты ответов:

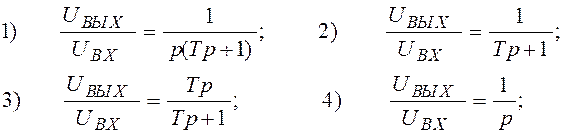
5) мало данных.

Задача

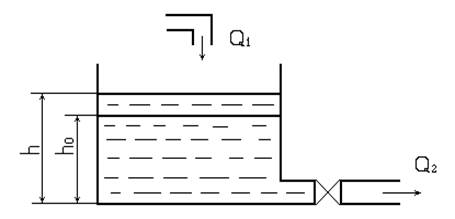
Составить дифференциальное уравнение регулируемого объекта - бака с протекающей через него жидкостью. Выходная величина рассматриваемой динамической системы - уровень жидкости .В качестве входной величины принимается расход жидкости на стоке . Бак имеет постоянную по высоте площадь поперечного сечения .

Задача

Составить дифференциальное уравнение пневматической системы, состоящей из камеры с объемом V и дросселя. Проводимость дросселя равна a. Входная и выходная величины - давление воздуха P₁  перед дросселем и давление P₂ за дросселем. Уравнение составить для малых отклонений переменных от состояния исходного равновесия.

Задача

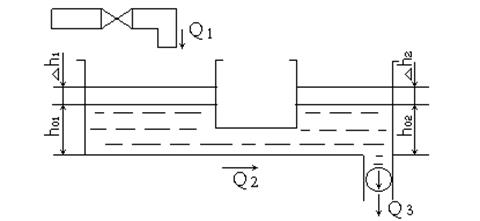
Составить дифференциальное уравнение системы, образованной двумя баками, приняв в качестве входной величины изменение расхода жидкости на притоке , а выходной - изменение уровня во втором по ходу жидкости баке. Площади поперечного сечения баков и . Допустить, что при малых отклонениях от исходного состояния равновесия расход между баками пропорционален разности уровней   и  и расход на стоке не зависит от уровня во втором баке.

Варианты  ответов:

1)   ;

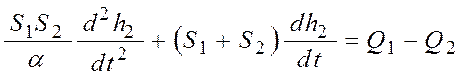2)   ;

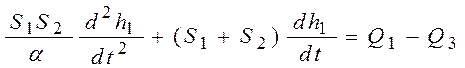3)   ;

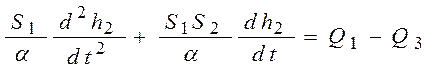4)   ;

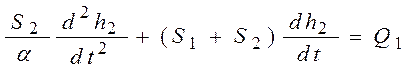5) мало данных.

Примечание:  - постоянный коэффициент.

Задача

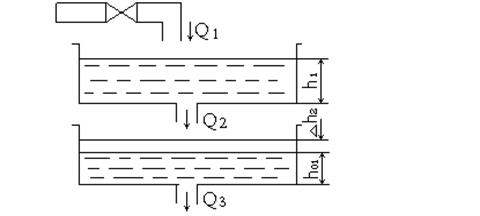
Составить дифференциальное уравнение (в линейном приближении) системы из двух баков, показанной на рисунке. В качестве входной переменной принять расход жидкости  на входе в систему; выходная переменная - изменение уровня  во втором баке. Площади баков одинаковы и равны .

Варианты ответов:

1)   ;

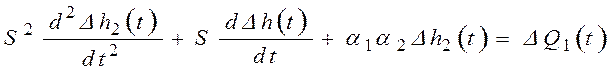2)   ;

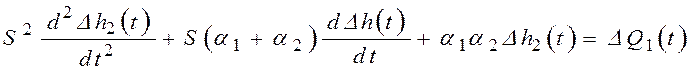3)    ;

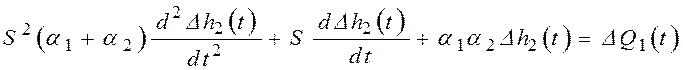4)   ;        

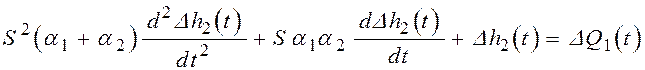5)   мало данных.

Примечание:  - коэффициенты расхода на стоке из баков в окрестности         исходного равновесного режима ; ; .

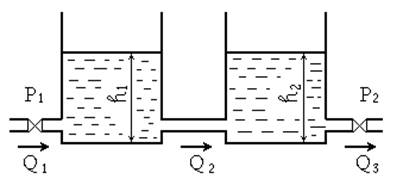
Задача

На рисунке изображена гидравлическая система, состоящая из двух баков, площади которых  и .  Составить дифференциальное уравнение, связывающее изменение уровня во втором баке  с изменением давления  на входе в систему. Допустить, что давление на входе не зависит от уровня в баке, а изменение расходов пропорционально перепадам давлений на постоянных гидравлических сопротивлениях.

Варианты ответов:

1)

;

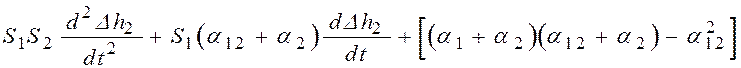
2)  

;

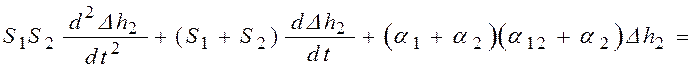
3)                

;

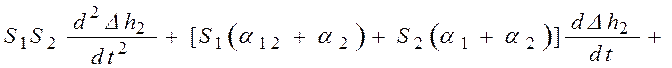
4) мало данных.

Примечание:  - постоянные коэффициенты.

Задача

Составить дифференциальное уравнение по условию предыдущей задачи, приняв в качестве входной величины изменение давления на выходе из системы. Влиянием уровня во втором баке на давление  в выходной магистрали пренебречь.

Варианты ответов:

1)

;

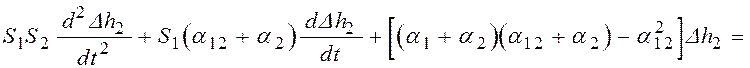
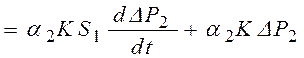2)

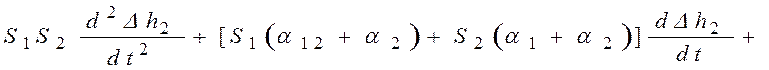
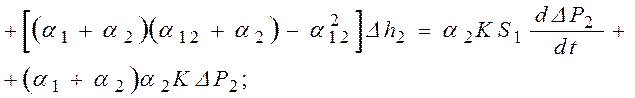
3)  

;

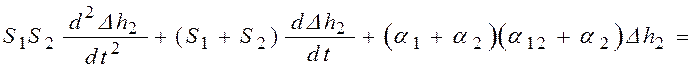
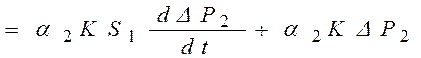4) мало данных.

Примечание:  - постоянные коэффициенты.

Задача

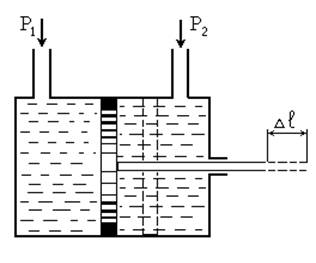
Составить дифференциальное уравнение гидравлического сервомотора, схематически изображенного на рисунке. В качестве входного воздействия рассматривается разность давлений . Выходная величина - изменение положения штока . При выводе уравнения инерцию движущейся массы не учитывать.

Варианты ответов:

1) ;

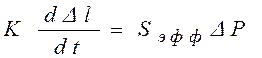2) ;

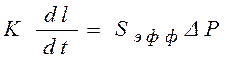3) ;

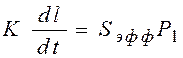4) мало данных.

Примечание: - коэффициент трения.

 - эффективная площадь поршня.

Задача

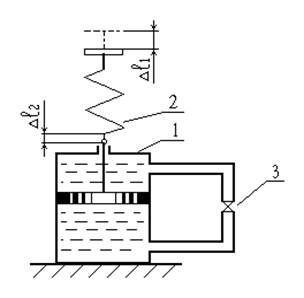
Составить дифференциальное уравнение системы, состоящей из гидравлического демпфера 1 и пружины 2 (см. рисунок). Входная величина - перемещение свободного конца пружины , выходная - перемещение штока . При составлении уравнения считать заданными коэффициент упругости пружины  и массу поршня . Коэффициент демпфирования определить зависимостью, пропорциональной вязкости жидкости и площади поршня  и обратно пропорциональной условному диаметру  проходного сечения вентиля 3.

Варианты ответов:

1)   ;

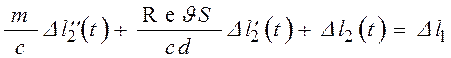2)   ;

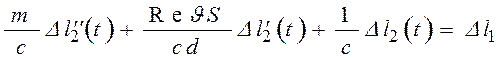3)   ;

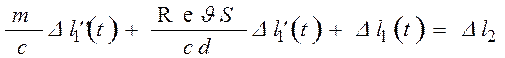4) мало данных.

Примечание:   - число Рейнольдса.

Задача

Составить дифференциальное уравнение малоинерционной термопары, считая, что передача тепла от среды к термочувствительному элементу осуществляется только теплопроводностью, термопара однородна, удельная теплоемкость материала термопары  , коэффициент теплопроводности , масса m и площадь воспринимающей тепло поверхности .

Варианты ответов:

1) ;

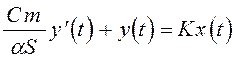2) ;

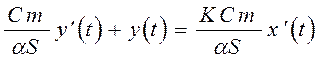3)   ;

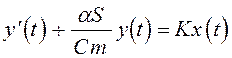4) мало данных.

Примечание:  - ЭДС и скорость изменения ЭДС термопары ;

 - температура измеряемой среды, ;

- передаточный коэффициент,   мВ/ .