Анализ присутствующих в схеме элементов. Составление функциональной схемы САР. Анализ устойчивости системы, страница 2

2. Анализ исходной замкнутой системы

Проведем исследование нашей исходной системы.

Составление передаточной функции

Составляем передаточную функцию системы от входа к выходу.

;

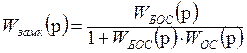где  - передаточная функция ветви без обратной связи.

    -  передаточная функция обратной связи.

 ;

;

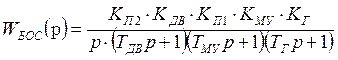Результирующая передаточная функция замкнутой системы

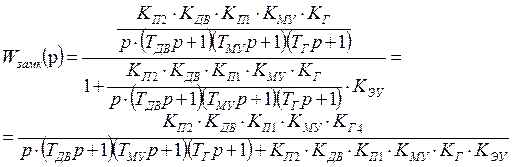
или в численном виде

.

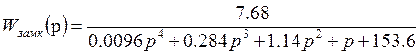Анализ устойчивости системы

Исследуем данную замкнутую систему на устойчивость по методу Гурвица. Для этого составим характеристическое уравнение:

;

По данному уравнению составляем матрицу коэффициентов:

;  

;

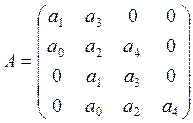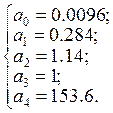
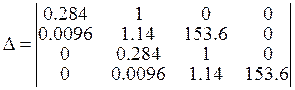Составляем и подсчитываем значения определителей Гурвица.

.

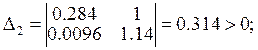
Анализируя полученные данные, делаем вывод: система неустойчива (так как имеются отрицательные определители).

Определим К_пред из условия положительности 3-го определителя:

Получим .

Для дальнейшего анализа системы возьмем

3. Анализ разомкнутой системы

Для дальнейшего исследования системы единичную обратную связь и проанализируем полученную разомкнутую систему.

Схема 5.

Составление передаточной функции

Составляем передаточную функцию разомкнутой системы от входа к выходу и общий коэффициент системы возьмем :

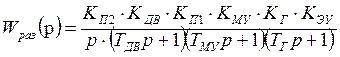
или в численном виде, где :

.

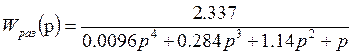Анализ устойчивости системы

а) Исследуем данную систему на устойчивость по методу Гурвица. Для этого составим характеристическое уравнение:

;

;

Поданному уравнению составляем матрицу коэффициентов:

;  

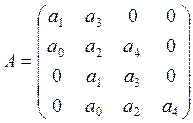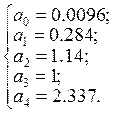
Составляем и подсчитываем значения определителей Гурвица.

.

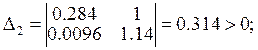
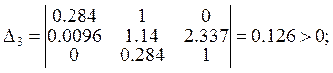
Анализируя полученные данные, делаем вывод: система устойчива (так как все определители положительны).

б) Исследуем данную систему на устойчивость по методу Михайлова. Для этого составим характеристический полином:

Подставляем значение :

или

Строим кривую Михайлова по характерным точкам

По виду построенной кривой делаем вывод: система устойчива, так как суммарный угол поворота равен  и кривая последовательно обходит все 4 квадранта комплексной плоскости, уходя в бесконечность в 4-м.

в) Исследуем данную систему на устойчивость по методу Найквиста. Для этого составим частотную передаточную функцию:

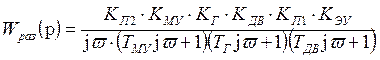
или ;

Запишем выражения для модуля и фазы частотной передаточной функции:

,

.

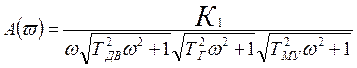Так как частотная передаточная функция достаточно проста, то можно найти U(w) и V(w), разлагая непосредственно комплекс W(jw) на вещественную и мнимую часть.

,

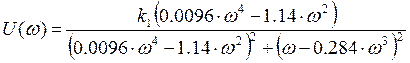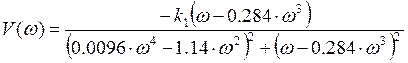, где K₁=2.337.

w	U(w)	V(w)
0	-2,664	-
+	0	0

По этим точкам строится АФХ системы.

По виду построенной кривой делаем вывод: система устойчива, так как кривая не охватывает точку (-1;j0).

4. Анализ системы по ошибке регулирования

Для проведения анализа системы по ошибке регулирования необходимо преобразовать исходную систему следующим образом.

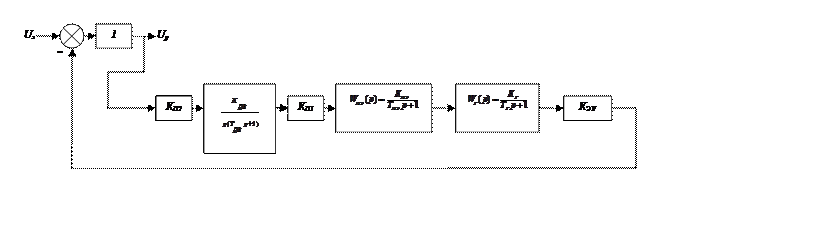
Схема 6.

Составление передаточной функции.

Составим передаточную функцию системы от входа к ошибке

 ;

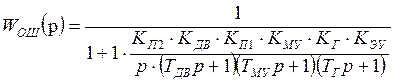Результирующая передаточная функция замкнутой системы

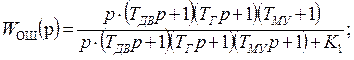
или в численном виде

.

Анализ устойчивости системы

Исследуем данную замкнутую систему на устойчивость по методу Гурвица. Для этого составим характеристическое уравнение:

;

Поданному уравнению составляем матрицу коэффициентов:

;  

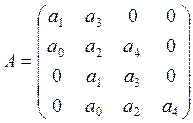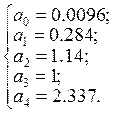
Составляем и подсчитываем значения определителей Гурвица.

.

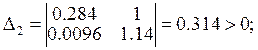
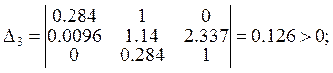
Анализируя полученные данные, делаем вывод: система устойчива (так как все определители положительны).

6. Библиографический список

1. «Теория автоматического управления» Методические указания по выполнению курсовой работы.

2. В.А. Бесекерский, Е.П. Попов «Теория автоматического регулирования» М.: -Наука, 1962. – 992 стр. ил.