Эконометрический анализ статистических данных, Оценка параметров моделей регрессии. Однофакторная регрессия

Лабораторная работа N  . Эконометрический анализ статистических данных. Оценка параметров моделей регрессии.

Компьютерная модель экономико-математического моделирования может выполнять функции анализа и подготовки прогнозов и планов. Модель объекта представляет собой математическое выражение, связывающее входные (независимые) переменные с выходными (зависимыми) переменными с помощью математических выражений, включающих некоторые параметры.

В данной лабораторной работе мы познакомимся с процессом эконометрического анализа на ряде простых примеров. Числовые параметры модели, как правило, определяются  в результате обработки статистических данных.

Однофакторная регрессия

В качестве первого примера рассмотрим прогнозирование объема продаж в зависимости от затрат на рекламную деятельность. Будем считать, что объем продаж зависит лишь от затрат на рекламу и пропорционален этим затратам (однофакторная линейная регрессия).

Введите представленные на Рис.1 в столбцах A, B данные.

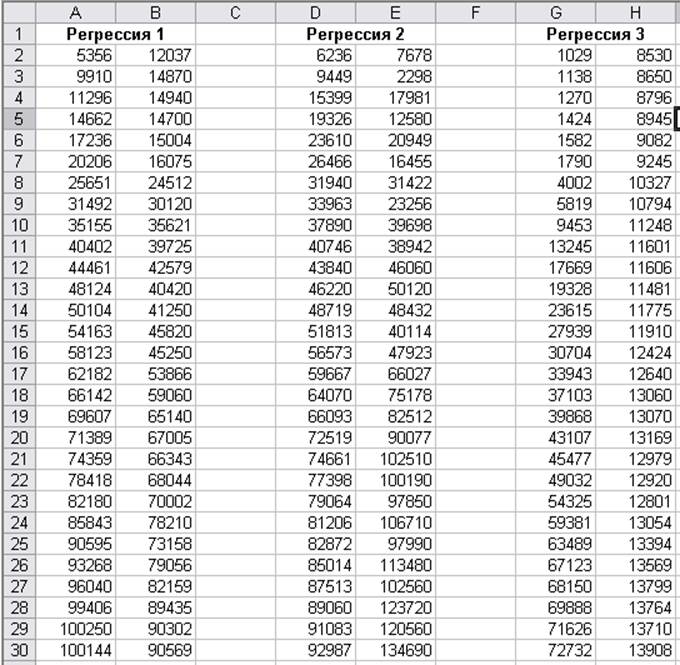
Рис. 1. Данные для однофакторной регрессии.

Постройте диаграмму (выберите тип точечная). Щелкните левой кнопкой мыши на любой статистической точке диаграммы, правой кнопкой вызовите контекстное меню и в появившемся окне диалога Линия тренда выберите тип Линейная. Выберите вкладку Параметры. Установите флажок показывать уравнение на диаграмме (Рис. 2), и, при желании, количественные показатели прогноза (вперед на … единиц).

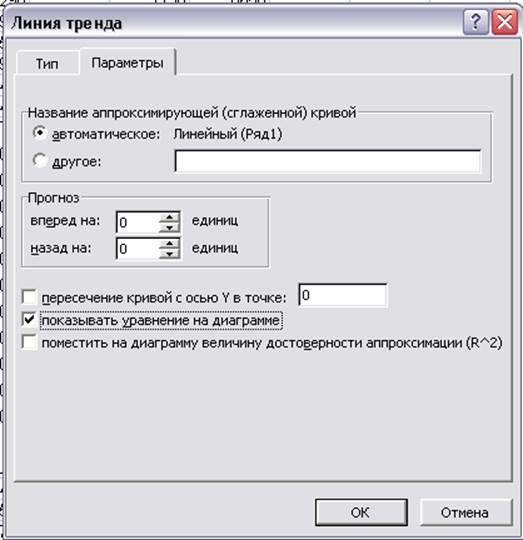
Рис. 2. Установка параметров линии тренда.

Самостоятельное задание

Аналогичным образом постройте диаграммы и определите уравнение однофакторной регрессии для данных, представленных в столбцах D, E и G, H на Рис.1. (Указание: используйте различные виды регрессионной зависимости, в частности, степенную и логарифмическую, и определите, какая зависимость лучше соответствует экспериментальным точкам в обоих случаях).

Многофакторная регрессия         

Как правило, поведение экономических функций определяется не одним, а несколькими параметрами. Сначала мы рассмотрим двухфакторную линейную модель на примере совместного влияния затрат на рекламу и цены на объем продаж товара.

Параметры линейной многофакторной модели оцениваются в Excel с помощью статистической функции ЛИНЕЙН (LINEST).

Будем рассматривать зависимость вида

Y(X1,X2) = a0 + a1*X1 + a2*X2,

Где X1, X2 – затраты на рекламу и цена товара соответственно, Y – объем продаж, a0, a1, a2 – параметры модели.

Введите данные в соответствии с Рис. 3.  

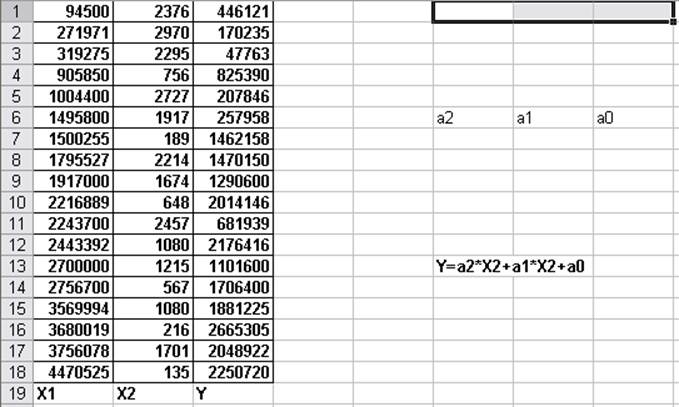
Рис. 3. Данные для оценки параметров функции двухфакторной линейной регрессии

Выделите ячейки F7:H7, вызовите мастер функций, выберите ЛИНЕЙН и в окне диалога заполните соответствующие окна в соответствии с Рис. 4..

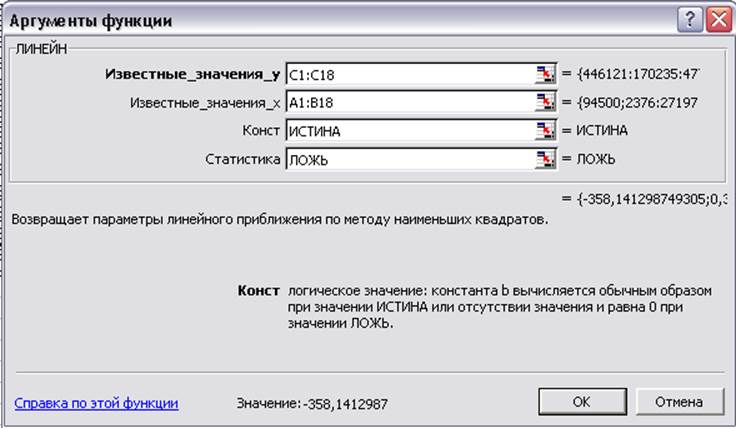
Рис. 4. Определение параметров функции ЛИНЕЙН

Запустите Мастер с помощью команды Ctrl+Shift+Enter. В результате Excel рассчитает параметры двухфакторной линейной регрессии и разместит их в выделенных вами ячейках (в указанном порядке).

Самостоятельное задание

Проведите аналогичным образом оценку параметров функции трехфакторной линейной регрессии (введите данные в соответствии с Рис. 5.).

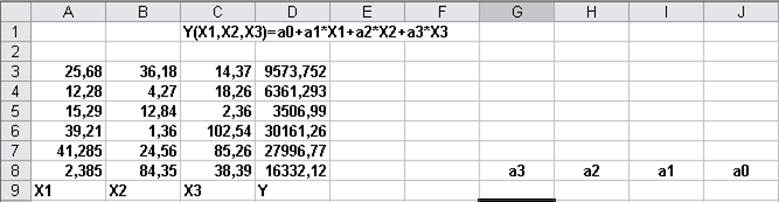
Рис. 5. Данные для трехфакторной линейной регрессии.

Оценка параметров производственной функции Кобба – Дугласа на основе статистических данных

До сих пор мы рассматривали случай линейной многофакторной регрессии. Сейчас мы покажем, как можно использовать подобный алгоритм для оценки параметров нелинейной многофакторной регрессии. В качестве примера рассмотрим зависимость производственной функции типа Кобба-Дугласа от затрат труда (L) и капитала (K). Функция Кобба-Дугласа имеет вид

.

Введите данные в соответствии с Рис. 6. Легко видеть, что путем логарифмирования данное выражение сводится к линейному виду. Заполните ячейки E5:G14 значениями ln(L), ln(K) и ln(Y). В ячейках J4:L4 разместите результат расчета при использовании функции ЛИНЕЙН. Определите значения параметров.

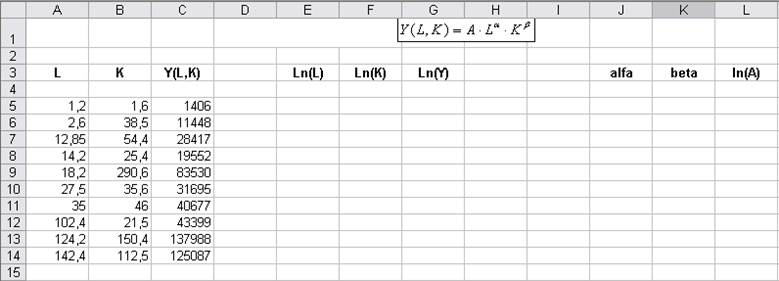
Рис. 6. Данные для трехфакторной нелинейной регрессии (функция Кобба-Дугласа).