Эффективное функционирование экономики предполагает наличие баланса между отраслями. Каждая отрасль при этом выступает и как производитель продукции и как потребитель продукции. Для отображения связей между производителями и потребителями используют таблицы межотраслевого баланса.
Алгебраическая теория анализа "затраты-выпуск" сводится к решению системы линейных уравнений, в которых параметрами являются коэффициенты затрат на производство продукции.
Рассмотрим структуру решения задачи построения межотраслевого баланса.
|
Этапы решения |
Содержание |
|
Объект моделирования |
Экономика, управляемая по параметрам равновесия переходных процессов и роста. Процесс выбора управляющего воздействия на отраслевом уровне. Моделируемые отрасли экономики: · отрасли-продавцы; · отрасли-покупатели; · распределение отраслей продавцов и покупателей по конечному и промежуточному спросу; · общий объем выпуска отраслей и экономики выпуска; · добавленная стоимость в отрасли. |
|
Проблемная ситуация |
Анализ качественного и количественного влияния отдельных отраслей друг на друга в целях выбора альтернатив управляющих воздействий. |
|
Ненаблюдаемые и неуправляемые параметры |
Величина объема выпуска продукции Xi в каждой отрасли |
|
Наблюдаемые параметры |
· статистические межотраслевые данные народнохозяйственной динамики за определенный период, содержание которые отражают связи между отраслями; · возможные технологические связи между отраслями; · коэффициенты прямых материальных затрат · коэффициенты полных затрат · плановый уровень конечной продукции Fi в каждой отрасли |
|
Параметры адекватности |
Параметры вектора объема выпуска продукции
|
|
Математический аппарат |
Система линейных уравнений в матричном виде n-го
порядка, (в данном случае 3-го порядка); матрица - матричный метод решения систем линейных уравнений |
|
Решение |
Выбор альтернатив при качественном анализе формирования планов отраслей и межотраслевых прогнозов. |
Весь производственный сектор разобьем на 3 отрасли (некоторые части хозяйства). Для расчета межотраслевого баланса нужно задать единицы измерения всех величин (тоны, финансовые показатели, штуки и т.д.). После этого все данные можно свести в таблицу межотраслевого баланса (табл. 2).
|
Производящие отрасли |
Потребляющие отрасли |
||||
|
I |
II |
III |
Конечная продукция |
Валовая продукция |
|
|
I |
|
|
|
|
|
|
II |
|
|
|
|
|
|
III |
|
|
|
|
|
|
Чистая продукция |
|
|
|
|
|
|
Валовая продукция |
|
|
|
|
|
Рассматривая таблица межотраслевого баланса по
столбцам, можно сделать вывод, что итог материальных затрат любой потребляющей
отрасли и ее условно чистой продукции равен валовой продукции этой отрасли.
Данный вывод можно записать в виде соотношения: 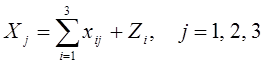 .
.
С другой стороны, рассматривая схему межотраслевого баланса по строкам для каждой отрасли, валовая продукция отрасли равна сумме материальных затрат потребляющих продукцию отраслей и конечные продукции данной отрасли:
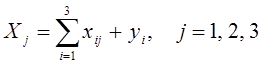 .
.
Балансовый характер таблица выражается в уравнениях:
![]() ;
;
![]() .
.
Основу экономико-математической модели
межотраслевого баланса составляет матрица коэффициентов прямых затрат ![]() , которая показывает, какое
количество продукции
, которая показывает, какое
количество продукции ![]() -той отрасли необходимо,
если учитывать только прямые затраты, для производства единицы продукции
-той отрасли необходимо,
если учитывать только прямые затраты, для производства единицы продукции ![]() -той отрасли.
-той отрасли.
Объем конечной продукции каждой отрасли можно
определить из следующего соотношения: ![]() .
.
Если заданы величины конечной продукции всех
отраслей, можно определить величины валовой продукции каждой отрасли из
соотношений: ![]() .
.
Обозначим матрицу ![]() ,
матица
,
матица ![]() называется матрицей полных затрат.
Коэффициенты матрицы полных затрат показывают, сколько всего нужно произвести
продукции
называется матрицей полных затрат.
Коэффициенты матрицы полных затрат показывают, сколько всего нужно произвести
продукции ![]() –той отрасли для выпуска единицы
продукции
–той отрасли для выпуска единицы
продукции ![]() -той отрасли.
-той отрасли.
Рассмотрим пример
расчета основных показателей межотраслевого баланса при условном делении
экономики на 3 отрасли. Предположим, что на плановый период заданы матрица
коэффициентов прямых затрат ![]() и вектор
конечной продукции
и вектор
конечной продукции ![]() (цифры условные):
(цифры условные):
|
|
|
Нужно определить:
1. Коэффициенты полных затрат.
2. Вектор валового выпуска.
3. Межотраслевые поставки продукции.
4.
Проверить продуктивность
матрицы ![]() .
.
5. Заполнить схему межотраслевого баланса.
Для решения задачи воспользуемся электронными таблицами Excel (Рис. 1)
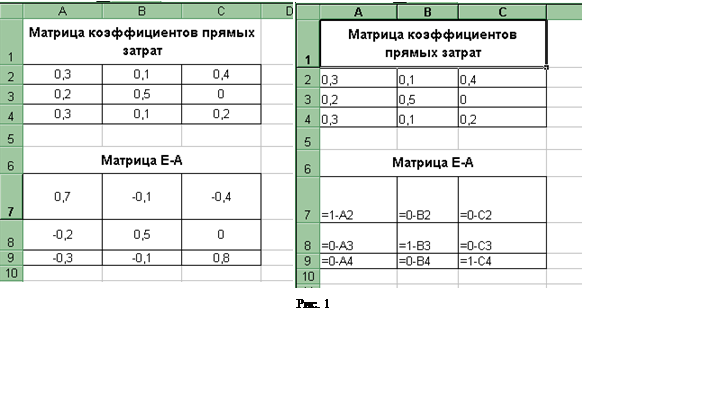 |
Для расчета коэффициентов матрицы ![]() , выделите диапазон ячеек E7 :G9; введите формулу для вычислений МОБР(А7 : С9), затем нажмите
клавиши CTRL+SHIFT+ENTER.
В силу неотрицательности
коэффициентов матрицы полных затрат, можно сделать вывод о продуктивности
матрицы
, выделите диапазон ячеек E7 :G9; введите формулу для вычислений МОБР(А7 : С9), затем нажмите
клавиши CTRL+SHIFT+ENTER.
В силу неотрицательности
коэффициентов матрицы полных затрат, можно сделать вывод о продуктивности
матрицы ![]() .
.
Элементы вектора конечного продукта ![]() вычислим по тому же принципу, используя
функцию МУМНОЖ(E7:G9;E2:E4) ( не забудьте переl вводом формулы выделить
диапазон G2 : G4, а после
нажмите клавиши CTRL+SHIFT+ENTER).
вычислим по тому же принципу, используя
функцию МУМНОЖ(E7:G9;E2:E4) ( не забудьте переl вводом формулы выделить
диапазон G2 : G4, а после
нажмите клавиши CTRL+SHIFT+ENTER).
Межотраслевые поставки вычисляются по формуле ![]() .
.
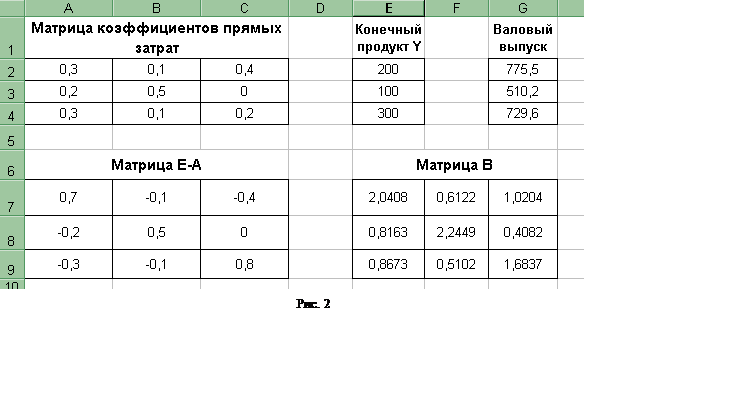
После выполненных вычислений заполните таблицу межотраслевого баланса (Рис. 3).
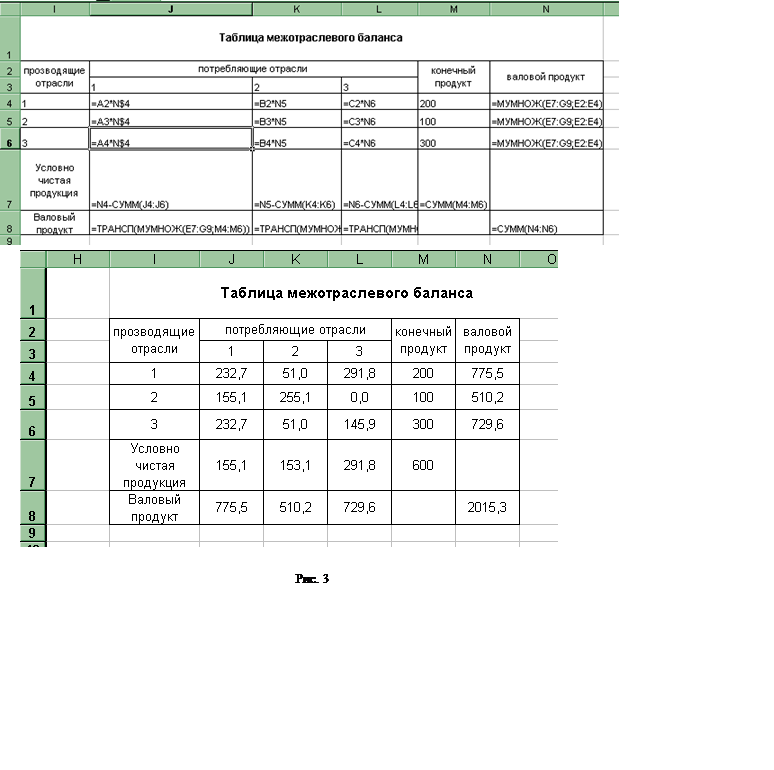
.
|
Вариант |
Исходные данные |
||
|
В-1 |
|
|
|
|
В-2 |
|
|
|
|
В-3 |
|
|
|
|
В-4 |
|
|
|
|
В-5 |
|
|
|
|
В-6 |
|
|
|
|
В-7 |
|
|
|
|
В-8 |
|
|
|
|
В-9 |
|
|
|
|
В-10 |
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.