Фирма должна отправить некоторое количество кроватей с трёх складов в пять магазинов. На складах имеется соответственно 15, 25 и 20 кроватей, а для пяти магазинов требуется соответственно 20, 12, 5, 8 и 15 кроватей. Стоимость перевозки одной кровати со склада в магазин приведены в таблице.

Как следует спланировать перевозку, чтобы её стоимость была минимальной?
Пусть Хij – количество кроватей, отправляемых со склада i в магазин j. Все Хij>=0, и в силу ограничений на возможности поставки со складов (предложение) и спрос в магазинах они удовлетворяют следующим условиям: (для предложения)
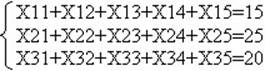
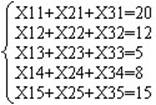
Стоимость перевозок равна
F=1*Х11+0*Х12+3*Х13+4*Х14+2*Х15+5*Х21+...+4*Х34+3*Х35
Так имеем следующую математическую модель
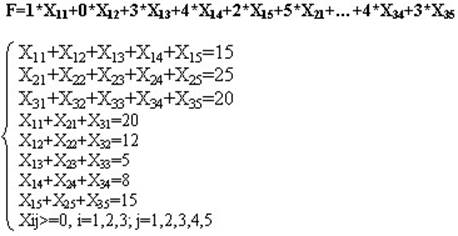
Такая задача есть задача линейного программирования, но специального вида. Её результат можно обобщить до транспортной задачи общего вида.
Однородный груз, имеющийся в m пунктах отправления (производства) А1, А2, ...Аm соответственно в количествах а1, а2, ...аm единиц, требуется доставить в каждый из n пунктов назначения (потребления) В1, В2, ..., Вn соответственно в количествах b1, b2 ..., bn единиц. Стоимость перевозки (тариф) единицы продукции из Аi в Вj известна для всех маршрутов AiBj и cij (i=1,m; j=1,n). Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится и запросы всех пунктов потребления удовлетворяются (закрытая модель), т. е.
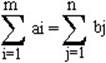
а суммарные транспортные расходы минимальны.

Будем называть любой план перевозок допустимым, если он удовлетворяет системам ограничений и требованием неотрицательности. Допустимый план будем называть
опорным, если в нем отличны от нуля не более m+n-1 базисных перевозок, а остальные перевозки равны 0. План будет называться оптимальным, если он, среди всех допустимых планов, приводит к максимальной суммарной стоимости перевозок.
Так как транспортная задача относится к задачам линейного программирования, её можно решать симплекс-методом; но в силу своих особенностей её можно решить гораздо проще.
Условия задачи удобно располагать в таблице, вписывая в ячейки количество перевозимого груза из Аi в Bj груза Xij>=0, а в маленькие клетки – соответствующие тарифы Cij.
Рис. 1.
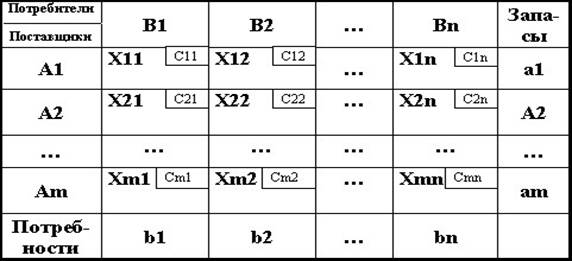
Затем решение задачи разбивается на два этапа:
1. Определение опорного плана
2. Нахождение оптимального решения, путем последовательных операций
Найдем вначале допустимое (опорное) решение транспортной задачи. Это решение можно находить, используя метод северо-западного угла или метод минимального
элемента.
Сущность состоит в том, что на каждом шаге заполняется левая верхняя клетка (северозападная) оставшейся части таблицы, причем максимально возможным числом: либо полностью вывозится груз из Аi, либо полностью удовлетворяется потребность Вj. Процедура продолжается, пока на каком-то шаге не исчерпаются запасы аi и не удовлетворятся все потребности bj. В заключение проверяют, удовлетворяют ли найденные компоненты плана Хij горизонтальным и вертикальным уравнениям.
Метод наименьшего элемента.
Сущность состоит в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действия аналогичны предыдущему методу.
Построим опорный план для рассмотренной выше задачи. Вначале построим его с помощью метода северно-западного угла.
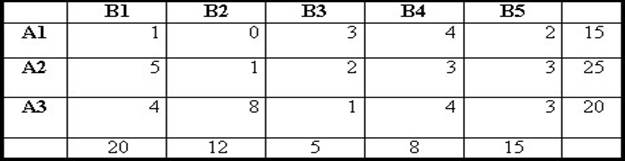
Магазин В1 подал заявку на 20 кроватей, но со склада А1 мы можем перевести 15 кроватей, ещё 5 кроватей мы перевезём со склада А2. Спрос для магазина В1 удовлетворён. Рассмотрим магазин В2. В него необходимо доставить 12 кроватей – доставим их со склада А2.
На складе А2 осталось 8 кроватей. Выделим из них пять для магазина В3. На складе А2 осталось 3 кровати. Выделим их на магазин В3. Но потребности магазина ещё не удовлетворены, поэтому выделим ему со склада А3 ещё пять кроватей. Осталось 15 кроватей – сколько требуется в магазин В5.

Построенный план допустимый, так как все заявки удовлетворены и все запасы израсходованы. Проверим, будет ли полученный план опорным: количество ячеек
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.