ТАБЛИЧНЫЙ МЕТОД ФОРМИРОВАНИЯ УРАВНЕНИЙ ЦЕПЕЙ
1.Цель работы:получить навык при составлении уравнений табличным методом.
2.Основные теоретические сведения
Табличный метод - наиболее общий метод составления уравнений цепи. В нем все уравнения, описывающие цепь, включены в общую систему уравнений,содержащую:
1) уравнения Кирхгофа для тока
2) уравнения Кирхгофа для напряжения
3) компонентные уравнения
Рассмотрим схему, содержащую b ветвей, n+1 узел и элементы R, G, L и C, а также источники тока и напряжения. Топология схемы описывается матрицей инциденций. Обобщенный закон Кирхгофа для токов и напряжений запишется в виде:
А · Iв = 0 (6.1)
UвТ - А · Un = 0 (6.2)
В самом общем случае уравнения, описывающие элементы цепи, можно представить в следующей форме:
|
К1 и К2 - безразмерные константы;
Wв1 и Wв2 - токи и напряжения независимых источников, учитывающие влияние начальных условий на конденсаторах и катушках индуктивности.
Для компактности будем использовать следующую форму записи:
Yв · Uв + Zв · Iв = Wв (6.3)
В табл. 6.1 представлены значения Yв, Zв и Wв для различных типов двухполюсных элементов.
Таблица 6.1.
|
Элемент |
Компонентное уравнение |
YВ |
ZВ |
WВ |
|
1.Резистор |
UВ - RВ * IВ = 0 |
1 |
- RВ |
0 |
|
2.Проводник |
GВ UB-IB = 0 |
GВ |
-1 |
0 |
|
3.Конденсатор |
pCB UВ - IВ = CB U0 |
pCB |
-1 |
CB U0 |
|
4.Катушка индуктивности |
UВ - pLВ IВ = -LВ I0 |
1 |
-pLB |
-LВ I0 |
|
5.Источник тока |
IB = JB |
0 |
1 |
JB |
|
6.Источник напряжения |
UB = EB |
1 |
0 |
EB |
В таблице U0 и I0 - начальные условия - напряжение на конденсаторе и ток через катушку.
Уравнения (6.1), (6.2) и (6.3) можно записать в следующей последовательности:
UвТ - А · Un = 0
Yв · Uв + Zв · Iв = Wв
А · Iв = 0
и представить в матричной форме:
|
(6.4)
или в общем виде: Т · X = W
В табличном методе нет никаких оснований различать источники и пассивные элементы - они вносятся в матрицу одинаково. Нумерация элементов может быть произвольной.
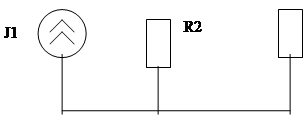
Запишем табличные уравнения для цепи, показанной на рис.6.1.
 |
|||||
|
![]()
![]()
![]()
![]()
![]()
 |
|
|||||
Рис.6.1 Простая цепь и ее направленный граф
В этом примере намеренно введены элементы R и G для того, чтобы наглядно показать разницу в описании каждого элемента.
Матрица инциденций для этой цепи имеет вид:
|
В результате табличные уравнения принимают вид:
|
|
Если в начальный момент времени на конденсаторе есть напря-жение U0 плюс которого приложен к узлу 1, а минус - к узлу 2, то седьмой элемент вектора в правой части равенства будет равен С3·U0.
Рассмотрим как вносится в граф 4х-полюсник.В графе каждая паразажимов 4х-полюсника представ-ляется двумя направленными отрезками (рис. 6.2). Соответственно, записываются два компонентных уравнения, приведенные в таб.2 в матричной форме для некоторых идеальных 4х-полюсников.
|
|
Рис.6.2.Четырехполюсник и его направленный граф.
Таблица 6.2. Компонентные уравнения идеальных 4х-полюсников.
|
4х-полюсник |
Условное обозначение |
Компонентные уравнения |
|
1.ИТУН |
|
|
|
2.ИНУН |
|
|
|
3.ИНУТ |
|
|
|
4.ИТУТ |
|
|
|
5.ОУ 6.Трансформатор |
|
« - » - для согластного
|
Запишем матрицу инциденций и компонентные уравнения в матричной форме для цепи, изображенной на рис.6.2.
|
Рис. 6.2. Активная цепь с ИНУН
Составим направленный граф для данной схемы (рис. 6.3).
|
Рис.6.3. Направленный граф активной цепи.
Ветвь 6 соответствует входным, а 7 - выходным зажимам УНИН. Матрица инциденций будет иметь вид:
1 2 3 4 5 6 7
|
1
А= 2
3
4
Запишем компонентные уравнения для каждой ветви графа в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.