









ЛАБОРАТОРНАЯ РАБОТА № 1
ДИСКРЕТНЫЙ ИСПЫТАТЕЛЬНЫЙ СИГНАЛ
1. Цель работы: Ознакомление с пакетом прикладных программ MathCAD и моделирование основных дискретных испытательных сигналов.
2. Краткие теоретические сведения.
Основное свойство дискретного сигнала: его значения определены не во все моменты времени, а лишь в счетном множестве точек. На практике отсчеты берут через равный промежуток времени, называемый шагом дискретизации. Шаг дискретизации должен удовлетворять теореме Котельникова.
В качестве испытательных сигналов, которые поступают на вход цифрового фильтра, в лабораторных работах используются три сигнала - дискретный аналог меандра и синусоиды, амплитуды которых равны 1, и случайный сигнал, выборки из которого можно получить с помощью программы-генератора случайных чисел пакета MathCAD.
При моделировании дискретной гармонической последовательности по аналоговому сигналу
![]()
удобнее брать отсчеты не через временной шаг дискретизации - Dt, а через фазовый угол - Df:
![]() .
.
Таким образом, если временной шаг дискретизации является константой для конкретного цифрового фильтра, то уменьшение угла – f эквивалентно уменьшению частоты аналогового сигнала s(t), из которого берутся отсчеты (и увеличению числа отсчетов за период). Такой подход дает возможность при анализе АЧХ цифровых фильтров не привязываться к тактовой частоте фильтра(шагу дискретизации) и вместо оси частот использовать ось f-фазового угла интервала дискретизации при текущем значении частоты. Одно и тоже значение угла f могут иметь фильтры с разным шагом дискретизации, но для разных частот w.
Генератор случайных чисел пакета MathCAD генерирует числа с равномерным распределением от 0 до некоторого заданного числа n. Для получения симметричного распределения относительно нуля нужно сместить все выборки случайного сигнала на n/2 вниз.
3. Порядок выполнения работы.
1. Познакомиться с пакетом прикладных программ MathCAD пользуясь системой помощи.
2. Пользуясь операторами и функциями системы MathCAD разработать алгоритм, моделирующий дискретный аналог меандра для 4-6 периодов. Число единичных ( и нулевых ) отсчетов взять от 5 до 8.
Построить график дискретного аналога меандра.
3. Используя тригонометрические функции разработать алгоритм, моделирующий дискретный аналог гармонического колебания для 3-4 периодов. Шаг дискретизации по фазе взять равным 10, 30, 45, 90 и 120 градусов. Для каждого шага дискретизации построить график.
4. Используя программу генерирования случайных чисел смоделировать отсчеты случайного процесса с равномерным распределением в диапазоне +-1.Число отсчетов взять равным от 50 до 100.
5. Смоделировать отсчеты аддитивной смеси двух гармонических сигналов и шума для отношения с/ш = от 1 до 5 по напряжению для 128 отсчетов. Гармонические дискретные сигналы заданы выражениями
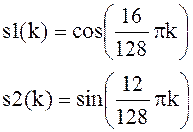
где k - номер отсчета
Построить графики сигнала, шума, смеси сигнала с шумом.
6. Распечатать графики дискретных аналогов меандра, дискретной гармонической последовательности для различных фазовых углов дискретизации, дискретной последовательности отсчетов сигнала, шума и смеси сигнал + шум.
4. Содержание отчета.
Отчет должен содержать распечатки программ моделирования испытательных сигналов и графики моделей дискретных сигналов, рассмотренных в пп.3.2 - 3.5.
5. Контрольные вопросы.
1.Какой сигнал называется меандром?
2.Какой сигнал называется детерминированным?
3.Какой сигнал называется случайным?
4.Какой сигнал называется дискретной гармонической последовательностью?
5.Почему удобнее задавать шаг дискретизации через фазовый угол?
6.О чем говорит теорема Котельникова?
7.В какую сторону нужно изменить фазовый угол дискретизации, чтобы увеличить или уменьшить частоту сигнала при неизменном временном шаге дискретизации?
ЛИТЕРАТУРА
1.Гоноровский И.С. Радиотехнические цепи и сигналы.
2.Конспект лекций по курсу "Теоретические основы информационной техники".
ЛАБОРАТОРНАЯ РАБОТА № 2
Быстрое преобразование Фурье (БПФ)
1. Цель работы: Научиться находить спектр сигнала с помощью БПФ и по известному спектру находить исходный сигнал с помощью обратного БПФ
2. Краткие теоретические сведения
Использование алгоритма дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств.
Выходом из положения явился алгоритм БПФ, где обработка входного массива сводится к нахождению дискретного преобразования Фурье массивов с меньшим числом членов. БПФ обладает всеми свойствами дискретного преобразования Фурье:
-БПФ есть линейное преобразование, то есть сумме сигналов отвечает сумма их БПФ
-Число различных коэффициентов C0,С1,C3,...CN, вычисляемых с помощью БПФ равно числу N отсчетов за период
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.