Выбор регулятора. Изучение особенностей дискретных регуляторов, аппроксимирующих аналоговые регуляторы и сравнение их с регуляторами, реализующими дискретные алгоритмы управления

2.  `Лабораторная работа 2

Выбор регулятора

          Цель работы: изучение особенностей дискретных регуляторов, аппроксимирующих аналоговые регуляторы и сравнение их с регуляторами, реализующими дискретные алгоритмы управления.

2.1.  Теоретические сведения

2.1.1.  Выделяют две основные группы систем управления: параметрически и структурно оптимизируемые. Системы, структура которых, т. е. вид и порядок описывающих их уравнений, задана, а свободные параметры подстраиваются под управляемый объект, называются параметрически оптимизируемыми. Системы управления называются структурно оптимизируемыми, если и структура, и параметры регулятора оптимально подстраиваются под структуру и параметры модели объекта.

Для параметрически оптимизируемых систем это различные типы ПИД-регуляторов невысокого порядка. Для структурно оптимизируемых систем это апериодические АР- регуляторы и регуляторы состояния.

2.1.2.  Обычно при проектировании используют правила настройки, критерии качества или задают расположение полюсов замкнутой системы. Задать поведение систем управления позволяют прямые методы расчета, которые основаны на использовании различных критериев качества. При проектировании систем управления, как правило, используют интегральные критерии качества — интеграл от ошибки управления, квадрата ошибки управления, абсолютной величины этой ошибки и т. д.

Применение  дискретных регуляторов, аппроксимирующих аналоговые регуляторы позволяет использовать накопленный опыт работы с аналоговыми регуляторами и применять уже хорошо известные правила настройки их параметров.

2.1.3.  Дискретный регулятор – это алгоритм управляющей ЭВМ реализующий требуемую зависимость между входным сигналом e(k) регулятора G_R и его выходным сигналом u(k).

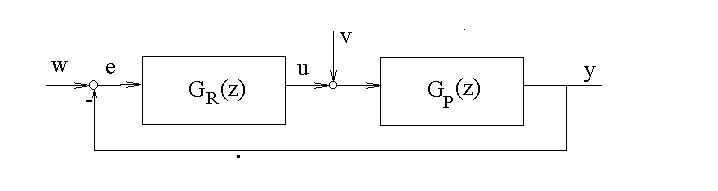
Рис.2.1. структурная схема замкнутой САР

2.1.4.  Уравнение непрерывного ПИД- регулятора включает три составляющие:  пропорциональную  П, интегральную  И  и  дифференциальную  Д.

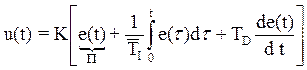
---    -----------     ------П        И               Д

где   K  -  коэффициент передачи;

T_I  -  постоянная интегрирования;

T_D -  постоянная дифференцирования.

2.1.5.  В дискретных системах непрерывный регулятор реализуется при малых тактах квантования T₀.  Дискретная передаточная функция ПИД- регулятора:

 

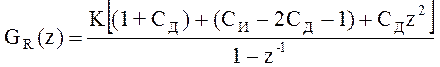
где     K  - коэффициент передачи регулятора;

Си  = T₀ / T_I  - коэффициент интегрирования  регулятора;

Сд = T_D/ T₀  - коэффициент  дифференцирования регулятора;

2.1.6.  В промышленных регуляторах реализуют следующие типовые законы регулирования

- пропорциональный  П;

- пропорционально - интегральный  ПИ;

- пропорционально - интегрально - дифференциальный  ПИД.

2.1.7.  Пропорциональный  П- регулятор  получают при  Си = 0 и  Сд = 0,  его передаточная функция:

G_R(z) = K;

где K  -  параметр  настройки  регулятора  (коэффициент передачи),

Особенность работы САР с П-регулятором в том, что выход u(k) регулятора пропорционален ошибке регулирования e(k) =w(k)-y(k) разности между  заданием и выходом объекта.  И чтобы выход П-регулятора был не нулевым, эта разность должна быть не нулевой,  т. е. должна быть статическая ошибка регулирования e(k) ≠0.

Следовательно, наличие статической ошибки регулирования является неотъемлемым  недостатком САР с П-регулятором

Статическая ошибка регулирования определяется коэффициентами усиления объекта  K_ОБ и регулятора K, 

e_СТ = K_ОБ/ (1+K_ОБK).

причем,  чем больше K, тем меньше статическая ошибка. Чтобы уменьшить статическую ошибку,  приходиться увеличивать коэффициент усиления регулятора,  что приводит к  неустойчивости САР.  .

2.1.8.  Пропорционально-интегральный  ПИ- регулятор получают при Сд = 0,  его передаточная функция

         

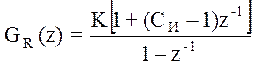
где  K и Си = T₀/TI  - параметры настройки регулятора.

Пропорционально- интегральный регулятор сочетает в себе достоинства П- и И-законов регулирования: пропорциональная составляющая обеспечивает достаточное быстродействие регулятора,  а  интегральная - ликвидирует статическую ошибку.

2.1.9.  Пропорционально- интегрально- дифференциальный ПИД- регулятор  имеет передаточную функцию:

 

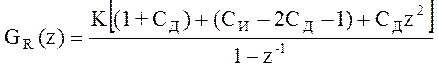
где  K,      Сд = T_D/T₀    и      Си = T₀/T_I  - параметры настройки регулятора.

 

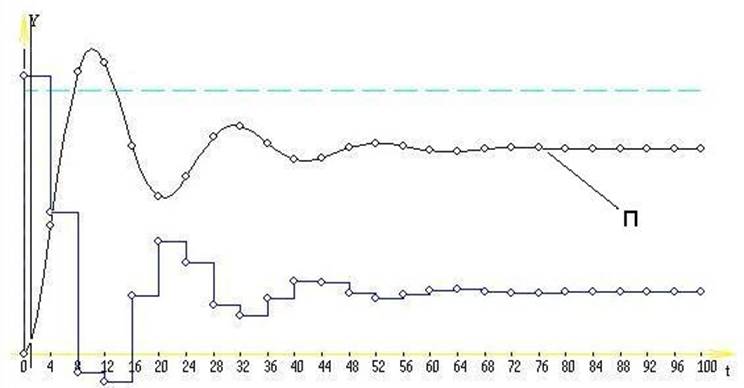
На Рис.2.2. приведены для сравнения процессы регулирования объекта различными регуляторами

2.1.10.  Дискретный апериодический регулятор АР синтезирует свою передаточную функцию, по параметрам дискретной передаточной функции объекта. Синтез выполняется так, что переходный процесс заканчивается через m интервалов,  где m – порядок передаточной функции объекта. Обычно m=2(3).

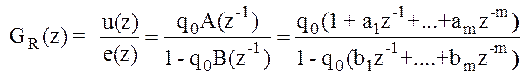
здесь а₁  . . . а_m, b₁. . .  b_m-   параметры передаточной функции объекта.

Из передаточной функции АР-регулятора следует, что его параметры  рассчитываются по известным параметрам объекта регулирования.

Таким образом, АР-регулятор не требует настроек своих параметров как ПИД-регулятор, но требует точных параметров объекта.

2.2.  Методические указания

2.2.1.  Изучите теоретические сведения, запишите определения и расчетные формулы законов регулирования.

2.2.2.  Запустите программу моделирования, выберите заданный объект регулирования и запишите его передаточную функцию Gp(s), постоянные времени и заданные ограничения.

Вариант объекта	0	1	2	3	4	5	6	7	8	9
№ объекта	5	1	5	2	4	3	1	2	3	4
Вариант парам	9	1	2	3	4	5	6	7	8	9
Постоянная Т1	22	15	10	20	12	16	18	24	20	15
Постоянная Т2	10	6	6	8	5	9	6	8	6	5
Пост. Т3 (числ.)	4	3	2	4	2	3	3	4	3	2
Коэф. затухания   e	0,2	0,4	0,2	0,3	0,5	0,4	0,3	0,5	0,3	0,4
Дин. ошибка  eдин<	0,3	0,2	0,4	0,3	0,2	0,4	0,3	0,2	0,4	0,3
Макс.упр. U(0)<	4	5	6	7	5	8	7	5	6	7