Исходные данные к расчёту пусковых и тормозных сопротивлений двигателей MTF, MTH
|
|
|
Последняя цифра шифра |
nн , об/мин |
I1 , А при 380 В |
cosϕн |
ηн , % |
I2н , А |
U2н , В |
Mmax , Н⋅м |
|||
|
0, 1, 2 |
3, 4 |
5, 6 |
7, 8, 9 |
|||||||||
|
P2н, кВт, при ПВ % |
||||||||||||
|
15 |
25 |
40 |
60 |
|||||||||
|
5 |
MTF011-6 |
2,0 – – – |
– 1,7 – – |
– – 1,4 – |
– – – 1,2 |
800 850 885 910 |
7,1 5,9 5,3 5,1 |
0,78 0,72 0,65 0,59 |
55,0 60,0 61,5 60,5 |
16,5 12,0 9,1 7,5 |
116 |
39 |
|
6 |
MTH111-6 |
3,5 – – – |
– 3,0 – – |
– – 2,5 – |
– – – 2,0 |
870 895 920 940 |
11,6 10,5 9,8 9,2 |
0,72 0,67 0,60 0,52 |
64,0 65,0 65,0 63,0 |
16,5 13,2 10,8 8,5 |
176 |
83 |
|
7 |
MTH112-6 |
5,3 – – – |
– 4,5 – – |
– – 3,6 – |
– – – 3,0 |
885 910 930 945 |
15,3 13,9 12,6 12,1 |
0,76 0,71 0,64 0,58 |
69,0 69,0 68,0 65,0 |
19,0 15,6 12,2 10,0 |
203 |
118 |
|
8 |
MTH211-6 |
8,2 – – – |
– 7,0 – – |
– – 5,6 – |
– – – 4,2 |
900 920 940 955 |
24,6 22,5 21,5 19,5 |
0,70 0,64 0,56 0,47 |
72,0 73,0 72,0 69,0 |
23,0 19,5 14,7 10,7 |
236 |
196 |
|
9 |
MTF(Н) 312-6 |
19,5 – – – |
– 17,5 – – |
– – 15,0 – |
– – – 12, 0 |
945 950 955 965 |
46,5 42,5 38,0 34,0 |
0,80 0,77 0,73 0,66 |
80,0 81,0 82,0 81,0 |
61,0 54,0 46,0 36,0 |
219 |
471 |
![]() Если
ДПТ ПВ работает с U=
const и Ф= const,
то пренебрегая реакцией якоря зависимости ω(Iя) (2.1) и ω(М)
(2.2) представляют собой прямые линии. При использовании скорости идеального холостого
хода ω0 =U
kФ в качестве базовой величины, номинальные значения Uн, Iн,
Mн, Фн и фиктивное номинальное сопротивление двигателя
Rн =Uн
Iн в относительных величинах запишутся:
Если
ДПТ ПВ работает с U=
const и Ф= const,
то пренебрегая реакцией якоря зависимости ω(Iя) (2.1) и ω(М)
(2.2) представляют собой прямые линии. При использовании скорости идеального холостого
хода ω0 =U
kФ в качестве базовой величины, номинальные значения Uн, Iн,
Mн, Фн и фиктивное номинальное сопротивление двигателя
Rн =Uн
Iн в относительных величинах запишутся:
ω I М
ν = ![]() ,
i =
,
i = ![]() ,
μ =
,
μ = ![]() ,
ω0 Iн Мн
,
ω0 Iн Мн
kФ R U φ = ![]() , ρ =
, ρ = ![]() , γ =
, γ = ![]() .
kФн Rн Uн
.
kФн Rн Uн
Электромеханическая и механическая характеристики в относительных единицах описываются уравнениями:
![]() γ
−ρ⋅i γ ρ
ν =
γ
−ρ⋅i γ ρ
ν = ![]() и ν = − 2
⋅μ. φ φ
и ν = − 2
⋅μ. φ φ
При номинальных значениях напряжения и магнитного потока (U =Uн, Ф = Фн) получим:
ν =1−ρ⋅i и ν =1−ρ⋅μ. (2.3)
![]() Rя
: Естественные характеристики с ρя =
Rя
: Естественные характеристики с ρя =
Rн
ν =1−ρя ⋅i и ν =1−ρя ⋅μ . (2.4)
На практике возможны несколько ситуаций при расчете пусковых сопротивлений. Рассмотрим их на примере с использованием рис. 2.1. Вначале строится естественная характеристика 1. Далее рассмотрим следующие ситуации:
1. Число ступеней задано и пуск нормальный.При этом задаются переключающими моментом μ2 или током i2 , которые должны быть на 10–20 % больше статических значений. Далее предположительно задаются максимальными значениями μ1(i1), чтобы для заданного количества ступеней получить одинаковые моменты переключения и пиковые для всех характеристик. Практически эти построения проводятся методом подбора легкими линиями на миллиметровой бумаге.
2. Число ступеней задано и пуск форсированный. В данном случае задаются максимально допустимыми значениями μ1 или i1 и подбирают момент μ2 или ток i2 переключения.
3. Число ступеней неизвестно, а задано ускорение. Если задано ускорение исполнительного органа механизма, то его вначале приводят к скорости якоря, получая угловое ускорение ε. По уравнению движения электропривода определяют средний пусковой момент Мп = Мс + J ⋅ε и его относительное значение μoп. Далее, задаваясь одинаковыми отклонениями (μ1 −μп) = (μп −μ2), подбирают характеристики и определяют количество пусковых ступеней. Окончательное их число уточняется после расчета пусковой диаграммы с учетом времени срабатывания аппаратуры.

После построения пусковых характеристик определяют сопротивления
ступеней по длине отрезков при номинальном моменте или токе (рис. 2.1, б)
ρп1 = de![]() af
, ρп2
= cd
af
, ρп2
= cd![]() af
, ρп3
= bc
af
, ρп3
= bc![]() af
, а затем в абсолютных величинах Rп1 = ρп1 ⋅ Rн ,
Rп2 = ρп2 ⋅Rн, Rп3
= ρп3 ⋅Rн (рис.
2.1, а).
af
, а затем в абсолютных величинах Rп1 = ρп1 ⋅ Rн ,
Rп2 = ρп2 ⋅Rн, Rп3
= ρп3 ⋅Rн (рис.
2.1, а).
1.
 Число
ступеней задано и пуск нормальный. В этом случае, как и при графическом, задаются
моментом μ2
или током i2 переключения. Соотношения между максимальным значением
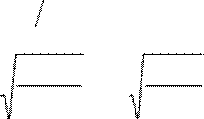
и значением переключения λ =
μ1
Число
ступеней задано и пуск нормальный. В этом случае, как и при графическом, задаются
моментом μ2
или током i2 переключения. Соотношения между максимальным значением
и значением переключения λ =
μ1![]() μ2
= i1
i2 определяются как:
μ2
= i1
i2 определяются как:
1 1
λ = m+1 = m+1 ,
ρя ⋅μ2 ρя ⋅i2
где m – число ступеней пускового сопротивления.
2. Число ступеней задано и пуск форсированный. В этой ситуации опять же задаются максимально допустимыми значениями μ1 или i1. Соотношения значений:
λ = m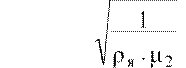 .
.
3. Число ступеней не задано. В данном случае задаются μ1 и μ2 в соответствии с режимами, а число ступеней определяется по выражению
m 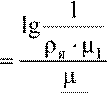 .
.
lg
Если число m получается дробным, то изменяют μ1 или μ2 так, чтобы получить m целым числом. По принятым значениям рассчитывают λ. После определения соотношения λ находят полные значения сопротивлений: R3 = Rя ⋅λ; R2 = R3 ⋅λ; R1 = R2 ⋅λ или
Rп3 = Rя ⋅(λ −1); Rп2 = Rп3 ⋅λ; Rп1 = Rп2 ⋅λ.
Аналитический метод более простой и точный, но если по каким-то условиям на разных пусковых ступенях требуются разные значения максимальных или переключающих величин, то он не применим.
2.1.2. Расчет пусковых сопротивлений для ДПТ последовательного возбуждения при помощи
Данный способ основан на том, что если для семейства характеристик (рис. 2.2, б) провести прямые линии через две точки при одинаковых значениях токов I1 и I2 , то они пересекутся в одной точке «0».
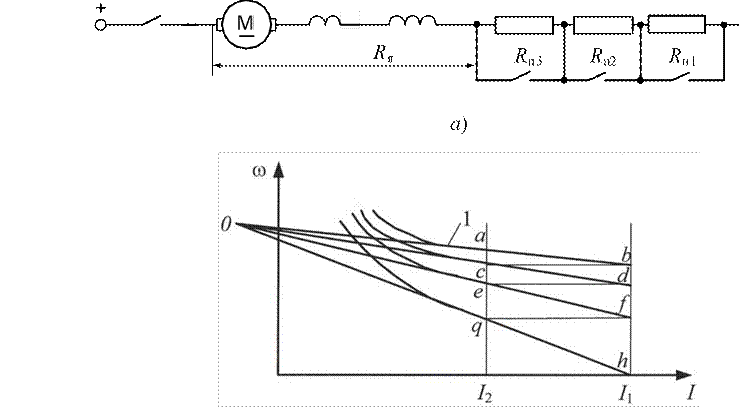
б)
Рис. 2.2. Схема включения ДПТ последовательного возбуждения (а) и построение лучевой диаграммы (б)
Порядок построения следующий:
1. Строится естественная характеристика 1 (рис. 2.2, б).
2. Исходя из желательных значений максимального момента определяется ток I1 и рассчитывается полное сопротивление силовой цепи при неподвижном якоре R =U / I1.
3. Для получения одинаковых значений максимальных и переключающих токов при заданном количестве ступеней предположительно задаются током I2 и скоростью двигателя ωи.q в точке «q» при полностью введенном сопротивлении (аналитически):
![]() U
− I2 ⋅ R ,
U
− I2 ⋅ R ,
ωи.q = ωе.a ⋅
U − I2 ⋅ Rя
где ωe.a – скорость на естественной характеристике в точке «a» при токе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.