Постановка задачи и допущения. Нормальный режим. Анализ протекания переходного процесса. Векторная диаграмма для начального момента трехфазного КЗ простейшей цепи
Лекции по курсу «ПЕРЕХОДНЫЕ ПРОЦЕССЫ В СИСТЕМАХ ЭЛЕКТРОСНАБЖЕНИЯ»
Лекция 4. Переходный электромагнитный процесс при трехфазном КЗ в простейших цепях
доктор технических наук,
профессор
Токочакова Надежда Владимировна
Постановка задачи и допущения. Нормальный режим
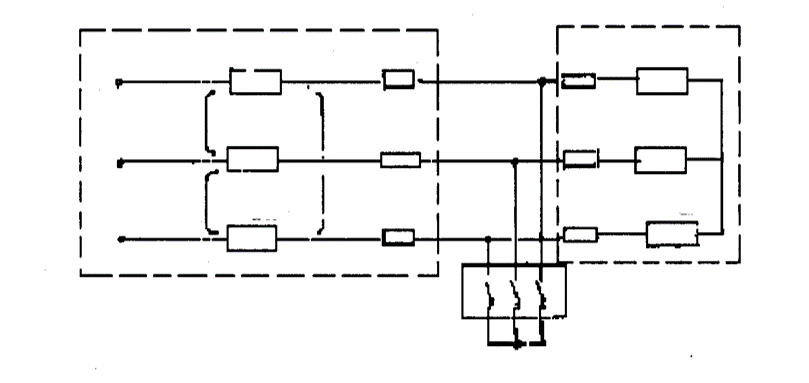
Трехфазную симметричную цепь с сосредоточенными активными и индуктивными сопротивлениями при отсутствии в ней трансформаторных связей называют простейшей трехфазной цепью.
Электромагнитный процесс в такой цепи рассмотрим при допущении, что ее питание осуществляется от источника бесконечной мощности. Такой источник характеризуется неизменностью напряжения на шинах по амплитуде и по частоте:
Un – действующее значение напряжения источника питания;
α – фаза включения, (т. е. угол между вектором напряжения фазы А и действительной осью
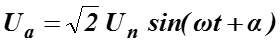
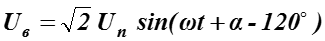
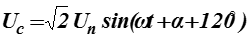
UA
ic
ia
IA
Ta
α
i0в
iв
В качестве основного допущения считаем, что между токами и напряжениями рассматриваемых цепей сохраняется линейная зависимость и, следовательно, они могут быть связаны линейными дифференциальными уравнениями с постоянными коэффициентами.
В рассматриваемой схеме емкость не учитывается, что исключает возможность возникновения колебательных контуров, а это значительно упрощает анализ протекания переходного процесса в цепи.
В нормальном режиме работы цепи по фазам протекает ток, определяемый напряжением источника питания и результирующим сопротивлением:
Где – действующее значение периодической составляющей;
– полное сопротивление цепи;
– активное сопротивление цепи;
– индуктивное сопротивление цепи;
– угол сдвига между напряжением и током той же цепи.
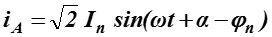
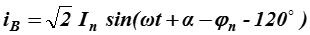
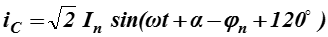
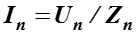
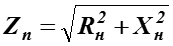
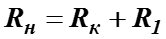
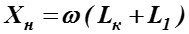
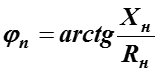
Анализ протекания переходного процесса
При КЗ в точке К простейшая электрическая цепь распадается на две независимые цепи (обозначим их М и N), одна из которых – М – остается присоединенной к источнику, а другая – N – превращается в короткозамкнутый контур, ток в котором будет поддерживаться до тех пор, пока запасенная в нем энергия не перейдет в тепло в резисторах R1.
Для части схемы N уравнение баланса напряжений будет:
Решением уравнения будет:
где i0 – начальное значение свободного тока,
– постоянная времени затухания свободного тока.
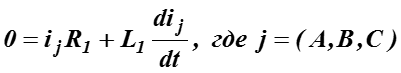
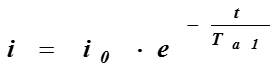
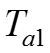
Уравнение показывает, что на участке N имеется лишь свободный ток, который затухает по экспоненциальному закону с постоянной времени Ta:
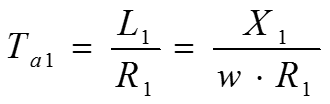
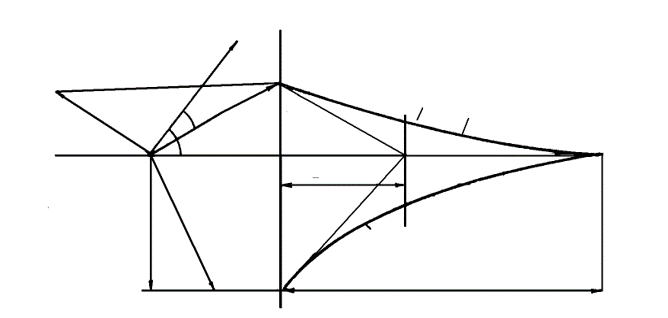
Проекции вращающихся векторов токов Ia, Ib, Ic на неподвижную ось t-t дают начальные мгновенные значения токов iОА, iОВ, iОС, которые затухают с одинаковыми постоянными времени .
Касательная к любой точке экспоненты в принятом для оси времени t масштабе дает значение постоянной времени . Это свойство используется для опытного определения постоянных времени затухания апериодических свободных токов. Для большей точности точку, к которой проводят касательную, нужно брать в начальной (более крутой) части кривой. За время апериодический ток уменьшается в e = 2,71 раз или до 1/e = 0,368 своего начального значения. В соответствии с этим, величине можно дать такое определение: это время, в течение которого переменная величина уменьшается до 0,368 своего начального значения.
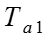
После затухания апериодической составляющей заканчивается переходный процесс в части цепи N за t = 0,1...0,3 с.
В одной из фаз свободный ток может отсутствовать, если в момент возникновения КЗ предшествующий ток в этой фазе проходил через нуль, при этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по направлению. Поэтому в начальный момент трёхфазное КЗ является несимметричным КЗ, так как начальные значения свободного тока каждой фазы различны.
Рассмотрим протекание переходного процесса на участке М, получающем питание от источника бесконечной мощности.
Так как суммарное сопротивление цепи, к которой присоединен источник, уменьшилось, то ток в общем случае должен увеличиться и должен измениться и угол сдвига тока относительно напряжения.
Любую синусоидальную величину можно представить в виде неизменного по величине вектора, вращающегося относительно неподвижной оси t-t с частотой вращения ωc. Проекции этого вектора на неподвижную ось t-t дают мгновенное
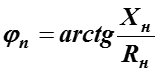
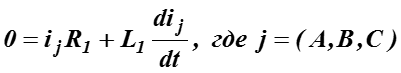
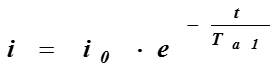
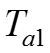
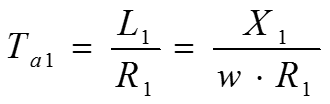
