1.68) Матрица рассеяния многополюсника.Смысл элементов матрицы рассеяния.
2.69) Матрицы сопротивлений и проводимостей.
![]() В СВЧ диапазоне линия передачи и её
отдельные элементы могут быть представлены в виде многополюсника, характеризующегося
матрицей рассеяния
В СВЧ диапазоне линия передачи и её
отдельные элементы могут быть представлены в виде многополюсника, характеризующегося
матрицей рассеяния ![]() таким
образом, что
таким
образом, что ![]() , где
, где ![]() - вектор столбец выходных напряжений,
- вектор столбец выходных напряжений, ![]() - вектор столбец входных напряжений.
- вектор столбец входных напряжений.
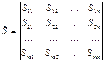
![]()
![]()
![]()
![]() - квадратная матрица nxm, в которой
элемент
- квадратная матрица nxm, в которой
элемент ![]() - коэффициент
передачи из i-го канала в j-й.
- коэффициент
передачи из i-го канала в j-й.
Диагональные элементы матрицы являются коэффициентами отражения каналов, а недиагональные – коэффициентами передачи.
Многополюсники,
для которых выполнятся условие ![]() , наз. взаимными.
Матрица рассеяния взаимного многополюсника симметрична (
, наз. взаимными.
Матрица рассеяния взаимного многополюсника симметрична (![]() ).
).
В общем случае элементы матрицы представляют собой комплексные величины.
Наряду
с уравнением (1) можно записать выражение связывающие столбцы напряжений и
токов: ![]() ;
; ![]() , где Z – матрица сопротивлений; Y –
матрица проводимостей.
, где Z – матрица сопротивлений; Y –
матрица проводимостей.
Вывод матрицы сопротивлений:
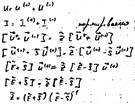
![]() - матрица сопротивлений.
- матрица сопротивлений.
Матрица проводимостей находится аналогично.
![]() - матрица проводимостей
- матрица проводимостей
Матрицы
сопротивлений и проводимостей связаны с матрицей рассеяния: ![]() ,Е – единичная матрица. Для описания
4-хполюсника применяют матрицу передачи
,Е – единичная матрица. Для описания
4-хполюсника применяют матрицу передачи ![]() , связывающую напряжение на входе и на
выходе 4-хполюсника:
, связывающую напряжение на входе и на
выходе 4-хполюсника: ![]() .
.
3.70) Матрица симметрии. Определение вида матрицы рассеяния.
Симметричные многополюсники инвариантны относительно перестановки плеч:
![]()
![]() – квадратная матрица симметрии с
ненулевыми элементами, равными ±1, разноположительными на пересечении I-ой строки и j-го столбца, если при
перенумеровании I-e плечо меняется на j-е.
– квадратная матрица симметрии с
ненулевыми элементами, равными ±1, разноположительными на пересечении I-ой строки и j-го столбца, если при
перенумеровании I-e плечо меняется на j-е.![]()
их
может быть много ![]()
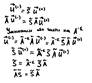 |
Собственные числа – это коэффициенты отражения во всех плечах многополюсника, при подаче на него набора падающих волн, соответствующего собственным векторам.
Пусть произведена перенумерация плеч, тогда:
Определение вида матрицы рассеяния:
1.
Определяем вид матрицы симметрии ![]()
2.
Определяем собственные числа ![]() и собственные
векторы
и собственные
векторы ![]() матрицы симметрии
матрицы симметрии ![]()
3.
Используя входные напряжения в соответствии с собственными векторами матрицы
симметрии, определяют коэффициенты отражения во всех плечах многополюсника
(т.е. собственные числа); составляют ![]() матрицу,
диагональные элементы которой являются коэффициенты отражения.
матрицу,
диагональные элементы которой являются коэффициенты отражения.
4.
Составляется модальная матрица ![]() , столбцами которой
являются собственные векторы матрицы симметрии.
, столбцами которой
являются собственные векторы матрицы симметрии.
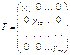
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.