













В современном машиностроении применяются два способа получения программных движений рабочих органов машины, необходимых для выполнения рабочего процесса. Первый способ, широко используемый в цикловых однодвигательных машинах, состоит в том, что на вход двигателя подается входной сигнал, обеспечивающий получение на выходном звене роторного двигателя вращательного движения, близкого к равномерному, или (в линейном двигателе) – получение циклического возвратно-поступательного движения. Превращение этих простейших движений в требуемые программные движения рабочих органов осуществляется исполнительными механизмами с соответствующими, как правило, нелинейными функциями положения (рычажными, кулачковыми, зубчатыми и др.). Можно сказать, что в таких машинах применяются программирующие механизмы.
Второй способ заключается в получении программных
движений рабочих органов за счет соответствующего выбора законов изменения
входных параметров двигателей ![]() , совокупность
которых образует программное управление. При этом для передачи движения от
двигателей рабочим органам могут быть использованы механизмы как с линейными,
так и с нелинейными функциями положения. Программное управление в последнее
время все более широко используется в технологических и транспортных машинах.
Часто оно осуществляется рабочим-оператором; таким способом управляются автомобили,
самолеты, подъемные краны. Вместе с тем все более широкое распространение
получают автоматы с программным управлением, в особенности промышленные роботы.
, совокупность
которых образует программное управление. При этом для передачи движения от
двигателей рабочим органам могут быть использованы механизмы как с линейными,
так и с нелинейными функциями положения. Программное управление в последнее
время все более широко используется в технологических и транспортных машинах.
Часто оно осуществляется рабочим-оператором; таким способом управляются автомобили,
самолеты, подъемные краны. Вместе с тем все более широкое распространение
получают автоматы с программным управлением, в особенности промышленные роботы.
Программное управление оказывается особенно полезным в тех случаях, когда рабочие органы машины, в зависимости от тех или иных условий, должны осуществлять различные программные движения (например, перемещать груз по различным траекториям). Переход от одного программного движения к другому сводится при этом к изменению программного управления, что в современных системах управления, использующих электронные устройства, осуществляется достаточно просто. При применении первого способа изменение программных движений связано с изменением структуры или параметров программирующего механизма, что требует, по крайней мере, переналадки механизма или замены его отдельных звеньев.
Это преимущество обуславливает широкое применение принципа программного управления в машинах, используемых для гибких автоматизированных производств, в которых необходима быстрая переналадка системы на новый рабочий процесс.
 Вместе с тем машинам с
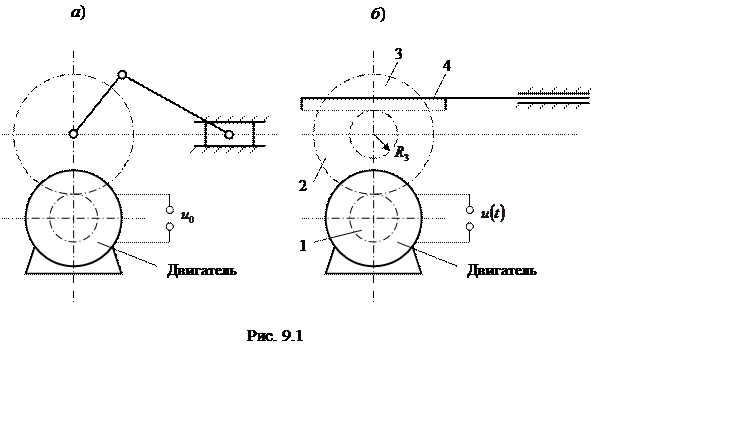
программным управлением присущи и некоторые недостатки. На рис. 9.1 приведены
схемы машинных агрегатов, в которых рабочие органы совершают
возвратно-поступательное движение. В схеме, показанной на рис. 9.1, а,
ротор двигателя вращается с постоянной угловой скоростью; преобразование этого
вращения в возвратно-поступательное движение рабочего органа (ползуна)
осуществляется программирующим кривошипно-ползунным механизмом. В схеме,
приведенной на рис. 9.1, б, на вход двигателя постоянного тока с
независимым возбуждением подается знакопеременное входное напряжение
Вместе с тем машинам с
программным управлением присущи и некоторые недостатки. На рис. 9.1 приведены
схемы машинных агрегатов, в которых рабочие органы совершают
возвратно-поступательное движение. В схеме, показанной на рис. 9.1, а,
ротор двигателя вращается с постоянной угловой скоростью; преобразование этого
вращения в возвратно-поступательное движение рабочего органа (ползуна)
осуществляется программирующим кривошипно-ползунным механизмом. В схеме,
приведенной на рис. 9.1, б, на вход двигателя постоянного тока с
независимым возбуждением подается знакопеременное входное напряжение ![]() , вызывающее реверсивное движение
ротора, которое с помощью зубчатой передачи и зубчато-реечного механизма
преобразуется в возвратно-поступательное движение выходного звена – зубчатой
рейки; таким образом, в этой схеме используется принцип программного
управления.
, вызывающее реверсивное движение
ротора, которое с помощью зубчатой передачи и зубчато-реечного механизма
преобразуется в возвратно-поступательное движение выходного звена – зубчатой
рейки; таким образом, в этой схеме используется принцип программного
управления.
Сравнивая эти схемы, легко заметить преимущество системы с программным управлением в том случае, если, например, необходимо изменить величину хода рабочего органа. В первой схеме этот ход равен удвоенной длине кривошипа, и для его изменения необходимо изменение этой длины, что требует переналадки механизма. Рассмотрим, каким образом изменение хода достигается во второй схеме. Предположим, что для двигателя может быть выбрана идеальная характеристика (8.5), а входное напряжение изменяется по гармоническому закону
![]() , (9.1)
, (9.1)
Подставляя (9.1) в (8.5), получаем
![]() .
.
Интегрируя это выражение и полагая, что при ![]()
![]() ,
находим
,
находим
![]() . (9.2)
. (9.2)
Отсюда легко определить закон движения выходного звена:
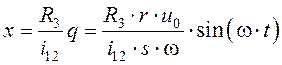 , (9.3)
, (9.3)
где ![]() –
передаточное отношение зубчатой передачи, а
–
передаточное отношение зубчатой передачи, а ![]() –
радиус начальной окружности зубчатого колеса 3. Из выражения (9.3) видно, что
ход рейки
–
радиус начальной окружности зубчатого колеса 3. Из выражения (9.3) видно, что
ход рейки
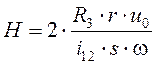 , (9.4)
, (9.4)
и для его изменения
достаточно изменить напряжение ![]() .
.
С другой стороны, легко заметить, что отклонение хода от его номинальной величины в первой схеме зависит только от точности выполнения длины кривошипа и не зависит от каких-либо других параметров системы. Во второй схеме величина хода зависит от многих параметров
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.