Расчет плоского кулачкового механизма. Силовой расчет червячной передачи

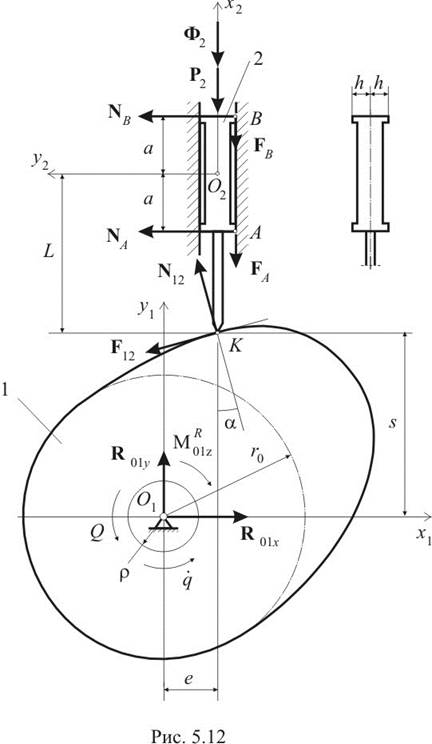
Рассмотрим плоский кулачковый механизм с поступательно движущимся толкателем (рис. 5.12). Ограничимся определением компонент реакций, действующих в плоскости движения. Уравнения кинетостатики, составленные для толкателя и кулачка, разделяются и могут решаться независимо. Составим уравнения кинетостатики для толкателя. Силы, действующие на толкатель со стороны кулачка, сводятся к силе , направленной по нормали к профилю кулачка в рассматриваемом положении, и силе трения . Выберем модель поступательной пары с двухточечным контактом; силы ,  и соответствующие силы трения  и  действуют на толкатель со стороны стойки. Введем систему координат 0₂x₂y₂, связанную с толкателем; в результате получаем уравнения кинетостатики в следующем виде:

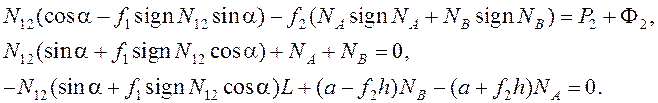    (5.27)

Здесь α и f₁ – соответственно угол давления и коэффициент трения в высшей кинематической паре К, f₂ – коэффициент трения в поступательной паре, P₂ – рабочая нагрузка, Ф₂ – сила инерции толкателя, а, h, L – геометрические параметры, обозначенные на рисунке. Силы P₂ и Ф₂ считаются положительными, если они направлены так, как они показаны на рисунке.

Система уравнений (5.27) является нелинейной: в ней присутствуют функции signN₁₂, signN_A, signN_B, имеющие разрывы при N₁₂=0, N_A=0, N_B=0. Уравнения станут линейными, если задать знаки неизвестных реакций. Предварительно выберем знаки N₁₂, N_A, N_B такими, какими они получились бы в рассматриваемом положении механизма, если бы силы трения отсутствовали. Полагая f₁ = 0, f₂ = 0, получаем:

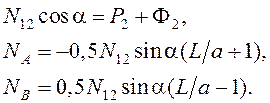
При заданном направлении сил P₂ и Ф₂ (эти силы прижимают толкатель к профилю кулачка) получаем N₁₂ > 0, N_A < 0, N_B > 0 (если L > a). Подставив в уравнения кинетостатики signN₁₂ = 1, signN_A = –1, signN_B = 1, приходим к системе линейных уравнений

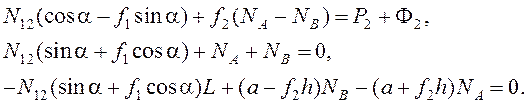          (5.28)

Из последних двух уравнений находим N_A и N_B:

  (5.29)

Если L > a + f₂ h , то при N₁₂ > 0 будет действительно N_A < 0 и N_B > 0. Подставим N_A и N_B в первое уравнение (5.28) и найдем из него реакцию N₁₂:

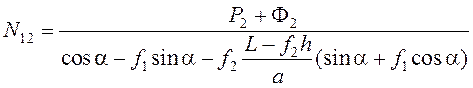.                 (5.30)

Если Р₂ + Ф₂ > 0, то реакция N₁₂ останется положительной в системе с трением при выполнении условия

.             (5.31)

При увеличении угла давления α или коэффициентов трения f₁ и f₂ значение σ уменьшается; при cosα = f₁sin α, т.е. при ctg α = f₁ она наверняка становится отрицательной. С уменьшением σ увеличивается значение |N₁₂|, при σ = 0 реакция становится «бесконечно большой», что свидетельствует о заклинивании механизма. Значения σ, при которых N₁₂ < 0, вообще не должны рассматриваться, поскольку такое решение не удовлетворяет тем условиям, при которых были получены уравнения (5.28). Могут ли исходные уравнения (5.27) иметь решение, в котором N₁₂ < 0 при Р₂ + Ф₂ > 0? Если при этом принять, что N_A>0, N_B<0, то из (5.27) получаем

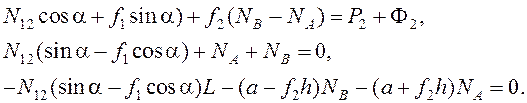        (5.32)

Из последних двух уравнений находим:

  (5.33)

Полагая, что N₁₂ < 0, sin α > f₁cos α  (сtg α < f₁), получаем, действительно, N_A > 0, N_B < 0. Подставив (5.33) в первое уравнение (5.32), имеем:

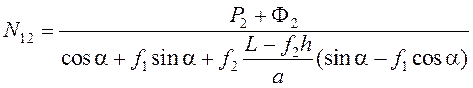.                   (5.34)

Это уравнение, а следовательно, и исходная система не может иметь решение N₁₂ < 0 при Р₂ + Ф₂ > 0, какими бы ни были значения α и f₂. Таким образом, при σ < 0 исходная система уравнений вообще не имеет решений, если Р₂+Ф₂>0.

Пусть Р₂ + Ф₂ < 0, т.е. предположим, что направление суммарной силы совпадает с направлением скорости толкателя . Может ли система уравнений (5.27) иметь при этом решение, в котором N₁₂ > 0, N_A < 0, N_B > 0? Если L > a + f₂h, то для определения N₁₂ вновь получаем выражение (5.30), из которого следует, что при σ < 0 и Р₂ + Ф₂ < 0 будем иметь N₁₂ > 0, а тогда в силу соотношений (5.29) имеем N_A < 0, N_B > 0.

Таким образом, при выполнении условия σ < 0 движение возможно, если сумма рабочей нагрузки и силы инерции направлена по скорости, т.е. играет роль движущей силы. Это – режим оттормаживания, о котором уже говорилось ранее.

Возможно и другое решение, в котором N₁₂ < 0, N_A > 0, N_B < 0. Действительно, при таких знаках реакций мы приходим к уравнениям (5.32), а затем – к выражению (5.34), из которого при Р₂ + Ф₂ < 0 и при ctg α > f₁ получается второе решение N₁₂ < 0, поскольку выражение, стоящее в знаменателе, в этом случае положительно.

Существование двух режимов оттормаживания легко объяснить: в первом