Расчет величин для определения параметров уравнения регрессии и тесноты связи. Уравнение прямолинейной корреляционной зависимости заработной платы от производительности труда имеет вид

Полученные результаты свидетельствуют о том, что при увеличении производительности труда работников на 1 руб. оплата труда возрастает

 на    руб.

По уравнению регрессии можно найти выравненные теоретические значения результативного признака при соответствующих значениях фактора х (табл.1). Отклонения фактических значений y от теоретических  обусловлены тем, что регрессия y строилась только по одному фактору х, в то время как в действительности y зависит от множества факторов.

Показателями тесноты корреляционной связи служат коэффициент и индекс корреляции. Теснота связи между признаками измеряется с помощью показателей вариации результативного признака y.

Чтобы измерить, насколько связь близка к функциональной, исчисляют показатели тесноты связи. Для этого необходимо оценить вариацию результативного признака y, вызванную только влиянием признака х, и остаточную его вариацию, обусловленную прочими факторами.

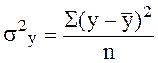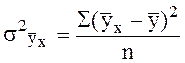Общая дисперсия результативного признака  характеризует вариацию y под влиянием всех факторов. Средний квадрат отклонений  от    измеряет вариацию y только под влиянием фактора х – это факторная дисперсия. Средний квадрат отклонений y от   = S(y–)²/n характеризует остаточную вариацию y под влиянием всех остальных факторов. В математической статистике доказано, что s²_y = , т.е. . Поэтому эту дисперсию называют остаточной дисперсией, она характеризует вариацию y за счет остальных факторов, не включенных в уравнение регрессии.

Теснота связи между y и х измеряется отношением факторной дисперсии к общей дисперсии результативного признака, называемым индексом детерминации, . Индекс детерминации характеризует долю вариации результативного признака под влиянием факторного признака в общей колеблемости результативного признака.

Если между признаками имеется корреляционная связь, то по мере ее усиления, т.е. повышения тесноты связи между результативным и факторным признаками, индекс детерминации увеличивается, а по мере ослабления – уменьшается. Таким образом, индекс детерминации характеризует тесноту связи, близость корреляционной связи к функциональной.

Корень квадратный из индекса детерминации есть индекс корреляцииили теоретическое корреляционное отношение

.

Индекс корреляции показывает тесноту связи между результативным и факторным признаками при любой форме связи. Если линия регрессии совпадает с эмпирическими данными, т.е. = s_y и h = 1, то между признаками имеет место полная связь. Если = 0, т.е. изменения х не вызывают изменений y, то h =0 и связь между признаками отсутствует.

Индекс корреляции  рассчитаем исходя из общей и остаточной дисперсии производительности труда:

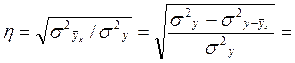
Значение индекса корреляции свидетельствует о весьма тесной связи между оплатой труда и выработкой работников почтовой связи. Индекс детерминации показывает, что  вариации заработной платы объясняется вариацией производительности труда.

Значения индекса корреляции и эмпирического корреляционного отношения почти совпадают, поскольку отражают одну и ту же сущность оценивания тесноты связи между результативным и факторным признаками.

Частным случаем индекса корреляции является линейный коэффициент корреляции r, который применяется для оценки тесноты связи при линейной зависимости. Линейный коэффициент корреляции строится на сопоставлении отклонений коррелируемых признаков от их средних арифметических (х–) и (y–). Чтобы обеспечить соизмеримость отклонений признаков х и y по абсолютным размерам и единицам измерения, рассчитывают их нормированные отклонения:

t_x = (x–)/s_x;  t_y = (y–)/s_y , где s_x, s_y – средние квадратические отклонения признаков х и y.

Рассчитаем линейный коэффициент корреляции:

Получен тот же результат, что и в расчете индекса корреляции