Понятие информационной системы. Этапы развития Информационных систем. Этапы развития. Состав современной клиент-серверной информационной системы, страница 11

Для такой сети можно составить окончательную систему уравнений:

К предыдущей системе добавится

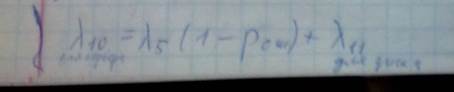
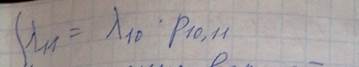
Рош-?

Предположим линейную модель ошибки в среде передачи. Тогда с вероятностью Ре имеет место искажение любого бита информ. Данная величина постоянна и не зависит от отсутсвия или наличия ошибок в других битах. Обычно эта величина лежит в пределао от 10в минус 4ойдо 10 в минус 7ой. Если принять среднее значение Р0  10 в минус 5ой, то вероятность того, что пакет длиною Q бит будет иметь ошибку мб вычеслина по формуле

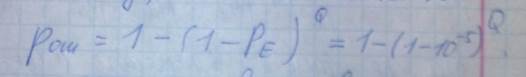
По скольку длина пакета известна в сети, следовательно и величина Рош тоже может считаться известной и передаваться в систему уравнений потоков в качестве коэфицентов.

Рст-?

Также предположим пуассоновский процесс передачи пакетов в среде передачи.

Тогда вероятность начала передачи пакета за время Ƭ, те за время распределения уже переданного пакета, что приводит к столкновению пакетов и конфликту, будет равна

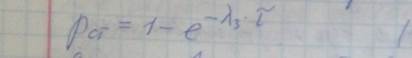
Следовательно выраж,мб включено в систему.

Рзс-?

Вероятность события, состоящего в том, что в момент передачи среда передачи занята, есть по определению загрузка среды передачи. Тогда для этой вероятности можно записать

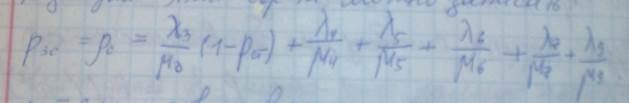
S8 не участвует в передаче пакета , µ известна .

Вычислим λ0Вход в сеть создается сетевыми операциями техпроцессов, в нашем случае это 1-е и 3-е первого техпроцесса и 2-я операция второго техпроцесса., те можно записать:

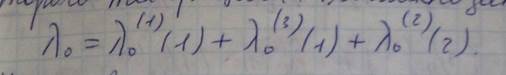
Нужно вычислить

29. Расчет времени цикла технологического процесса оператора локальной сети с методом доступа CSMA/CD

Интенсивность поступления заявок от какой – либо операции техпроцесса – есть велична обратная времени цикла данного техпроцесса, относительно этой операции. Время цикла ТП типа i относительно операции j называется время между двумя последовательными входами в эту операцию. Каждый ТП имеет столько времен циклов, сколько и операций. Если ТП линейный, то времена циклов одинаковые. Времена циклов явл случайными величинами.

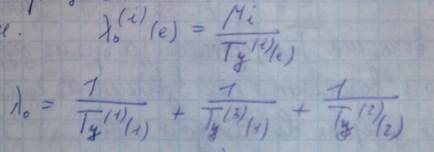
Времена циклов вычисляются через коэфиценты передач. Будем считать, что все ТП создают одинаковые запросы, для вычисления времени цикла необходимо складывать времена выполнения операции, а для сетевых операций прибавлять время сети, кот. Во всех случаях будет одинаковое.

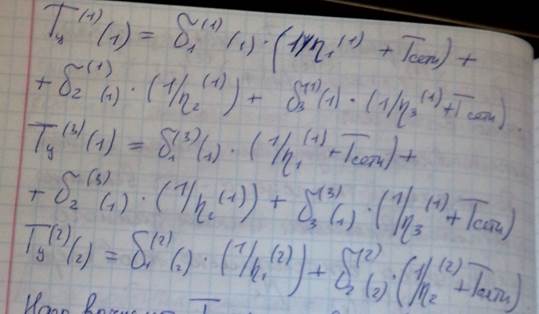
Надо вычислить Тсети, а время задержки в сети вычисляется как взвешенная сумма вемен задержек во всех узлах сети.

Запросы одинаковы. Время нахождения заявки СеМО складывается. А время нахождения заявки в узле, те СМО, складывается из времени ожидания в очереди и времени обслуживания. Тк в нашей Семо большинство узлов представляют собой СМО без очередей, то для них время ожидания в очереди = 0

Выражение для Тсети получено. ,следовательно вся система уравнений получена.

Выпишим окончательный вариант системы для нахождения вероятносных характеистик ЛВС с методом доступа CSMA/CD для примера из 2-х ТП

Решив, мы получим необходимые исх. Данные для расчета вероятностных характеристик.

Интересует время решения задачи, иногда время работы сети. Поскольку любой ТП в жизни начинается с операции, то время решения задачи есть время цикла, относительно 1ой операции. Если 1я операция сетевая, то это время цикла необх. Вычислять дополнительно, в нашем случае так обстоит дело со 2ТП. В этом случае необходимо вычислить коэфиценты передач относительно первой операции. Для этого ТП, а это значит вычислить время цикла, подставив туда найденное из системы уравнений значение Тсети, Т1- из системы уравнений, Т2:

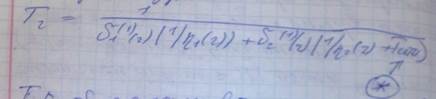
Общая последовательность этапов для нахождения вероятностно – временных характеристик ЛВС:

1.  Вычислить коэф. Передач относительно всех сетевых операций всех ТП

2.  Вычислить среднее время обслуживания во всех узлах модели(1/µ)

3.  Вычислить значение Ƭ

4.  Вычислить Рош

5.  Составить и рассчитать систему уравнений

6.  Если 1я операция ТП сетевая, то взять время решения задачи для этого ТП из системы уравнений, как время цикла, относительно 1ой операции. Если 1я операция несетевая, то вычислить для нее коэфиценты передач, а затем вычислить Тцикла относительно этой операции. Используя найденное в системе уравнений Тсети.