Эконометрическая модель, характеризующая зависимость между чистым доходом и объемом капиталовложений, страница 2

На основе взаимной корреляционной функции установлено, что цепь капиталовложений равна 1, то есть через 1 год после инвестирования можно получить наибольший прирост чистого дохода.

Решение

1)  Идентификация переменных и спецификация модели.

У – чистый доход, зависимая переменная;

Х – объем капиталовложений, пояснительная переменная.

Эконометрическая модель имеет вид:

У_t = f(x₁);

У_t  = a₀ + a₁ x_t-1 + u_t; (u_t – стохастическая составляющая);

У_t = a₀ + a₁ x_t-1 – линейная функция.

2)  Оценка параметров модели.

Так как цепь капиталовложений = 1 год, то исходные данные будут сокращены на 1 наблюдение, причем во временном ряду чистого дохода будет отброшено первое наблюдение, а во временном ряду капиталовложений – одно последнее наблюдение.

Матрица независимых переменных размером n^xm (n – число наблюдений, m – количество независимых переменных) имеет следующий вид:

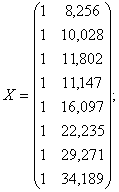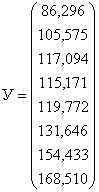Матрица У – вектор значений зависимой переменной.

Для определения вектора параметров модели найдем оценку параметров модели.

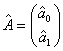где Â = В^-1 * (Х^т * У),

Х^т – транспонированная матрица:

Перемножим матрицу Х^т на матрицу У, получим результат: