Определенная по (4.6) величина не дает ответа на вопрос, каков тип поляризации светового пучка. Поэтому на практике часто используется другая характеристика, основанная на анализе света, прошедшего через поляризатор. Измеряется интенсивность прошедшего света при вращении поляризатора вокруг направления светового пучка. Определяются максимальная Imax и минимальная Imin интенсивности (соответствующие двум ортогональным ориентациям поляризатора) и вычисляется величина D по формуле
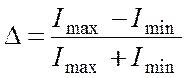 (4.7)
(4.7)
Вычисленный таким образом параметр D лежит в пределах 0 £ D £ 1. Значение D = 1 соответствует линейно поляризованному свету (при определенном положении поляризатора свет полностью гасится), а значение D = 0 – естественному или циркулярно поляризованному свету (интенсивность прошедшего света не зависит от положения поляризатора). Величина D представляет по сути степень линейной поляризации, ее удобно использовать при анализе света, отраженного от границы раздела оптических сред (см. раздел 5.2).
Поскольку как поляризация, так и когерентность света непосредственно определяются поведением фазы электромагнитной волны, встает вопрос о соотношении степени поляризации и степени когерентности света. Хаотическое изменение фазы излучения обычных источников белого света приводит к появлению некогерентного и неполяризованного излучения. С помощью поляризаторов это излучение может быть сделано линейно, циркулярно или эллиптически поляризованным без изменения его спектрального состава. В результате получается поляризованный, но некогерентный свет.
С другой стороны, монохроматизация белого света, реализуемая изотропными абсорбционными или интерференционными светофильтрами, не влияет на его состояние поляризации – свет может стать квазимонохроматическим, но остаться неполяризованным.
Таким образом, непосредственной связи между степенью поляризации и степенью когерентности нет. Заблуждения на этот счет часто появляются в результате знакомства с предельно когерентным излучением лазерных источников с линейной поляризацией (например, гелий-неонового лазера). При этом поляризация определяется как сохранением ориентации вектора E при вынужденном излучении, так и особенностями конструкции лазера (брюстеровскими окнами в резонаторе, см. раздел 5.2). Если же расположить выходные окна перпендикулярно оптической оси лазера, поляризационные свойства излучения оказываются совершенно иными. С другой стороны, короткоимпульсные лазеры могут давать свет полностью поляризованный, но с весьма низкой степенью когерентности.
Описание состояния полностью поляризованного света может основываться непосредственно на параметрах эллипса поляризации, как наиболее общего случая сложения двух ортогональных колебаний с одинаковой частотой. Если разворотом системы координат совместить ее оси с полуосями эллипса (рис. 4.6), то величина tgc называется эллиптичностью, а угол y – азимутом. Состояние поляризации часто обозначают с помощью т. н. вектора Стокса, четыре компоненты которого имеют размерность интенсивности и могут быть измерены экспериментально:
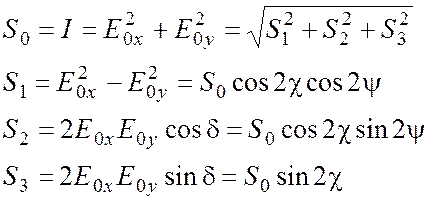 . (4.8)
. (4.8)
Параметр S0 равен полной интенсивности светового пучка; S1 представляет преобладание горизонтальной линейной поляризации (вдоль оси X) над вертикальной (вдоль оси Y); S2 – преобладание линейной поляризации под углом 45о над поляризацией под углом 135о; S3 – преобладание правой круговой поляризации над левой.
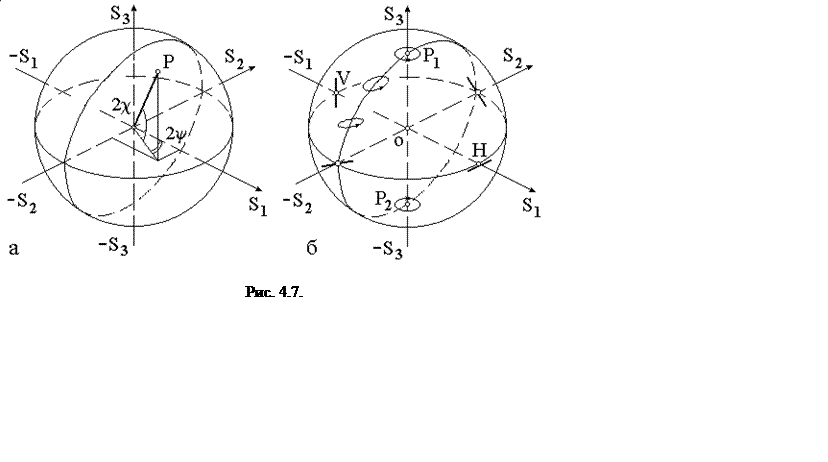 |
На полюсах сферы Пуанкаре расположены две циркулярные поляризации, на экваторе – линейные поляризации всех азимутов. Параллели являются линиями равной эллиптичности (“широта места” равна 2c), а меридианы – линиями равных азимутов (“долгота места” равна 2y) (рис. 4.7б). Если передвигаться по одному выбранному меридиану от верхнего полюса к нижнему, то в верхнем полушарии мы пройдем последовательно через все более вытянутые эллипсы с правым вращением электрического вектора и на экваторе попадем в точку, характеризующую линейную поляризацию с азимутом, равным азимуту больших полуосей эллипсов. В нижнем полушарии направление вращения сменится на противоположное.
Описание с помощью параметров
Стокса применимо и для частично поляризованного света. В этом случае ![]() , а степень поляризации
, а степень поляризации
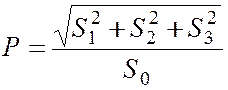 (4.9)
(4.9)
совпадает с определением (4.6).
Параметры Стокса часто записывают в матричном виде как вектор-столбец из четырех компонент. Некоторые примеры векторов Стокса приведены ниже:
|
|
|
|
|
|
|
естеств. свет |
линейная вдоль OX |
линейная вдоль OY |
Линейная под углом 45о |
правая круговая |
При прохождении света через различные оптические приборы состояние поляризации может изменяться. Поляризационные характеристики устройства характеризуются с помощью матрицы Мюллера, которая связывает входной и выходной вектора Стокса:
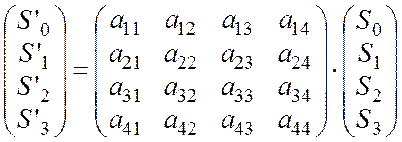 , (4.10)
, (4.10)
где 16 коэффициентов aij зависят от конкретного типа устройства. Так, например, поляризатор с пропусканием вдоль оси X описывается матрицей
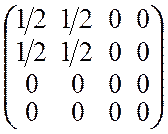 .
.
Действительно, если эту матрицу умножить на вектор Стокса, соответствующий произвольной поляризации, получим вектор линейно поляризованного света:
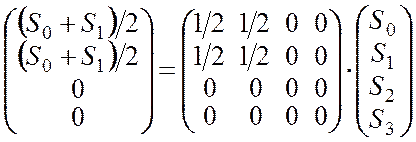 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.