Сопротивление ветвей. Узловые напряжения и токи в ветвях с использованием метода Гаусса с обратным ходом

Задача №1

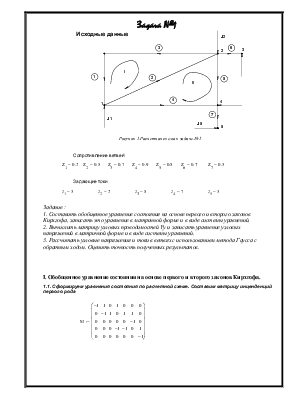
Исходные данные

Рисунок 1.Расчетная схема к задаче №1

Сопротивление ветвей

Задающие токи

Задание :

1. Составить обобщенное уравнение состояния на основе первого и второго законов Кирхгофа, записать это уравнение в матричной форме и в виде системы уравнений.

2. Вычислить матрицу узловых проводимостей Yy и записать уравнение узловых напряжений в матричной форме и в виде системы уравнений.

3. Рассчитать узловые напряжения и токи в ветвях с использованием метода Гаусса с обратным ходом. Оценить точность полученных результатов.

I. Обобщенное уравнение состояния на основе первого и второго законов Кирхгофа.

1.1. Сформируем уравнения состояния по расчетной схеме. Составим матрицу инценденций первого рода

1.2. Составим матрицу инценденций второго рода

1.3. Найдем произведение матрицы инценденций второго рода и матрицы сопротивлений

=

1.4. Объединенная матрица коэффициентов

1.5. Вектор ЭДС контуров имеет вид:

т.к. ЭДС в контурах отсутствует.

1.6. Объединенная матрица свободных членов имеет вид:

1.7. Обобщенное уравнение состояния ЭС:

=

=

II. Матрица узловых проводимостей и уравнение узловых напряжений.

2.1. Составим транспонированную матрицу инценденций первого рода

2.2. Определяем матрицу узловых проводимостей

=

2.3. В матричной форме уравнение узловых напряжений имеет вид:

=

2.4. Составим систему уравнений узловых напряжений:

8.111 UD1                -2 UD2                               -1.111 UD4                                     = 3

-2 UD1          6.857 UD2         -1.429 UD3            -2 UD4                                    = 2

-1.429 UD2           1.429 UD3                                                           = 5

-1.111 UD1                 2 UD2                                      6.444 UD4       -3.333 UD5      = 7

-3.333 UD4        3.333 UD5      = 3

III. Расчет узловых напряжений и токов в ветвях с использованием метода Гаусса с обратным ходом. Оценка полученных результатов.

3.1. Получим первое ключевое уравнение, для чего разделим первое уравнение системы на коэффициент при UD1 (2), а затем исключим UD1 из всех уравнений ниже ключевого:

UD1          -0.247  UD2                                  -0.137  UD4                            =  0.370

6.364 UD2           -1.429 UD3      -2.274 UD4                              =  2.740

-1.429 UD2            1.429 UD3                                                      =  5.000

-2.274 UD2                                  6.292 UD4        -3.333 UD5      =  7.411

-3.333 UD4        3.333 UD5      =  3.000

3.2. Получим второе ключевое уравнение, для чего разделим второе уравнение системы на коэффициент при UD2 (1,38), а затем исключим UD2 из всех уравнений ниже ключевого:

UD1              -0.247  UD2                                 -0.137 UD4                             =  0.370

UD2        -0.255 UD3       -0.357 UD4                             =  0.413

1.108 UD3      -0.511 UD4                              =  5.615

-0.511 UD3       5.479 UD4        -3.333 UD5    =  8.390

-3.333 UD4        3.333 UD5     =  3.000

3.3. Получим третье ключевое уравнение, для чего исключим UD3 из всех уравнений ниже ключевого:

UD1              -0.247  UD2                               -0.137 UD4                               =  0.370

UD2           -0.255 UD3      -0.357 UD4                              =  0.413

UD3      -0.461 UD4                              =  5.068

5.244 UD4        -3.333 UD5     = 10.980

-3.333 UD4        3.333 UD5      =  3.000

3.4. Получим четвертое ключевое уравнение, для чего исключим UD4 из последнего уравнения.

UD1              -0.247  UD2                                 -0.137 UD4                               =  0.370

UD2           -0.255 UD3        -0.357 UD4                              =  0.413

UD3       -0.461 UD4                              =  5.068

UD4        -0.636 UD5    =  2.094

1.215 UD5    =  9.978

3.5. Получим пятое ключевое уравнение, для чего исключим UD5 из последнего уравнения:

UD1              -0.247  UD2                                   -0.137 UD4                            =  0.370

UD2           -0.255 UD3      -0.357 UD4                           =  0.413

UD3      -0.461 UD4                           =  5.068

UD4        -0.636 UD5  =  2.094

UD5  =  8.213

3.6. Обратный ход Гаусса:

3.7. Проведем анализ точности расчета, для чего проведем расчет невязок по исходной системе:

3.8. Из уравнения связи параметров режима находим падения напряжений