




















Оптимизационные модели и методы в задачах электроэнергетики
Методические указания
к выполнению лабораторных работ по курсу
«Методы оптимизации в СЭС» для студентов ФЭН
дневной и ускоренной форм обучения
Новосибирск
2003
Составители: , канд. техн. наук, доц.
, канд. техн. наук, доц.
Рецензент , д-р техн. наук, проф.
Работа подготовлена на кафедре систем электроснабжения
Оглавление
Введение. 4
1. Модели и методы линейного программирования.. 4
1.1 Описание лабораторной работы №1. 4
1.1.1 Порядок выполнения лабораторной работы: 5
1.1.2 Варианты задания. 5
1.1.3 Контрольные вопросы.. 7
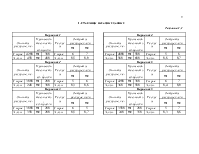
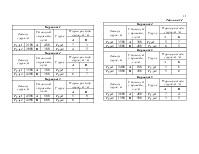
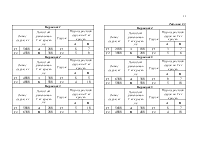
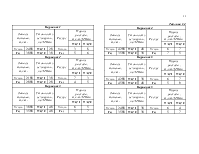
1.2 Таблицы исходных данных. 8
2. Модели и методы нелинейного программирования.. 16
2.1 Описание лабораторной работы №2. 16
2.1.1 Порядок выполнения лабораторной работы: 16
2.1.2 Варианты задания. 16
2.1.3 Контрольные вопросы.. 18
1.2 Таблицы исходных данных. 18
3. Математические модели оптимизации развития энергосистем... 21
3.1 Описание лабораторной работы №3. 21
3.1.1 Порядок выполнения лабораторной работы: 21
3.1.2 Варианты задания. 21
3.2 Описание лабораторной работы №4. 21
3.2.1 Порядок выполнения лабораторной работы: 21
3.2.2 Варианты задания. 22
3.2.3 Контрольные вопросы.. 22
3.3 Таблицы исходных данных. 23
В настоящее время накоплен богатый опыт применения методов математического моделирования, в частности, для решения оптимизационных задач управления и развития сложных систем энергетики. Модели и методы оптимизации успешно внедряются в практику планирования, проектирования и эксплуатации электроэнергетических систем.
Режимные вопросы управления системами, построение схем и выбора структур электрических сетей, выбора мощности, типа и очередности сооружения электрических станций, оптимизации систем электроснабжения потребителей с учетом качества электроэнергии, компенсации реактивной мощности и многие другие задачи часто ставятся и разрешаются как математические экстремальные при определенных ограничениях, т.е. как задачи исследования операций. В связи с этим, в электроэнергетике большое распространение и влияние получили идеи и методы математического оптимального программирования. Под математическим программированием понимается построение или управление объектами или их совокупностями по некоторым признакам цели с ограничениями по разным условиям. С математической точки зрения, каждая задача сводится, как правило, к отысканию наименьших (наибольших) значений некоторой функции конечного числа переменных или функционала при наличии ограничений в форме уравнений и неравенств, которые отражают физические и технологические особенности объекта моделирования.
Изучение оптимизационных задач электроэнергетики составляет основу данного курса, в котором рассматриваются модели и методы исследования операций, в частности линейного, нелинейного программирования, многоцелевой оптимизации и т.д. Особое внимание уделено применению современных методов компьютерного моделирования на основе широко используемых в практике программных систем Mathcad и Microsoft Excel.
В данной работе представлены методические указания и варианты исходных данных для выполнения лабораторных работ по курсу "Методы оптимизации в СЭС". Материал пособия предназначен для студентов обычной и ускоренной дневной формы обучения специальности 100400 – электроснабжение факультета энергетики.
Цель работы: знакомство с основными типами задач линейного программирования, а также получение практических навыков решения задач оптимизации с помощью основных методов линейного программирования и реализации этих методов в среде Mathcad и Microsoft Excel.
1. Составить математические модели задач, исходя из содержательной постановки, заполнить типовую таблицу по исходным данным задачи;
2. Решить задачу графическим методом в среде Mathcad;
3. Решить задачу методом перебора вершин в среде Mathcad;
4. Решить задачу с помощью надстройки «Поиск решения» среды Microsoft Excel.
Для выполнения лабораторной работы в качестве исходных данных студенту выдаются 2 задачи:
· Задача 1 линейного программирования (количество переменных n = 2) для выполнения пунктов 1, 2, 3 задания.
· Задача 2 линейного программирования (количество переменных n = 4) для выполнения пунктов 1, 4 задания.
Шифр для задачи 1 и задачи 2 задается преподавателем отдельно по вариантам, например 1 . 1.
Шифр состоит из двух цифр:
1 цифра / 2 цифра
{№ условия задачи} {№ варианта числовых значений для задачи}
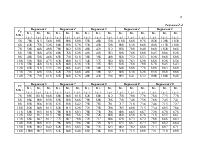
Ø Исходные данные для решения задачи 1 графическим методом и методом перебора вершин в среде Mathcad.
В начале выбирается условие задачи (1 цифра варианта), а затем числовые значения из соответствующей таблицы (2 цифра варианта).
Условие № 1
На промышленном предприятии реализован непрерывный технологический процесс производства продукции, который включает в себя использование двух различных технологий: Т1 и Т2. В процессе производства наиболее существенную роль играют два вида ресурсов: сырье и электроэнергия. Известны затраты каждого вида ресурса при работе по технологиям Т1 и Т2, а также запас сырья и лимит по электроэнергии. Известен выпуск продукции по технологиям за час работы. Определить оптимальное распределение времени работы предприятия по каждой технологии, которое обеспечивает максимальный выпуск продукции. Численные значения приведены в таблице 1.1.
Условие №2
Для производства двух видов проката А и В используется два сорта руды, причем закупки сырья ограничены возможностями поставщиков. Известна цена 1т каждого вида проката, а также норма расхода сырья на 1т проката и ограничения на запасы сырья. Найти оптимальный план производства проката, при котором обеспечивается максимальная прибыль от его реализации, если известна прибыль от реализации единицы продукции, т.е. 1 т проката вида А и В.
Численные значения приведены в таблице 1.2
Условие №3
Цех промышленного предприятия выпускает 2 типа краски для внутренних (А) и наружных (В) работ. Для производства красок требуется 2 вида сырья (С1 и С2), запасы сырья определяются возможностями поставщиков. Известен доход от реализации 1 кг краски каждого типа. Необходимо составить оптимальный план производства красок обоих
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.