Модели и методы одноцелевой оптимизации. Задача оптимального распределения нагрузки между ТЭС энергосистемы

таком подходе основан в частности метод предпочтений (метод последовательных уступок), который рассматривается в курсовой работе на примере планово-производственной экономической двухкритериальной задачи линейного программирования.

Варианты задания

Условие № 1

Цех промышленного предприятия выпускает две марки раствора. Известно соотношение цемента и песка для каждой марки раствора. Запасы сырья определяются возможностями поставщиков.

Составить оптимальный план производства раствора всех марок с позиций многоцелевой оптимизации, при котором объем реализации раствора будет максимальным (в стоимостном выражении) и качество раствора также будет наилучшим, если известна цена 1 т раствора.

Численные значения приведены в Приложении 5 (табл. П5.1).

Условие № 2

Для производства двух видов проката А и В используется два сорта руды, причем закупки сырья ограничены возможностями поставщиков. Известны цена 1 т сырья и 1 т каждого вида проката, а также нормы расхода сырья на 1 т проката вида А и В, запасы сырья.

Определить оптимальный с позиций многоцелевой оптимизации план производства проката, при котором обеспечивается максимальный объем реализации (в стоимостном выражении) и наилучшее качество проката.

Численные значения приведены в Приложении 5 (табл. П5.2).

Условие № 3

На промышленном предприятии реализован технологический процесс производства продукции, который включает в себя использование двух различных технологий Т1 и Т2. В процессе производства наиболее существенную роль играют два вида ресурсов: сырье и электроэнергия. Известны затраты каждого вида ресурсов при работе по технологиям Т1 и Т2, а также лимиты по сырью и электроэнергии, количество продукции, выпускаемой в единицу времени при работе по технологиям Т1 и Т2.

Численные значения приведены в Приложении 5 (табл. П5.3).

Выполнение данного раздела курсовой работы включает в себя следующие этапы:

Ø Решение задачи многоцелевой оптимизации без применения ЭВМ с целью освоения алгоритма метода предпочтений

Порядок выполнения

·  Заполнить типовую таблицу по исходным данным задачи, ввести обозначения оптимизируемых переменных;

·  На первом этапе предпочтение отдается объему V как основной характеристике производства. При этом необходимо составить математическую модель, исходя из содержательной постановки, когда первый критерий V выступает в качестве целевой функции, а второй К – в виде ограничений:

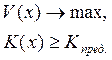                                    (2.1)

·  На втором этапе предпочтение отдается качеству К как одной из наиболее важных характеристик производства. При этом необходимо составить математическую модель, исходя из содержательной постановки, когда первый критерий К выступает в качестве целевой функции, а второй V – в виде ограничений:

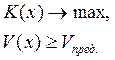                                   (2.2)

·  Решить задачу для обоих случаев с помощью графического метода линейного программирования;

·  С учетом полученных результатов построить кривую компромиссных решений.

Ø Решение задачи многоцелевой оптимизации с использованием надстройки  «Поиск решения» среды Microsoft Excel с целью освоения особенностей реализации моделей и методов многоцелевой оптимизации на ЭВМ.

Порядок выполнения

·  Заполнить типовую таблицу по исходным данным задачи, ввести обозначения оптимизируемых переменных;

·  На первом этапе предпочтение отдается объему V как основной характеристике производства. При этом необходимо составить математическую модель, исходя из содержательной постановки, когда первый критерий V выступает в качестве целевой функции, а второй К – в виде ограничений (2.1);

·  На втором этапе предпочтение отдается качеству К как одной из наиболее важных характеристик производства. При этом необходимо составить математическую модель, исходя из содержательной постановки, когда первый критерий К выступает в качестве целевой функции, а второй V – в виде ограничений (2.2);

·  Записать полученные математические модели в текстовом режиме, а также для решения в Microsoft Excel с помощью ссылок на ячейки;

·  С помощью надстройки «Поиск решения» в среде Microsoft Excel провести расчеты для обеих моделей. Результаты свести в таблицу и упорядочить по возрастанию;

·  С учетом полученных результатов построить кривую компромиссных решений (использовать точечный тип диаграммы со значениями, соединенными сглаживающими линиями).

Варианты задания

Шифр для задачи многоцелевой оптимизации задается преподавателем