Определяем потери активной мощности для каждого опыта j, i – дублирующих опытов:
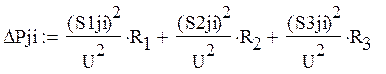
Матрица потерь мощности:
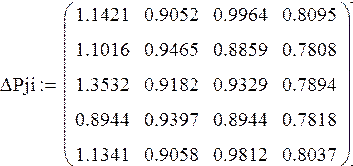
Определим выходные параметры уравнения регрессии для всех опытов:
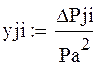
Матрица выходных параметров уравнения регрессии (матрица планирования эксперимента):
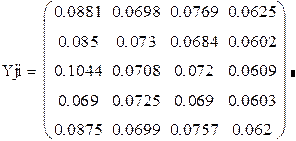
Определим среднее значение выходных параметров для каждой строки:
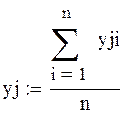
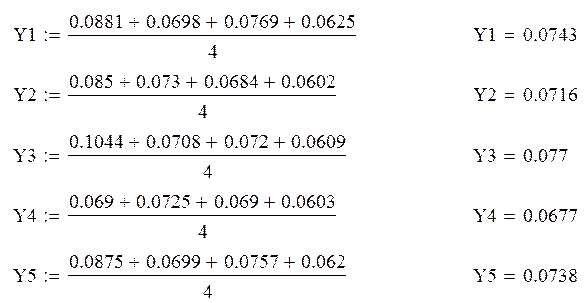
Расчётные данные будут показаны в информационной таблице.
Находим построчные дисперсии каждой строки матрицы планирования, которые характеризуют ошибку j – го опыта:
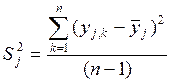
Расчётные данные будут показаны в информационной таблице.
Nопыта j |
План эксперимента ( матрица “x”) j0 j1 j2 |
Значение фактора “К” и мощности нагрузки |
“Дублирующие” опыты (n = 4) |
Среднее значение
|
Построчные дисперсии
Sj |
|||||||||||
|
X0 |
Xj |
X -a |
Кj |
Р1j |
Р2j |
yj,1 |
yj,2 |
yj,3 |
yj,4 |
|||||||
|
1 |
+1 |
-1 |
0,368 |
0,4 |
1,44 |
2,16 |
0,0881 |
0,0698 |
0,076 |
0,0625 |
0,0743 |
0,0041 |
||||
|
2 |
+1 |
+1 |
0,368 |
0,6 |
2,16 |
1,44 |
0,085 |
0,073 |
0,068 |
0,0602 |
0,0717 |
0,0039 |
||||
|
3 |
+1 |
0 |
-0,632 |
0,5 |
1,8 |
1,8 |
0,1044 |
0,0708 |
0,072 |
0,0609 |
0,077 |
0,0045 |
||||
|
4 |
+1 |
0,762 |
-0,051 |
0,5762 |
2,0743 |
1,5257 |
0,069 |
0,0725 |
0,069 |
0,0603 |
0,0678 |
0,0034 |
||||
|
5 |
+1 |
-0,762 |
-0,051 |
0,4238 |
1,5257 |
2,0743 |
0,0875 |
0,0699 |
0,075 |
0,062 |
0,0738 |
0,004 |
||||
Информационная таблица.
Проведём проверку однородности построчных дисперсий c помощью критерия Фишера:
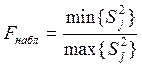
![]()
По таблице критических точек распределения Фишера – Снедекора находим критическую точку Fкр = F 0,05; n-1; n-1 = 9.28.
Сравним наблюдаемое (полученное) значение c найденной критической точкой.
Fнабл < Fкр 0,865< 9.28
Гипотеза об однородности дисперсий принимается.
Определим дисперсию ошибки всего эксперимента:
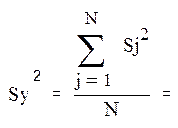
![]()
Найдём коэффициенты уравнения регрессии
|
в матричном виде
![]()
Получаем следующие значения b’o, b1, b2:
|
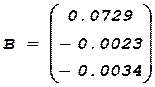
1) Оценки дисперсий
коэффициентов bi (i = 0,1,2) уравнения регрессии можно найти как
в матричном виде для общего случая, т. е.![]() , где р
– диагональная матрица с числом дублирующих опытов (в ней на месте диагональных
элементов стоят значения n (для нашего случая n=4), а остальные элементы равные
нулю получаем:
, где р
– диагональная матрица с числом дублирующих опытов (в ней на месте диагональных
элементов стоят значения n (для нашего случая n=4), а остальные элементы равные
нулю получаем:
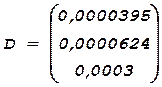
Для пересчитанного коэффициента bo оценка его дисперсии равна
![]()
![]()
Проверка значимости коэффициентов уравнения регрессии выполняется по условию
|bi| і tкрЧSbi, где tкр=t0.05,
N(n-1)=t0.05,15 = 2,13 определяется по таблицам
Стьюдента [4], а ![]() -
средние квадратичные ошибки коэффициентов bi.
-
средние квадратичные ошибки коэффициентов bi.
![]()
![]() Коэффициент bo
учитывается.
Коэффициент bo
учитывается.
Проверим коэффициент b1 :
![]()
![]() . Следовательно
коэффициент не учитывается.
. Следовательно
коэффициент не учитывается.
Проверим коэффициент b2 :
![]()
![]() . Следовательно
коэффициент не учитывается.
. Следовательно
коэффициент не учитывается.
Для перехода от уравнения регрессии y = DP = P2A ×(bo+b1x+b2x2) в кодированных значениях "x" к уравнению y = DP = P2A ×(bo+b1K+b2K2) в натуральных значениях "K" достаточно заменить в уравнении регрессии "x" на
x=(K-Ko)/ DK=(K-0,5)/0,1 . Здесь уже значения "K" изменяются в пределах от 0,4 до 0,6.
Для наглядности можно построить зависимости DP = f(K, PA), например, для трех значений K=0,4; K=0,5; K=0,6 и Ра, изменяющуюся в диапазоне от Рамин до Рамакс (из табл. 1). Для случая, когда получается значимым только один коэффициент b0 и уравнение регрессии приобретает вид DP = P2A ×b0 , эта зависимость уже не зависит от "K" и получается только одна кривая.
Построим кривую зависимости изменения потерь активной мощности:
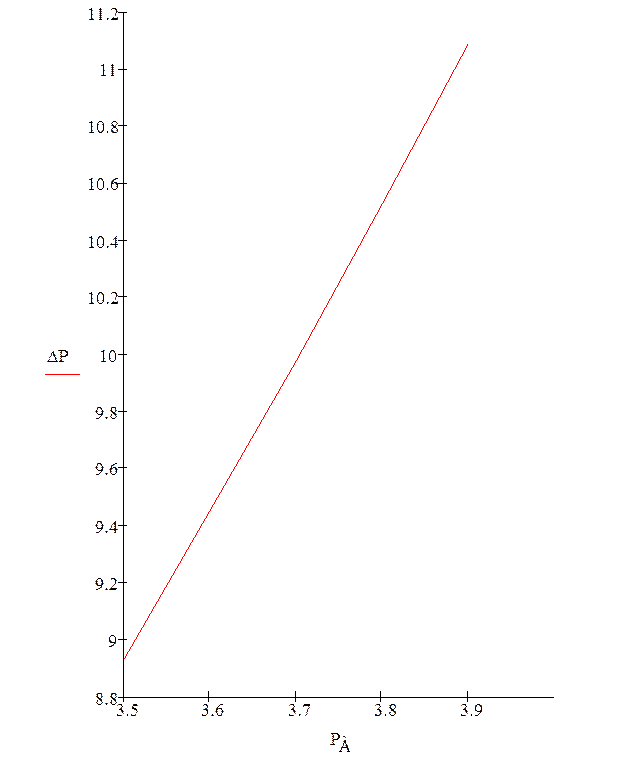 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.