Обозначения искомых переменных. Графический метод оптимизации. Применение симплекс-метода для решения задач линейного программирования

Вариант 9.

I.Задача 1

Линейного программирования (количество переменных n = 2).

Задача №3:

Для производства двух видов проката А и В используется два сорта руды, причем закупки сырья ограничены возможностями поставщиков. Известна цена 1 т проката каждого вида, а также норма расхода руды каждого вида на производство проката и имеющиеся запасы руды. Найти оптимальный план производства проката, при котором обеспечивается максимальный доход от его реализации, если известен доход фирмы от реализации 1 т проката А и В (таблица П.3).

Исходные данные для задачи 3.

Вариант 3
Запасы сырья, т.		Стоимость проката у.е./т.		Сырье	Норма расхода сырья, т/т.
					А	В
Руда 1	4500	А	500	Руда 1	5	9
Руда 2	4200	В	600	Руда 2	6	7

Введем обозначения искомых переменных:

Va – объем проката А;

Vв – объем  проката В.

Математическая модель имеет вид:

Целевая функция

F = 500×Vа + 600×Vв à max.

Система ограничений

5×Vа + 9×Vв £ 4500    (1.1)

6×Vа + 7×Vв £ 4200     (1.2)

Vа ³ 0

Vв ³ 0

Графический метод оптимизации

Отобразим графически на плоскости неравенство 5×Vа + 9×Vв £ 4500, для этого перейдем  к уравнению вида:

5×Vа + 9×Vв = 4500

Которое представим графически прямой (1) на рис. 1. по точкам (Vа=900, Vв=0) и (Vа=0, Vв=500).

Аналогичные построения проведем для неравенства  6·Vа + 7·Vв ≤ 4200

(Vа=700, Vв=0) и (Vа=0, Vв=600)  прямая (2).

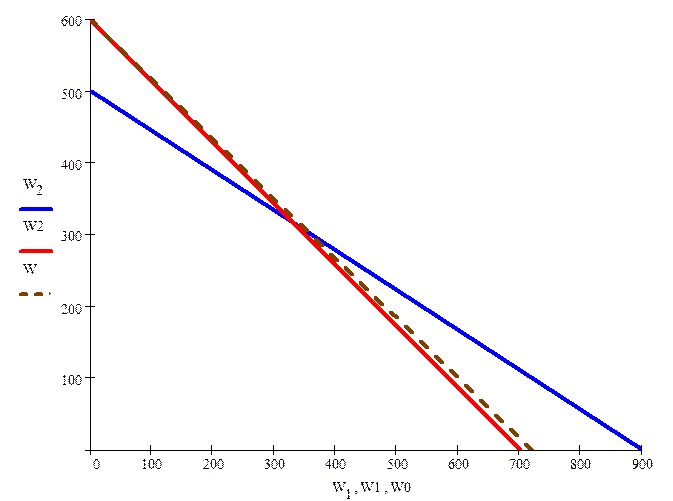
Рис. 1.

Граничные условия соответствуют двум дополнительных неравенствам, которые определяют не отрицательность переменных Vа и Vв.

Координаты всех точек многоугольника ABCO имеют такие значения Vа и Vв, которые удовлетворяют системе неравенств (1.1) - (1.2) и образуют область допустимых решений.

Построение  графика целевой функции.

Для графического представления целевой функции зададимся произвольным значением F=378000 и построим линию (3), которая называется линией уровня целевой функции (рис. 1):

F = 500×Vа + 600×Vв = 360000                           

по точкам (Vа=0,Vв=600) и (Vа=720, Vв=0)

Возможное увеличение целевой функции связано с удалением прямой от начало координат. Стрелка на рис. 1. указывает направление возрастания F. Максимума она достигает в вершине B многоугольника ABCO.

Таким образом, получено решение: оптимальный план производства проката, при котором обеспечивается максимальный доход от его реализации

Vа = 320 т. и Vв =320 т.  F = 352000 у.е.

На основании рассмотренного примера можно сделать вывод: оптимальным  решением всегда являются координаты вершины области допустимых решений.

Применение симплекс-метода для решения задач линейного программирования.

В стандартной  форме целевая функция должна быть минимизирована, а ограничения представлены в виде равенств с  неотрицательными переменными. Исходя из этих правил, можно представить стандартную форму записи математической модели задачи рационального  распределения  ресурсов, рассмотренной выше:

F' = - 500×Vа - 600×Vв à min

5×Vа + 9×Vв + V1 = 4500

6×Vа + 7×Vв + V2 = 4200

где V1,V2 - в данном случае определяют разницу между располагаемым и потребляемым ресурсами, т.е. запас ресурса.

При выполнении курсовой работы подробнее остановимся на табличной реализации симплекс-метода, поскольку табличный способ реализации симплекс-метода предполагает выполнение ряда однотипных операций, связанных с преобразованием таблиц специального вида. Эти действия легко алгоритмизуются и используются как основа в комплексах программ на ЭВМ.

На первом этапе необходимо преобразовать математическую  модель, таким образом, чтобы выразить базисные переменные через свободные. Поскольку в опорном решении базисные переменные соответствуют V1, V2, а свободные Vа = 0, Vв = 0, то система примет вид:

V1  =  4500   -  (5×Vа + 9×Vв)

V2  =     4200   -  (6×Vа + 7×Vв)                  

F'  =      0    -  (500×Vа + 600×Vв)

Аналогичное представление будет соответствовать каждому шагу табличного симплекс-метода и достаточно наглядно его можно представить с помощью симплекс-таблицы,  структура которой может быть различной. Будем использовать следующий вид таблицы.

Шаг первый:

Целевая функ-	Свободные члены	Свободные переменные
ция, базис	уравнений	-Vа	-Vв
F`	0 4500×(-66)=-297000	500 5×(-66)=-330	600×(-l) 600×(-0,11)=-66
V1	4500×l  495	5×l 0,55	9 l=1/9=0.11
V2	4200 4500×(-0,77)=-3465	6 5×(-0,77)=-3,85	7×(-l) 7×(-0,11)=-0,77

Шаг второй:

Целевая функ-	Свободные члены	Свободные переменные
ция, базис	уравнений	-V1	-Vв
F`	-297000 735×(-78)=-57330	170(-l) 170(-l)=-78	-66 -0,77×(-78)=60
Vа	495 735×(-0,25)=-184	0,55(-l)                0,55(-l)= -0,25	0.11  -0,77(-0,25)=0,19
V2	735×l 735×l=338	2,15 l=1/2,15=0.46	-0,77×l  -0,77×l= -0,35

Шаг третий:

Целевая функ-	Свободные члены	Свободные переменные
ция, базис	уравнений	-V1	-V2
F`	-350330	-78(-l)         -78(-l)=169	-6
Vа	311	-0,25(-l) -0,25(-l) =0,542	0,3
Vв	338×l 338×l=734	0.46     l=1/0,46=2,17	-0,35×l -0,35×l=-0,76

Полученное решение (столбец свободных членов) является допустимым и оптимальным, исходя из представленных выше правил анализа симплекс-таблиц.

Отсюда оптимальное  решение,  соответствующее  min F ' (max F) имеет вид:  Va = 311 т - объём проката А;

Vв = 338 т  – объём проката В.

Максимальная стоимость  отпущенной  электроэнергии F = 350330 тыс.рублей, что полностью совпадает с  решением полученным графическим способом.

2.Задача 3

Линейного программирования (количество переменных n = 4)

Задача №3: Районная энергосистема включает в себя 4 ТЭС. В качестве топлива на ТЭС могут использоваться бурый уголь, каменный уголь, газ, мазут. Известны запасы каждого вида топлива и удельный расход топлива