























Первым этапом проектирования САУ является выбор по заданным характеристикам входных сигналов и помех структурной схемы (передаточной функции), обеспечивающей в некотором смысле наилучшую (оптимальную) характеристику системы. Очевидно, что передаточная функция оптимальной системы будет зависеть не только от характеристик входного сигнала и помех, но и от выбранного критерия оптимальности. Во многих следящих системах критерием оптимальности является минимум среднего квадрата ошибки.
Если структура (передаточная функция) системы задана, а неизвестны только её оптимальные параметры, то возникает задача параметрической оптимизации. Так как структура системы известна, то можно найти выражение для среднего квадрата ошибки как функцию параметров системы:
εc2 =εc2(α1,α2,...,αn ), (7.1)
где αi – параметры системы. Для расчёта оптимальных значений αi надо найти минимум εc2.
Другой способ оптимизации заключается в моделировании исследуемой системы и подборе её параметров.
Как известно [1-3], средний квадрат суммарной ошибки εc2 состоит из двух слагаемых
εc2 = ε2уст + σξ2, (7.2)
Первое слагаемое εуст2 – квадрат динамической ошибки, второе слагаемое σξ2 обусловлено действием входной помехи n( )t . Если помеха отсутствует, то средний квадрат суммарной ошибки будет равен квадрату динамической ошибки. В случае отсутствия полезного сигнала εc2 будет определяться только помехой.
Задание к лабораторной работе
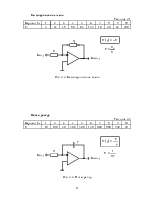
В качестве исследуемого объекта примем интегратор
с передаточной функцией H( )p = K![]() p, охваченный отрицательной обратной связью
p, охваченный отрицательной обратной связью
(рис.7.1).
Определить оптимальное значение коэффициента передачи системы
K , минимизирующее средний квадрат суммарной ошибки. Известно [1-3], что с увеличением K динамическая ошибка εуст2 уменьшается, а σξ2 растет. Следовательно, существует оптимальное значение Kопт , при котором средний квадрат суммарной ошибки будет минимальным.
Порядок выполнения работы
Структурная схема параметрической оптимизации приведена на рис.7.1. Входной сигнал представляет собой сумму полезного линейноизменяющегося сигнала g( )t = vt и помехи n( )t .
Измеритель среднего квадрата суммарной ошибки выполняет следующую операцию:
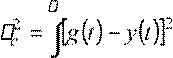 dt , (7.3) где τ
- время анализа. В работе
dt , (7.3) где τ
- время анализа. В работе ![]() c.
c.
n( )t
g( )t 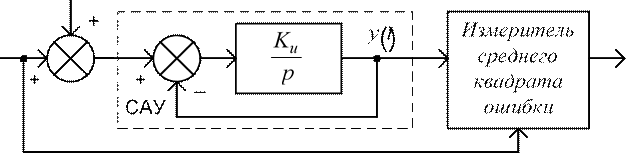 εc2
εc2
Рис. 7.1. Структурная схема параметрической оптимизации
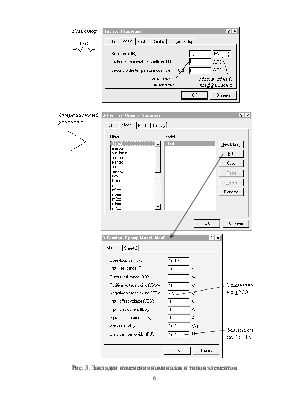
Загрузить исследуемую схему из файла Lab_7.ewb (рис.7.2). Уяснить назначение каждого элемента в схеме. Провести предварительное исследование действующих в схеме сигналов с целью изучения ее работы.
С помощью сумматора S1 (рис.1.2) можно изменить уровень сигнала, подаваемого на соответствующий вход.
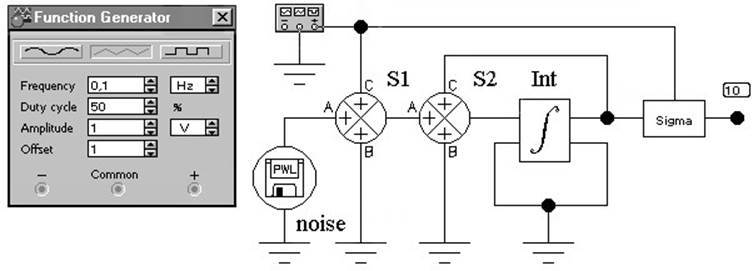
Рис. 7.2. Исследуемая схема
Произвести параметрический анализ схемы (Analysis/ Parameter Sweep, см. рис.6) при отсутствии помехи n( )t . Коэффициент усиления K интегратора следует менять от 10 до 40 с шагом 5. Измерить все значения дисперсии ошибки εc2 в момент времени, равный 1c. Построить зависимость εc2( )K .
Отключить сигнал, а на вход подать помеху n( )t . Построить зависимость εc2( )K .
Включить сигнал и помеху. Построить зависимость εc2( )K для различных уровнях помехи (значения коэффициента передачи сумматора по входу A, взять равными .60 , 1.0 и 1.5).
Для каждой зависимости найти значение Ko, соответствующее минимуму среднего квадрата ошибки.
Содержание отчёта
Отчёт по лабораторной работе должен содержать:
− структурную схему оптимизируемой системы;
− описание схемы;
− графики зависимостейεc2( )K ;
− осциллограммы входного, выходного сигналов и напряжения ошибки;
− оптимальные значения коэффициента усиления K , полученные теоретически и экспериментально;
− выводы по результатам оптимизации с анализом полученных зависимостей.
Контрольные вопросы
1. В чем заключается задача оптимизации?
2. Какие критерии используются при оптимизации?
3. Что такое параметрическая оптимизация?
4. Объясните экспериментальную зависимость среднего квадрата ошибки от коэффициента усиления.
5. Как изменится оптимальное значение коэффициента усиления при увеличении интенсивности помех?
6. Как изменится оптимальное значение коэффициента усиления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.