
















Построить потенциальную диаграмму для контура, который включает оба источника ЭДС.
4)Методом
эквивалентного генератора найти ток в ветви с ЭДС ![]() .
.
5) Составить сводную таблицу результатов расчета токов ветвей, выполненных разными методами.
Параметры источников даны в таблице 1.1, а параметры резисторов - в таблице 1.2.
Таблица 1.1
|
Параметры источников |
|
|
|
|
|
|
15 |
18 |
3 |
2 |
4 |
Таблица 1.2
|
Сопротивления резисторов, Ом |
|
|
|
|
|
|
|
|
6 |
4 |
9 |
5 |
7 |
4 |
5 |
Исходная схема на рисунке 1
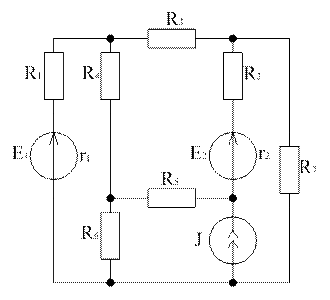
Рисунок 1
Решение:
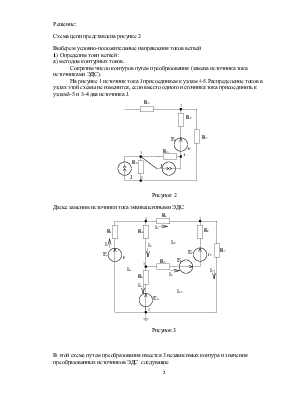
Схема цепи представлена рисунке 2
Выберем условно-положительные направления токов ветвей
1) Определим токи ветвей : а) методом контурных токов.
Сократим число контуров путем преобразования (замена источника тока источниками ЭДС).
На рисунке 1 источник тока J присоединяем к узлам 4-5.Распределение токов в узлах этой схемы не изменится, если вместо одного источника тока присоединить к узлам3-5 и 3-4 два источника J.
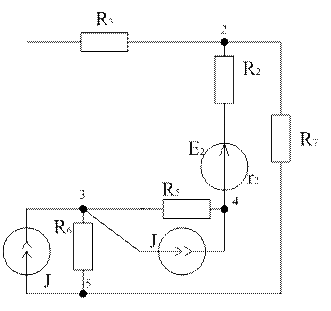
Рисунок 2
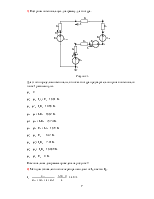
Далее заменим источники тока эквивалентными ЭДС.
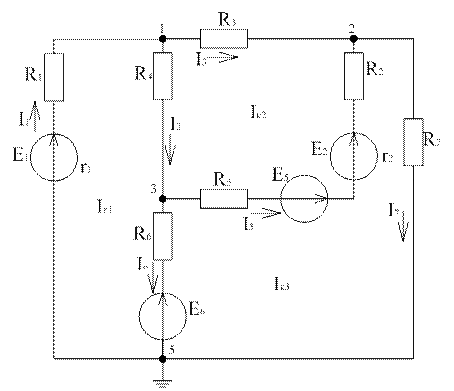
Рисунок 3
В этой схеме путем преобразования имеется 3 независимых контура и значения преобразованных источников ЭДС следующие
![]() В
В
![]() В
В
Составим систему уравнений по методу контурных токов:
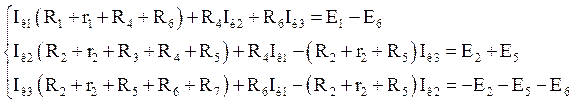
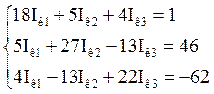
Решим систему уравнений методом Крамера
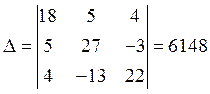
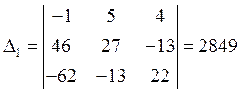
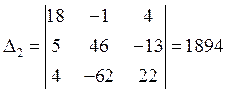
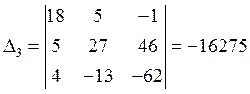
Отсюда получим:
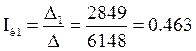 А
А
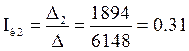 А
А
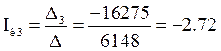 А
А
На основании выбранных направлений токов в ветвях и направлений контурных токов получим:
![]() А
А
![]() А
А
![]() А (истинное направление противоположно заданному)
А (истинное направление противоположно заданному)
![]() А
А
![]() А (истинное направление противоположно заданному)
А (истинное направление противоположно заданному)
![]() А
А
б) методом узловых потенциалов.
Примем потенциал узла 5 равным нулю (![]() ).
В схеме 3 узла потенциалы, которых нужно определить.
).
В схеме 3 узла потенциалы, которых нужно определить.
Для узла 1:
Собственная проводимость
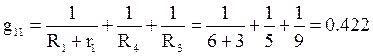 См.
См.
Взаимная проводимость
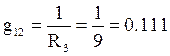 См
См
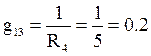 См
См
Для узла 2:
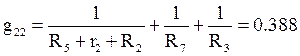 См.
См.
![]() См
См
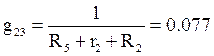 См.
См.
Для узла 3:
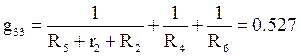 См.
См.
![]() См.
См.
![]() См.
См.
Составим уравнения
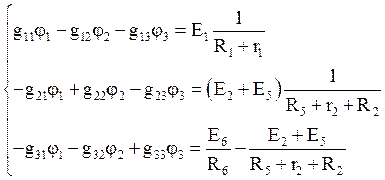
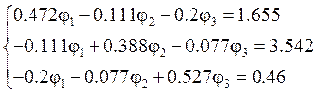
В
матричном виде систему уравнений можно записать в виде ![]() , где матрица проводимостей
G
, где матрица проводимостей
G
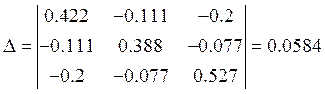
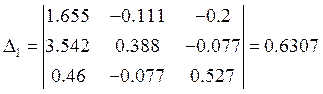
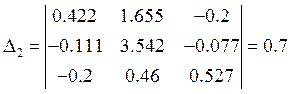
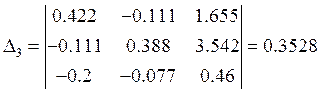
Отсюда получим:
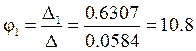 В
В
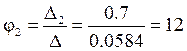 В
В
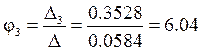 В
В
Определим токи:
1)Ток ![]() ;
;
![]() В.
В. ![]() В. Отсюда
В. Отсюда
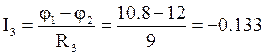 А.
А.
(истинное направление противоположно заданному)
2)
Ток ![]() ;
;
![]() В.
В.
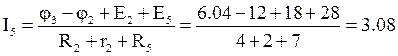 А.
А.
3)
Ток ![]() ;
;
![]() В. Отсюда
В. Отсюда
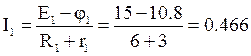 В. Отсюда
В. Отсюда
4)
Ток ![]() ;
;
![]() В. Отсюда
В. Отсюда
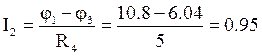 А.
А.
5) Ток ![]() ;
;
![]() В. Отсюда
В. Отсюда
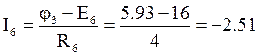 А.
А.
(истинное направление противоположно заданному)
6) Ток ![]() ;
;
![]() В. Отсюда
В. Отсюда
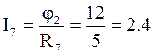 А.
А.
2) Составим
баланс мощностей (по результатам расчета методом контурных токов ЭДС ![]() являются
генераторами, а
являются
генераторами, а ![]() является
потребителем)
является
потребителем)
![]()
![]() Вт
Вт
![]()
![]() Вт
Вт
Определим погрешность расчета:
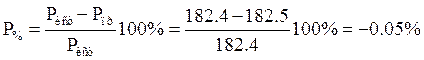
Допускается погрешность 3%
Так как ![]() ,
то баланс мощностей выполняется.
,
то баланс мощностей выполняется.
3) Построим потенциальную диаграмму для контура.
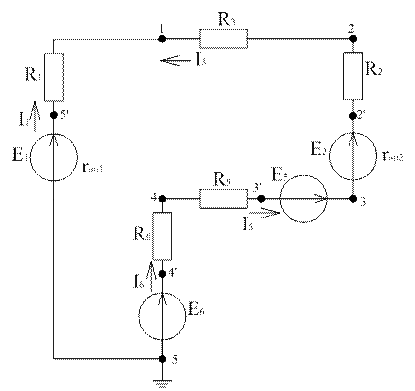
Рисунок 4
Для этого определим потенциалы, в точках контура предварительно приняв потенциал в точке 1 равным нулю.
![]()
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
Потенциальная диаграмма приведена на рисунке 9
4) Методом эквивалентного генератора находим ток ![]() в
ветви
в
ветви ![]() .
.
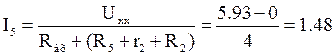 А.
А.
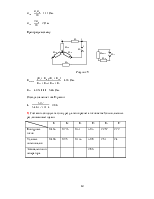
Определим потенциалы точек 2 и 3
Решим задачу методом контурных токов для 2-х контуров
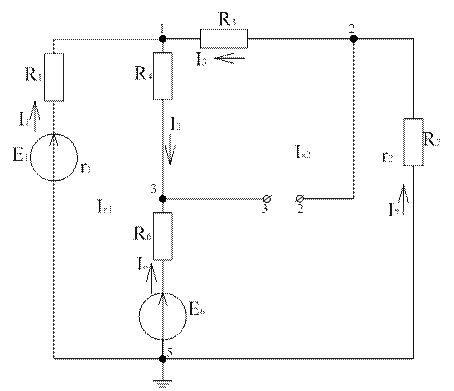
Рисунок 5
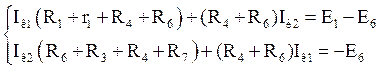
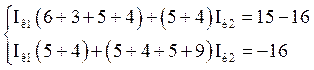
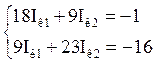
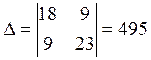
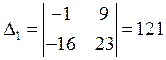
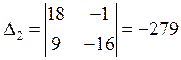
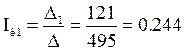 А.
А.
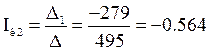 А.
А.
![]() А.
А.
![]() А.
А.
![]() А.
А.
![]() А.
А.
Примем ![]()
![]() В.
В.
![]() В.
В.
С учетом ![]() в
ветви 2-3:
в
ветви 2-3:
![]() В.
В.
![]() В.
В.
Определим входное
сопротивление ![]() .
.
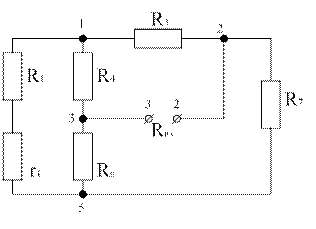
Рисунок 6
![]() Ом.
Ом.
Преобразуем
«треугольник» сопротивлений ![]() в
эквивалентную «звезду»
в
эквивалентную «звезду»
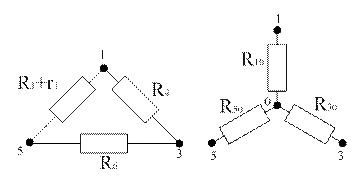
Рисунок 7
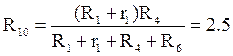 Ом.
Ом.
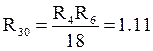 Ом.
Ом.
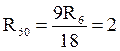 Ом.
Ом.
Преобразуем схему:
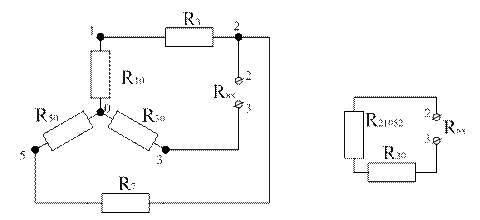
Рисунок 8
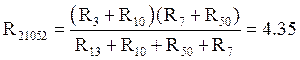 Ом.
Ом.
![]() Ом.
Ом.
Отсюда значение тока ![]() равно:
равно:
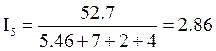
5) Составить сводную таблицу результатов расчета токов ветвей, выполненных различными методами.
|
|
|
|
|
|
|
|
|
Контурных токов |
0.463 |
0.773 |
0.31 |
3.03 |
2.257 |
2.72 |
|
Узловых потенциалов |
0.466 |
0.95 |
0.133 |
3.08 |
2.51 |
2.4 |
|
Эквивалентного генератора |
2.86 |
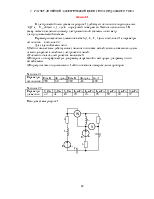
2 РАСЧЕТ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Задача 2.1
В электрической цепи (схема на
рисунке 1) действуют источники синусоидальных ЭДС ![]() , где k – порядковый номер ветви. Частота
источников- f. В схему также включены
вольтметр электромагнитной системы и ваттметр электродинамической системы.
, где k – порядковый номер ветви. Частота
источников- f. В схему также включены
вольтметр электромагнитной системы и ваттметр электродинамической системы.
Параметры пассивных элементов
ветвей (![]() )даны в таблице
2.1,а параметры источников – в таблице 2.2.
)даны в таблице
2.1,а параметры источников – в таблице 2.2.
Для заданной схемы цепи:
1)Найти комплексные действующие значения токов всех ветвей, воспользовавшись одним из методов расчета линейных электрических цепей:
2)Составить баланс электрических мощностей.
3)Построить топографическую диаграмму напряжений и векторную диаграмму токов ветвей схемы.
4)По результатам, полученным в п.1,найти показания измерительных приборов.
Таблица 2.1
|
Параметры источников |
|
|
|
|
|
|
280 |
60 |
260 |
-45 |
400 |
Таблица 2.2
|
Параметры элементов |
|
|
|
|
|
|
|
|
|
|
32 |
34 |
40 |
20 |
16 |
28 |
50 |
30 |
27 |
Исходная схема рисунок 1
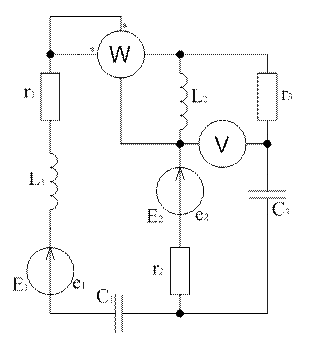
Решение
Схема представлена на рисунке 2
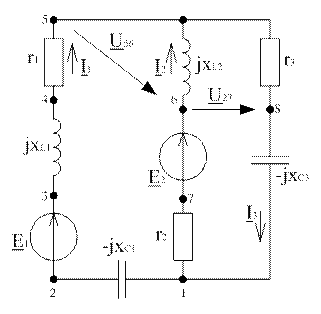
Рисунок 2
1)Определим комплексные токи ветвей
Определим сопротивления реактивных элементов цепи:
![]() Ом
Ом
![]() Ом
Ом
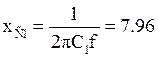 Ом
Ом
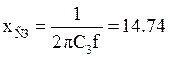 Ом
Ом
Действующие значения напряжений
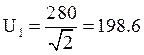 В
В 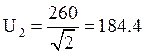 В
В
Выразим напряжения и сопротивления в комплексной форме:
![]() Ом
Ом
![]() Ом
Ом
![]() Ом°
Ом°
![]() Ом
Ом
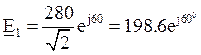 В
В 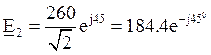 В
В
Составим систему уравнений по методу контурных токов.
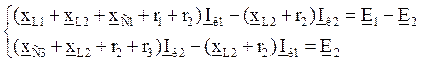
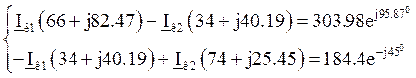
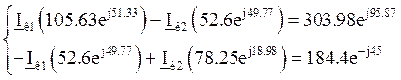
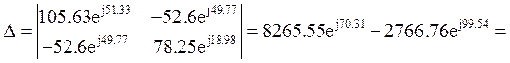
![]()
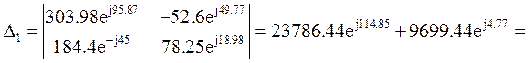
![]()
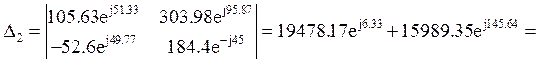
![]()
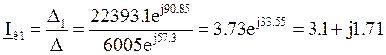 A
A
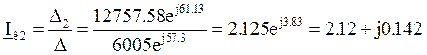 A
A
Определим токи ветвей с учетом их направлений контурных токов, показанных на рис.2.1
![]() A
A
![]() A
A
![]() A
A
2)Составим баланс активных и реактивных мощностей
![]()
![]() ВА
ВА
Активная мощность, отдаваемая
источником: ![]() Вт
Вт
Реактивная мощность,
отдаваемая источником: ![]() ВАР (мощность индуктивного характера)
ВАР (мощность индуктивного характера)
Активная мощность приемника:
![]() Вт
Вт
Реактивная мощность приемника:
![]()
![]() ВАР
ВАР
Определим погрешность расчетов
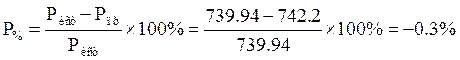
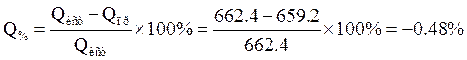
Допускается погрешность 3%. Баланс мощностей выполняется
3)Для построения топографической диаграммы напряжений необходимо определить падения напряжений на всех участках цепи
![]() В
В
![]() В
В
![]() В
В
![]() В.
В.
![]() В.
В.
![]() В.
В.
![]() В.
В.
Векторная диаграмма токов и топографическая диаграмма напряжений приведены на рисунке 2.
4) Определим показания измерительных приборов.
![]()
Тогда
![]() В.
В.
![]() В.
В.
Показания вольтметра
![]()
![]() В.
В.
Таким образом, вольтметр
покажет действующее значение напряжения: ![]() В.
В.
Определим показания ваттметра.
Обмотка напряжения ваттметра
включена на падение напряжения на индуктивности ![]()
и через токовую обмотку
ваттметра проходит ток ![]() .
.
Отсюда получаем
![]() Вт.
Вт.
Задача 2.2
К
электрической цепи приложено синусоидальное напряжение ![]() .Частота источников- f. Между ветвями цепи имеется
индуктивная связь с коэффициентом k.
.Частота источников- f. Между ветвями цепи имеется
индуктивная связь с коэффициентом k.
Параметры
пассивных элементов ветвей (![]() даны в таблице 2.1,а параметры
источников – в таблице 2.2.
даны в таблице 2.1,а параметры
источников – в таблице 2.2.
Для заданной схемы цепи:
1)Найти комплексные действующие значения токов всех ветвей.
2)Составить баланс электрических мощностей для исходной схемы.
3)Построить топографическую диаграмму напряжений и векторную диаграмму токов ветвей исходной схемы.
Параметры синусоидального источника приведены в таблице 2.3, а параметры пассивных элементов схемы – в таблице 2.4.
Таблица 2.3
|
Параметры источников |
|
|
|
|
280 |
60 |
f, Гц |
Таблица 2.4
|
Параметры элементов |
|
|
|
|
|
|
|
k |
|
32 |
34 |
40 |
20 |
16 |
28 |
50 |
0,55 |
Исходная схема рисунок 1
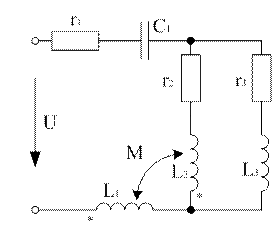
Решение
Схема представлена на рисунке 2
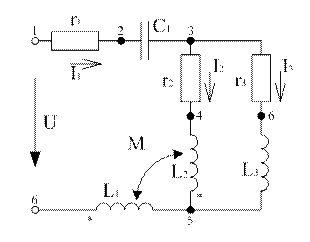
Рисунок 2
Составим уравнения по законам Кирхгофа для мгновенных значений токов и напряжений.
1) Определим сопротивления реактивных элементов цепи:
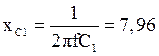 Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
Сопротивление взаимной индукции
![]() Ом
Ом
Определим комплексные сопротивления ветвей
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
Для определения действующих значений токов ветвей применим правило индуктивной развязки и получим эквивалентную схему без индуктивной связи. Так как индуктивно связанное катушки присоединены к одному узлу
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.