Метод Монте-Карло. Численный метод определения вероятностных закономерностей случайных явлений, страница 3

Найдем решение этой же задачи методом Монте-Карло. С помощью генератора (см. рисунок 2.12) получим последовательность 10 тыс. случайных чисел, подчиняющихся экспоненциальному (показательному) распределению с параметрами l₁=5∙10^–7 (рисунок 2.20), l₂=4∙10^–7 и l₃=5∙10^–7 (рисунок 2.21), моделирующих время безотказной работы первого, второго и третьего элементов, соответственно.

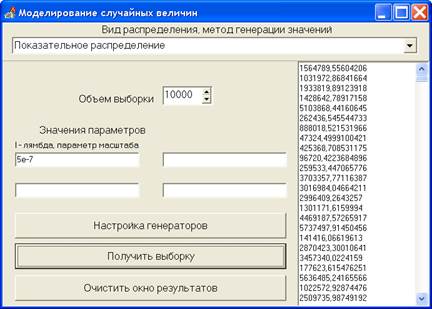
Рисунок 2.20 – Моделирование 10 тысяч реализаций логнормально распределенной случайной величины в программе «ModelSV»

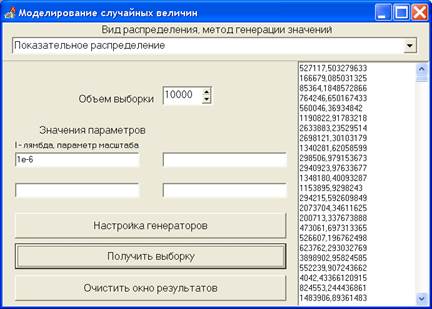
Рисунок 2.21 – Моделирование 10 тысяч реализаций логнормально распределенной случайной величины в программе «ModelSV»

В колонке «E» (рисунок 2.22) определим время безотказной работы системы в каждом из 10 тыс. «испытаний». Причем, в соответствии со структурной схемой надежности (см. рисунок 2.19) время безотказной работы системы определяется максимальной наработкой двух параллельно соединенных элементов («1» и «2») и минимальной наработкой двух последовательно соединенных подсистем (подсистемы элементов «1»–«2» и элемента «3»). На рисунке 2.22 отображается соответствующая формула.

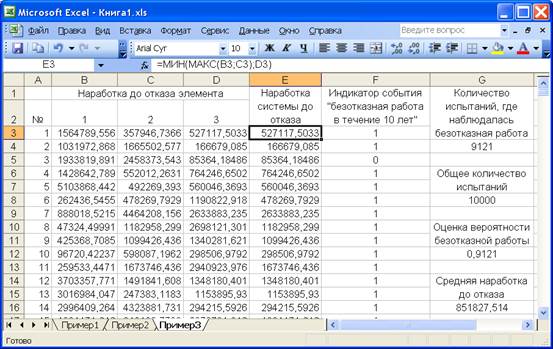
Рисунок 2.22 – Моделирование 10 тысяч реализаций логнормально распределенной случайной величины в программе «ModelSV»

В колонке «F» определим значения индикатора события «безотказная работа подводного перехода нефтепровода в течение 10 лет (87600 часов)» (на рисунке 2.22 отображается соответствующая формула). Единица в ячейках колонки «F» указывает на то, что в очередном «испытании» время безотказной работы системы превысило 87600 часов, иначе в ячейках колонки «F» стоит ноль.

Подсчитывается количество единиц в колонке «F» (см. ячейку «G4» на рисунке 2.22), определяющее количество «испытаний», в которых имела место безотказная работа подводного перехода нефтепровода в течение 10 лет. Вероятность данного события оценивается как отношение количества «успешных испытаний» (ячейка «G4»), к общему количеству «испытаний» (см. ячейку «G12» на рисунке 2.22). Среднее время безотказной работы подводного перехода нефтепровода оценивается как среднее арифметическое значение результатов 10 тыс. «испытаний» (см. ячейку «G16»).

Полученные методом Монте-Карло значения вероятности безотказной работы подводного перехода нефтепровода в течение 10 лет (0,9121) и среднего времени безотказной работы (851827,5 часов) незначительно отличаются от точных аналитических значений соответствующих показателей безотказности, полученных ранее в пакете MathCAD (0,915; 8,55∙10⁵ часов).