Метод Монте-Карло (метод статистических испытаний) – численный метод определения вероятностных закономерностей случайных явлений, основанный на получении большого количества реализаций случайной величины (с использованием, как правило, программного генератора случайных чисел), обладающей с изучаемым явлением тождественными вероятностными характеристиками.
Пример 1. Рассмотрим пример использования метода Монте-Карло для определения вероятности безотказной работы пальца гусеницы трактора, если предполагается, что нагрузка, прикладываемая к пальцу, подчиняется логнормальному распределению с математическим ожиданием 20 МПа и стандартным отклонением 10 МПа, а предел прочности пальца составляет 40 МПа. Отказ объекта происходит при превышении нагрузкой предела прочности.
С помощью одного из существующих генераторов (рисунок 2.12) получим последовательность 10 тыс. случайных чисел, подчиняющихся логнормальному распределению с математическим ожиданием 20 МПа и стандартным отклонением 10 МПа, моделирующую значения нагрузки на палец гусеницы трактора.

Рисунок 2.12 – Программный генератор случайных величин «ModelSV», доступный на сайте www.shevchenkodn.narod.ru
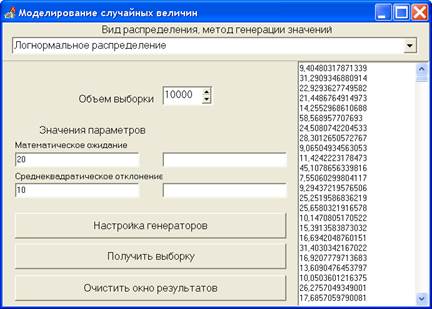
Рисунок 2.13 – Моделирование 10 тысяч реализаций логнормально распределенной случайной величины в программе «ModelSV»
Полученную случайную числовую последовательность скопируем в колонку «B» пакета MS Excel. В колонке «C» определим значения индикатора события «безотказная работа пальца гусеницы», тождественного событию «нагрузка на палец гусеницы не превышает предела прочности 40 МПа» (на рисунке 2.14 отображается соответствующая формула). Единица в ячейках колонки «C» указывает на то, что в очередном «испытании» нагрузка не превысила 40 МПа, иначе в ячейках колонки «C» стоит ноль.
![]()
![]()
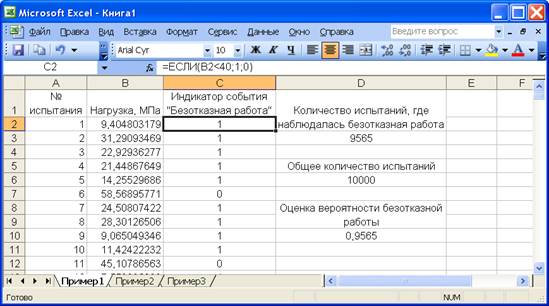
Рисунок 2.14 – Моделирование 10 тысяч реализаций «нагрузка-прочность» в пакете MS Excel
Подсчитывается количество единиц в колонке «C» (см. ячейку «D3» на рисунке 2.14), определяющее количество «испытаний», в которых имела место безотказная работа пальца гусеницы. Вероятность безотказной работы оценивается как отношение количества «успешных испытаний» (ячейка «D3»), к общему количеству «испытаний» (см. ячейку «D10» на рисунке 2.14).
Полученное методом Монте-Карло значение вероятности безотказной работы пальца гусеницы 0,9565 является приближенным[*]. Однако его точность увеличивается с увеличением количества статистических испытаний.
Пример 2. Рассмотрим пример определения вероятности безотказной работы оси мобильной машины, предполагая, что нагрузка на ось подчиняется гамма-распределению с математическим ожиданием 20 МПа и стандартным отклонением 6 МПа, а предел прочности оси мобильной машины подчиняется нормальному закону распределения с математическим ожиданием 40 МПа и стандартным отклонением 5 МПа.
Определим значения параметров a и b гамма-распределения (__см. приложение с распределениями, числовые характеристики гамма-распределения) решением системы уравнений:
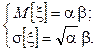
в пакете MathCAD.
Задание математических ожиданий и стандартных отклонений величины нагрузки (Mn, sn) на ось мобильной машины
![]()
![]()
Определение параметров a и b функции гамма-распределения величины нагрузки решением системы уравнений
![]()
![]()
![]()
![]()
![]()
![]()
Система уравнений решена, параметры a и b определены
![]()
![]()
С помощью генератора (см. рисунок 2.12) получим последовательность 10 тыс. случайных чисел, подчиняющихся гамма-распределению с параметрами a=11,11111 и b=1,8, моделирующую значения нагрузки на ось мобильной машины (рисунок 2.15). Затем получим аналогичное количество реализаций нормально распределенной случайной величины, моделирующей предел прочности оси мобильной машины (рисунок 2.16).

Рисунок 2.15 – Моделирование 10 тысяч реализаций гаммараспределенной случайной величины в программе «ModelSV»
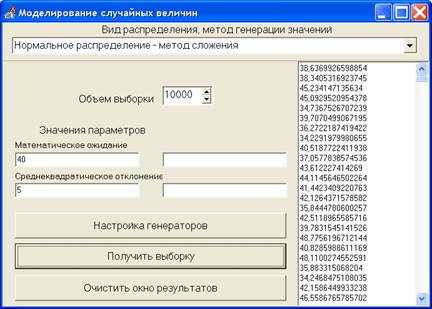
Рисунок 2.16 – Моделирование 10 тысяч реализаций нормально распределенной случайной величины в программе «ModelSV»
Полученные случайные числовые последовательности скопируем в колонки «B» и «C» пакета MS Excel (рисунок 2.17). В колонке «D» определим значения индикатора события «безотказная работа оси», когда «нагрузка на ось не превышает предела прочности» (на рисунке 2.17 отображается соответствующая формула). Единица в ячейках колонки «D» указывает на то, что в очередном «испытании» нагрузка не превысила предела прочности, иначе в ячейках колонки «D» стоит ноль.
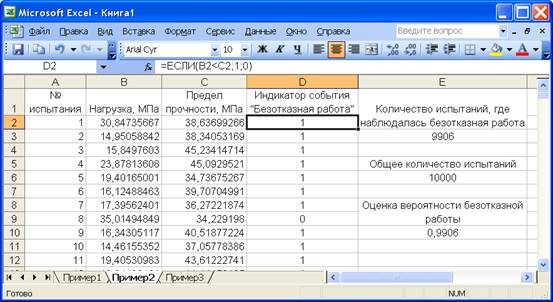
Рисунок 2.17 – Моделирование 10 тысяч реализаций логнормально распределенной случайной величины в программе «ModelSV»
Подсчитывается количество единиц в колонке «D» (см. ячейку «E3» на рисунке 2.17), определяющее количество «испытаний», в которых имела место безотказная работа оси. Вероятность безотказной работы оценивается как отношение количества «успешных испытаний» (ячейка «E3»), к общему количеству «испытаний» (см. ячейку «E10» на рисунке 2.14).
Полученное методом Монте-Карло значение вероятности безотказной работы оси мобильной машины 0,9906 незначительно отличается от точного аналитического решения 0,990466[†]. При этом точность может быть увеличена проведением дополнительных «испытаний».
Пример 3. Метод Монте-Карло можно применять и для определения показателей надежности систем. Рассмотрим пример использования метода Монте-Карло для определения показателей безотказности подводного перехода нефтепровода.
Участки нефтепровода, проходящие через водные преграды, имеют основную и резервную нитки (рисунок 2.18). Существующие правила технической эксплуатации трубопровода предусматривают штатное нагружение лишь основной нитки. При этом предполагается, что резервная нить находится в ненагруженном резерве.

Рисунок 2.18 – Технологическая схема подводного перехода нефтепровода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.