Апериодическое звено
(инерционное) - это звено, в котором связь между выходной и
входной величинами описывается следующим образом: 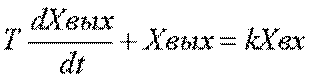 ; решение уравнения дает
математическое описание переходного процесса:
; решение уравнения дает
математическое описание переходного процесса: 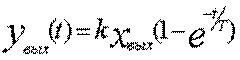 , где Т-постоянная времени (сек); K
-коэффициент усиления (передача) звена. Передаточная функция имеет вид:
, где Т-постоянная времени (сек); K
-коэффициент усиления (передача) звена. Передаточная функция имеет вид: 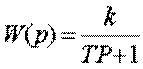 .
.
Апериодическое звено, называется также, статическим звеном первого порядка, так как при постоянном входном сигнале с течением времени устанавливается постоянная выходная величина. Звено называется еще инерционным, потому что в результате мгновенного изменения входного воздействия выходная величина изменяется не мгновенно, а с переменной скоростью, которая постепенно уменьшается до нуля.
Переходная функция ![]() (рис.- 3.13а); частотная
характеристика – АФЧХ-
(рис.- 3.13а); частотная
характеристика – АФЧХ-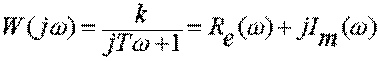 , где
, где 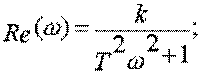 (рис.- 3.13б), АЧХ -
(рис.- 3.13б), АЧХ - 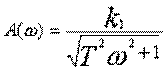 (рис.- 3.13в);
ФЧХ j=-arctgTw (рис.- 3.13г)
(рис.- 3.13в);
ФЧХ j=-arctgTw (рис.- 3.13г) 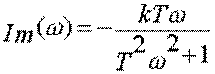 .
.
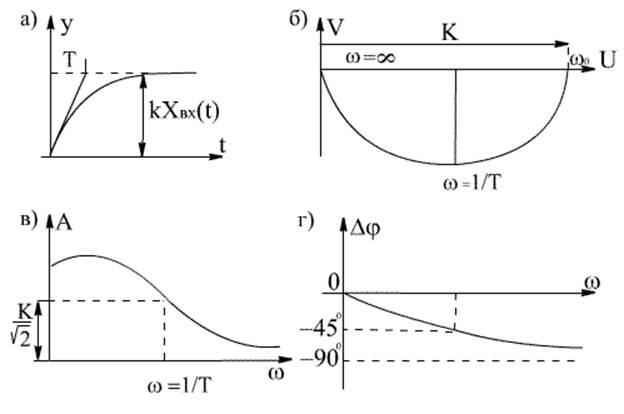 Рис. 3.13 Характеристики апериодического звена а) Переходная функция; б) АФЧХ;
в) АЧХ; г) ФЧХ
Рис. 3.13 Характеристики апериодического звена а) Переходная функция; б) АФЧХ;
в) АЧХ; г) ФЧХ
Примером апериодического звена может служить LR или RC - цепочка, магнитный усилитель, термопара, электродвигатель и т.д.
Колебательное звено. Это звено состоит из тех элементов которые обладают свойствами емкости и способом взаимно обмениваться веществами (или энергией) через сопротивления. В колебательном звене соотношение между выходной и входной величинами описывается линейным дифференциальным уравнением второго порядка при коэффициент затухания z<1:
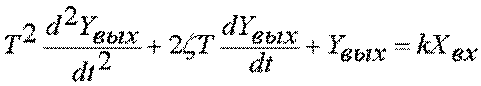 .
.
На основании этой формулы получаем, передаточную функцию
колебательного звена 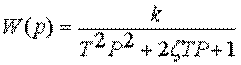 или
или 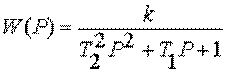 при Т1 <2T2. Т=Т2; z=
при Т1 <2T2. Т=Т2; z= ![]() ; 0 <z<1 коэффициент затухания. При z<1 процесс является затухающим колебательным
процессом, а при z>1 процессом с расходящимися колебаниями.
Частотная передаточная функция
; 0 <z<1 коэффициент затухания. При z<1 процесс является затухающим колебательным
процессом, а при z>1 процессом с расходящимися колебаниями.
Частотная передаточная функция 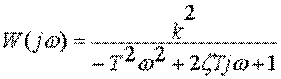 .
.
Вещественную и мнимую частотные функции (АФЧХ) определяют по формулам:
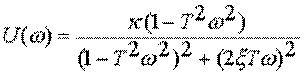 и
и
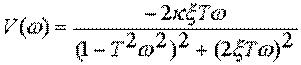 .
.
АЧХ – 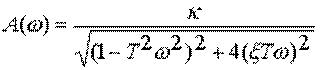
ФЧХ - 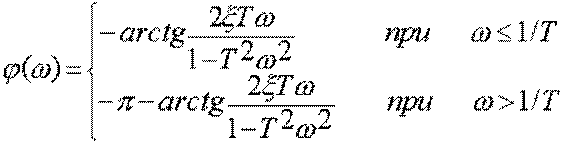
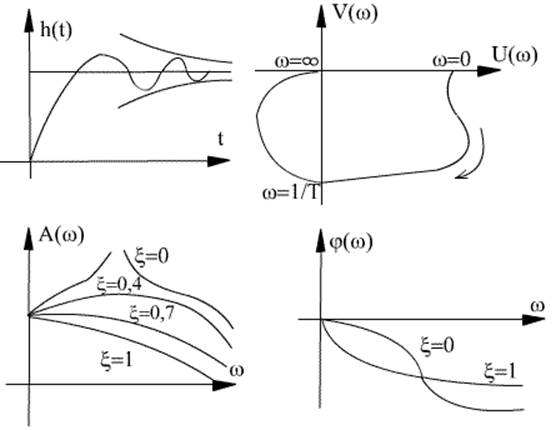 Рис. 3.14 Характеристики колебательного звена: а) Переходная функция; б) АФЧХ;
в) АЧХ; г) ФЧХ
Рис. 3.14 Характеристики колебательного звена: а) Переходная функция; б) АФЧХ;
в) АЧХ; г) ФЧХ
При Т1 >2Т2, z=1 звено называется инерционным звеном
второго порядка или статическим звеном второго порядка.
Дифференциальное уравнение инерционного (апериодического) звена второго порядка
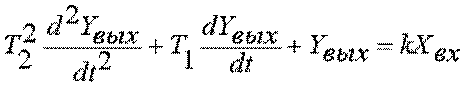 . Переда
. Переда 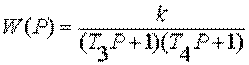 точная функция
инерценного (апериодического) звена второго порядка
точная функция
инерценного (апериодического) звена второго порядка 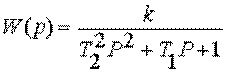 при Т1 ³ 2T2 или , здесь
при Т1 ³ 2T2 или , здесь 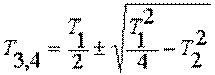 .
.
Частотная передаточная функция 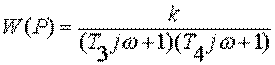 .
.
АЧХ- 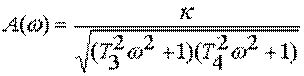 ;
;
ФЧХ - ![]() .
.
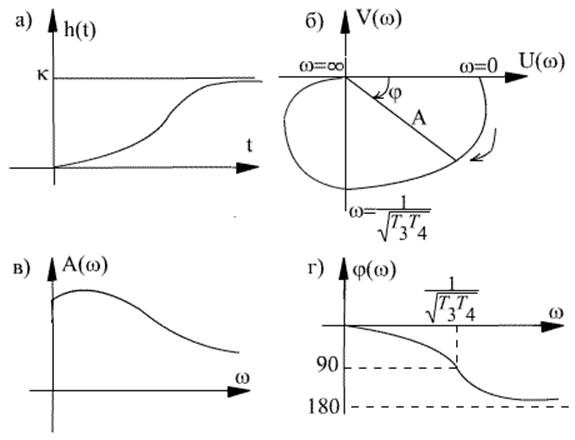 Рис. 3.15 Характеристики инерционного (апериодического) звена второго порядка
а) Переходная функция; б) АФЧХ; в) АЧХ; г) ФЧХ
Рис. 3.15 Характеристики инерционного (апериодического) звена второго порядка
а) Переходная функция; б) АФЧХ; в) АЧХ; г) ФЧХ
Примерами колебательного звена может служить электродвигатель постоянного тока независимого возбуждения, включаемый в холостую, в котором входной величиной является напряжение, а выходной – скорость вращения вала; RLС электрическая цепь, мембранный исполнительный механизм, поплавковый дифманометр.
Интегрирующее звено (астатическое звено первого
порядка). Интегрирующим называют звено, которе описывается уравнением 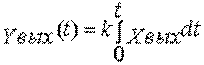 или
или 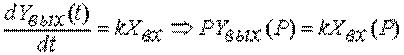 , откуда
получаем передаточную функцию интегрирующего звена
, откуда
получаем передаточную функцию интегрирующего звена 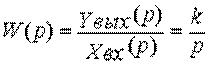 . В интегрирующем звене скорость
выходного сигнала пропорциональна входному сигналу. Такое звено называется
также астатическим звеном первого порядка.
. В интегрирующем звене скорость
выходного сигнала пропорциональна входному сигналу. Такое звено называется
также астатическим звеном первого порядка.
При постоянном значении входного воздействия Yвых(t)=kXвх(t) и при единичном скачке на входе звена выходная величина интег-рирующего звена пропорциональна времени Yвых(t)=h(t)=kt (рис. 3.16а).
Частотная передаточная функция 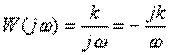 , остальные частотные функции имеют
следующий вид: U(w)=0; V(w)=-
, остальные частотные функции имеют
следующий вид: U(w)=0; V(w)=- ![]() ; A(w)=
; A(w)= ![]() ; w(j)= -90o (рис. 3.16 б,в,г).
; w(j)= -90o (рис. 3.16 б,в,г).
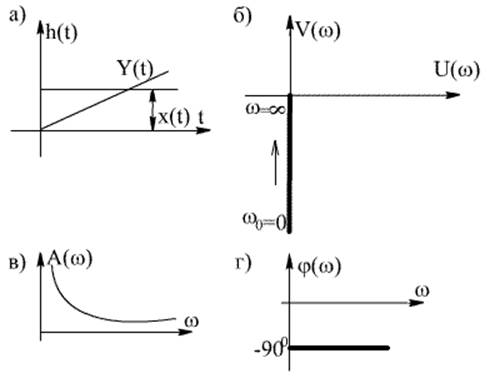 Рис. 3.16 Характеристики и нтегрирующего звена
а) Переходная функция; б) АФЧХ; в) АЧХ; г) ФЧХ
Рис. 3.16 Характеристики и нтегрирующего звена
а) Переходная функция; б) АФЧХ; в) АЧХ; г) ФЧХ
Примером интегрирующего звена могут служить гидравлические двигатели, n=f(U), электрический индукционный счетчик и др.
Интегрирующие звенья придают САР астатический характер. Поэтому они могут вводиться в исходную САР как корректирующие устройства, повышающие точность регулирования.
Дифференцирующее звено. Различают идеальное и
реальное дифференциальное звено. Идеальным дифференцирующим звеном является
динамическое типовое звено САР, математическое описание которого приводится к
виду Yвых(t)=t 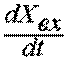 или
или 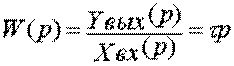 , где t- постоянная времени звена. Частотная
передаточная функция
, где t- постоянная времени звена. Частотная
передаточная функция ![]() , остальные частотные функции имеют
следующий вид: U(w)=0; V(w)=tw; A(w)=tw; w(j)= 90o (рис. 3.17). При подаче на вход
идеального дифференцирующего звена единичного воздействия, выходная величина
совершает скачок в бесконечность, что соответствует бесконечно большой скорости
нарастания входной величины (рис.-3.17а). Выходная величина идеального
дифференцирующего звена пропорциональна скорости изменения входной величины и
при изменении входной величины переходный процесс должен происходить мгновенно.
Такое звено можно представить в виде электрической цепи, где выходное
сопротивление равно нулю.
, остальные частотные функции имеют
следующий вид: U(w)=0; V(w)=tw; A(w)=tw; w(j)= 90o (рис. 3.17). При подаче на вход
идеального дифференцирующего звена единичного воздействия, выходная величина
совершает скачок в бесконечность, что соответствует бесконечно большой скорости
нарастания входной величины (рис.-3.17а). Выходная величина идеального
дифференцирующего звена пропорциональна скорости изменения входной величины и
при изменении входной величины переходный процесс должен происходить мгновенно.
Такое звено можно представить в виде электрической цепи, где выходное
сопротивление равно нулю.
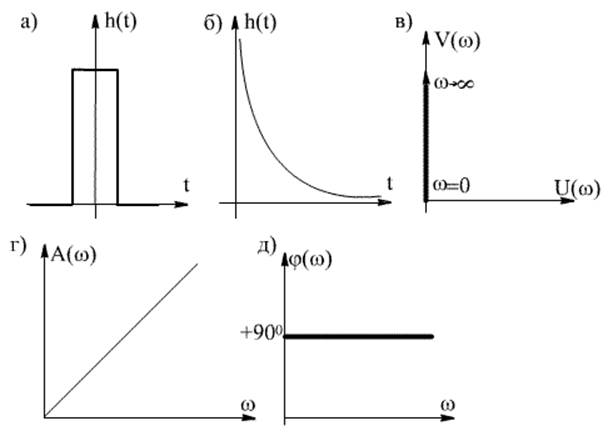 Рис. 3.17 Характеристики дифференцирующего звена
а) и б) Переходная функция; в) АФЧХ; г) АЧХ; д) ФЧХ
Рис. 3.17 Характеристики дифференцирующего звена
а) и б) Переходная функция; в) АФЧХ; г) АЧХ; д) ФЧХ
Реальным дефференцирующим звеном первого порядка называют
динамическое типовое звено САР, математическое описание которого приводится к
виду Yвых(t)=k(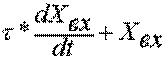 ) или
) или 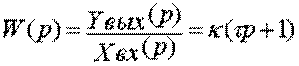 . Переходный процесс в реальном
дифференцирующем звене представлен на рис. 3.17б. Примером дифференцирующего
звена служить тахогенератор, операционный
. Переходный процесс в реальном
дифференцирующем звене представлен на рис. 3.17б. Примером дифференцирующего
звена служить тахогенератор, операционный
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.