Прочностной расчёт основных элементов. Расчёт первой цилиндрической передачи поворотного редуктора. Закрытая нереверсивная цилиндрическая прямозубая передача

2.4. Прочностной расчёт основных элементов

2.4.1. Расчёт первой цилиндрической передачи поворотного редуктора.

Закрытая нереверсивная цилиндрическая прямозубая передача, предназначена для трёхсменной работы в течение одного года. Материал шестерни сталь 20ХН3А(цементация, закалка, низкий отпуск) твёрдостью  НRC 56...63, материал колеса сталь 20ХН3A(цементация, закалка, низкий отпуск) твёрдостью НRC 56...63. Передаваемая мощность  кВт; коэффициент ширины колеса ; частота вращения шестерни , колеса .

Пределы контактной выносливости для шестерни и колеса[2.c.146.]

 МПа;                (2.31)

              МПа;                (2.32)

        Допускаемые контактные напряжения для шестерни и колеса[2.c.146.]

                                    ,                               (2.33)

где - коэффициент безопасности для колёс, прошедших улучшение и нормализацию[2.c.146.], ;

-коэффициент долговечности[2.c.146.], =1;

для шестерни

 МПа;

для колеса

 МПа.

Допускаемые напряжения при изгибе колеса и шестерни при расчете на усталость

МПа,                        (2.34)

где - предел выносливости зубьев по напряжением изгиба [2.с.147],

- коэффициент безопасности,

Допускаемые напряжения при изгибе

Определение основных параметров передачи.

Межосевое расстояние передачи [2.c.115]

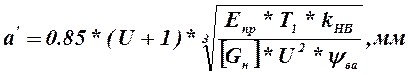,             (2.35)

где -приведенный модуль упругости материала колеса;

- коэффициент ширины колеса относительно межосевого расстояния[2.c.117];

- коэффициент неравномерности распределения нагрузки по длине зуба[2.c.111];

- вращающий момент на колесе.

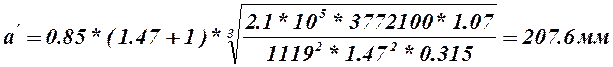
Принимаем

Ширина колеса  

Принимаем .

Диаметры начальных  окружностей колеса

,            (2.36)

                 (2.37)

Задаем число зубьев шестерни

.

Число зубьев колеса

.,                        (2.38)

Нормальный модуль

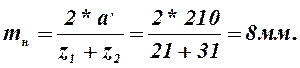,                        (2.39)

Проверка передачи по контактным напряжениям.

Условие прочности имеет вид[2.c.144]

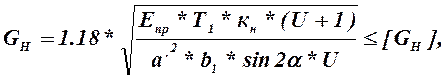,                    (2.40)

где - коэффициент нагрузки.

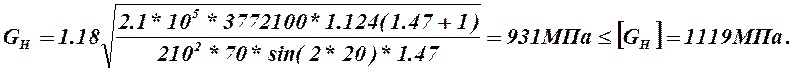
Прочность передачи по контактным напряжениям обеспечивается.

Проверка передачи по напряжением изгиба [2.c.108]

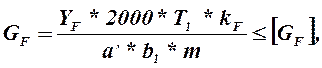                              (2.41)

где - коэффициент нагрузки[2.c.111];

                                        (2.42)

 - коэффициент неравномерности распределения нагрузки по длине зуба[2.c.111];

 - коэффициент динамической нагрузки[2.c.111];

- коэффициент формы зуба[2.c.120];

;;

Находим отношения

Расчет ведем по шестерне.

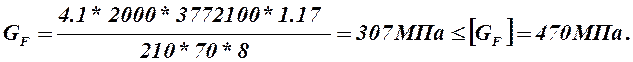
Условие прочности выполняется.

2.4.1Расчёт второй цилиндрической передачи поворотного редуктора.

Материал шестерни сталь 20ХН3А(цементация, закалка, низкий отпуск) твёрдостью  НRC 56...63, материал колеса сталь 20ХН3A(цементация, закалка, низкий отпуск) твёрдостью НRC 56...63. Передаваемая мощность  кВт; коэффициент ширины колеса ; частота вращения шестерни , колеса .

Пределы контактной выносливости для шестерни и колеса[2.c.146.]

 МПа;           (2.43)

 МПа;          (2.44)

        Допускаемые контактные напряжения для шестерни и колеса[2.c.146.]

,                         (2.45) где - коэффициент безопасности для колёс, прошедших улучшение и нормализацию[2.c.146.], ;

-коэффициент долговечности[2.c.146.], =1;

для шестерни

 МПа;

для колеса

 МПа.

Допускаемые напряжения при изгибе колеса и шестерни при расчете на усталость

МПа,                         (2.46)

где - предел выносливости зубьев по напряжением изгиба [2.с.147],

- коэффициент безопасности,

Допускаемые напряжения при изгибе

Определение основных параметров передачи.

Межосевое расстояние передачи [2.c.115]

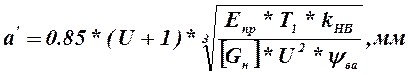                (2.47)

где -приведенный модуль упругости материала колеса;

- коэффициент ширины колеса относительно межосевого расстояния[2.c.117];

- коэффициент неравномерности распределения нагрузки по длине зуба[2.c.111];

- вращающий момент на колесе.

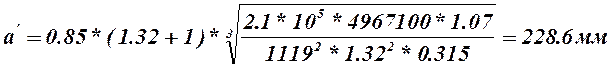
Принимаем

Ширина колеса  

Принимаем .

Диаметры начальных  окружностей колеса

              (2.48)

                  (2.49)

Задаем число зубьев шестерни

.

Число зубьев колеса

.                     (2.50)

Нормальный модуль

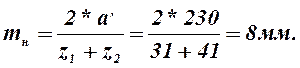                  (2.51)

Проверка передачи по контактным напряжениям.

Условие прочности имеет вид[2.c.144]

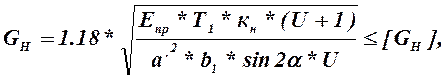       (2.52)

где - коэффициент нагрузки.

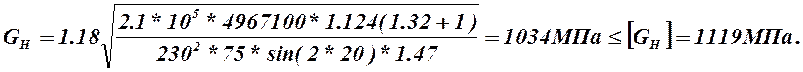
Прочность передачи по контактным напряжениям обеспечивается.

Проверка передачи по напряжением изгиба [2.c.108]

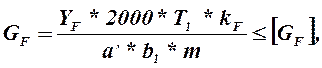                      (2.53)

где - коэффициент нагрузки[2.c.111];

                                  (2.54)

 - коэффициент неравномерности распределения нагрузки по длине зуба[2.c.111];

 - коэффициент динамической нагрузки[2.c.111];

- коэффициент формы зуба[2.c.120];

;;

Находим отношения

Расчет ведем по шестерне.

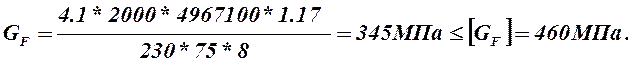
Условие прочности выполняется.

2.4.3.Расчет оси.

Расчетная схема оси приведена на рисунке

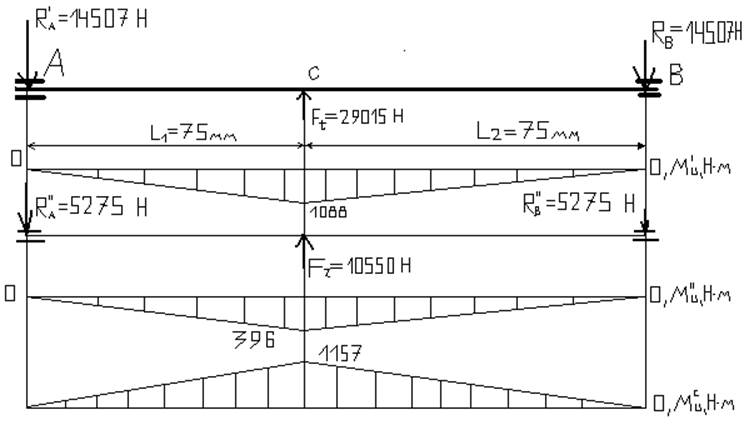
Рисунок. Расчетная схема.

Силы в зацеплении зубчатого колеса на оси:

- окружная

             (2.55)

- радиальная

                     (2.56)

где - угол зацепления.

Силы реакции опор в точке В в вертикальной плоскости определим из суммы моментов относительно точки А 

            (2.57)

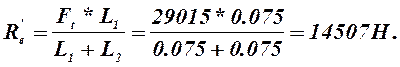               (2.58)

Силы реакции опор в точке А в вертикальной плоскости определим из суммы моментов относительно точки В 

             (2.59)

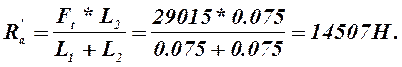               (2.60)

Проверка:

Изгибающие моменты в характерных точках(А,В и С)

Силы реакции опор в точке В в горизонтальной плоскости определим из суммы моментов относительно точки А 

                (2.61)

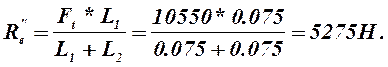                   (2.62)

Силы реакции опор в точке А в горизонтальной плоскости определим из суммы моментов относительно точки В 

                (2.63)

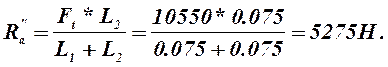                 (2.64)

Проверка:

Изгибающие моменты в характерных точках(А,В и С)

Суммарные изгибающие моменты в характерных точках(А,В и С)

Как видно из эпюры изгибающих моментов наиболие нагруженным является сечение под зубчатым колесом.

Эквивалентный момент в сечении

                (2.65)

Требуемый диаметр вала из условия прочности по эквивалентному