Иногда используются и многошаговые итерационные методы, в которых x(k+1) определяется через значения x на двух и более предыдущих итерациях.
Очень часто для ускорения сходимости в итерационные методы вводят числовые параметры tk , которые зависят, вообще говоря, от номера итераци. Способ выбора итерационных параметров определяется при
7
исследовании сходимости метода, когда выясняется при каких значениях параметров метод сходится и при каких значениях параметров сходимость будет наиболее быстрой (соответствующие параметры называются оптимальными). Для исследования сходимости удобнее записывать итерационные методы не в координатной, а в матричной форме, придерживаясь стандартной формы записи итерационных методов
Канонической формой одношагового итерационного метода решения СЛАУ называется его запись в виде
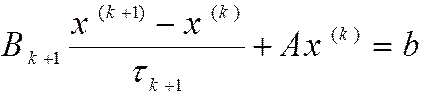
где Bk+1 - матрица, задающая тот или иной итерационный метод, tk+1 - итерационный параметр. Предполагается, что существуют обратные матрицы [Bk+1]-1. Итерационный метод называют явным, если стационарным, ес Bk+1 - единичная матрица. Неявные итерационные методы имеет смысл применять лишь в том случае, когда каждую матрицу Bk обратить легче, чем исходную матрицу A (т. е. когда решение системы уравнений с матрицей Bk требует меньше машинной памяти или времени или алгоритмически проще, чем решение исходной системы).
Итерационный метод называется ecли Bk+1=B и tk+1=t,
(т.е. не зависят от номера итерации), и нестационарным - в противоположном случае. Согласно этой
классификации метод простой итерации является одношаговым явным стационарным
методом с диагональной матрицей B
(bii.= aii) и может быть записан в
виде 
, где r(k) - вектор невязки.
На практике используют три способа определения окончания итераций.
При первом определяют величину стабилизации и прекращают вычисления,
если она меньше e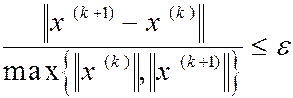 
.
Недостатком этого способа является то, что при медленно сходящихся итерациях
величина стабилизации может быть малой, хотя приближенное решение сильно
отличается от точного.
При втором способе вычисляют нормы невязки до начала итераций и
на каждой итерации. При выполнении неравенства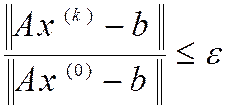 
итерации прекращают.
При третьем способе предварительно оценивается число итераций, необходимое для получения заданной точностиe. Если для погрешности
8
итерационного метода выполняются оценки
,
где qÎ (0,1), то говорят, что метод сходится со скоростью геометрической прогрессии
со знаменателем q. Можно определить число итераций, достаточное
для того, чтобы начальная погрешность уменьшилась в заданное число раз,
потребовав, чтобы qn
< e :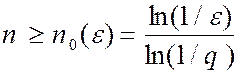 
Целая часть числа n0(e) называется минимальным числом итераций, необходимым для получения заданной точности e.
Величину ln(1/q) называют скоростью сходимости итерационного метода. Скорость сходимости целиком определяется методом и не зависит ни от номера итерации, ни от выбора начального приближения, ни от задаваемой точности. Качество различных итерационных методов сравнивают обычно по их скорости сходимости: чем выше скорость сходимости, тем лучше метод.
Для данной СЛАУ условия сходимости не выполняются .Диагонального преобладания можно добиться с помощью эквивалентных преобразований матрицы системы:
9
2.2 Список идентификаторов:
В программе |
В формуле |
|
|
eps |
e |
|
|
AN |
G |
|
X0 |
XO |
|
Bn(n) |
f |
|
|
it |
n |
|
Остальные идентификаторы являются промежуточными .
12
Описание алгоритма основной программы:
№ блока Описание
5, 8, 11 Программа запрашивает у пользова- теля числовые значения n.
4,7,10 . Программа читает введённые числовые значения n.
6,8,12,14,
17,18,23,
29,
20,25
1,33
Цикл FOR осуществляет ввод и запись значений основных и промежуточных переменных.
Циклы if, которые осуществляют проверку каждого из условий и обраща- ются к соответствующим процедурам.
.
Начало,конец программы.
13
2.4. Распечаткатекстапрограммы:
program kurs;
uses crt;
type
ty1=array[1..3] of string;
var
df:Word;
ch:Char;
const
men1:ty1=(' Справка ',
' Вычисления ',
' Выход ');
{----------------------------------------------------------------------------}
PROCEDURE ZASTAVKA;
begin
textcolor(14);
textbackground(15);
clrscr; textcolor(0);
writeln(' БНТУ');
writeln;
writeln(' Кафедра "Горные Машины"');
writeln(' гр. ');
writeln;
writeln;
writeln;
writeln;
textcolor(0);
writeln(' Программа решения ');
writeln(' системы линейных уравнений ');
writeln(' методом итераций ');
writeln;
textcolor(0);
writeln(' Курсовая работа');
writeln;textcolor(0);
writeln(' по дисциплине "Информатика"');
writeln;
writeln;
writeln;
textcolor(0);
14
writeln(' Выполнил : ');
writeln;
writeln(' Руководитель: ');
writeln; textcolor(0);
writeln;
writeln(' Минск 2002');
textcolor(0+16);
write (' для продолжения нажмите любую клавишу');
readkey;
end;
{------------------------------------------------------------------------}
procedure spravka;
begin
textmode(12);textbackground(1);clrscr;
{ Формирование окна справки}
window(3,3,77,23);textbackground(7);clrscr;gotoXY(30,2);write('С П Р А В К А :');
gotoXY(27,2);textcolor(12);
textcolor(0);gotoXY(2,4);
writeln(' Программа создана для решения системы линейных уравнений ');
writeln(' методом простых итераций. ');
writeln;
writeln(' Для вычисления данной системы необходимо выбрать ');
writeln(' пункт меню ''Вычисления'',затем по запросу программы ');
writeln(' ввести исходные параметры - коэффициенты при ');
writeln(' переменных Х ( по столбцам ) ,а также ');
writeln(' свободные члены b уравнения. ');
writeln(' После этих операций на экран будут выведены ');
writeln(' результаты итераций и погрешность вычислений. ');
gotoXY(25,20);textcolor(16+0);
writeln('для выхода нажмите любую клавишу...');
readkey;
end;
{------------------------------------------------------------------------}
15
procedure run;
const eps=0.001; {Требуемая точность}
MAX=20;
var n,i,j,it: integer;
d,de,s: real;
x,x0,b,bn,bp: array[1..MAX]of real;
a,an,ap: array[1..MAX,1..MAX]of real;
begin
clrscr;
writeln(' Решение СЛАУ методом простой итерации (|A|*|x|=|b|)');
write(' Введите число уравнений n:');
readln(n);
for i:=1 to n do
for j:=1 to n do
begin
write('Введите A[',i,',',j,']:');
readln(a[i,j]);
end;
for i:=1 to n do
begin
write('Введите b[',i,']:');
readln(b[i]);
end;
begin
for i:=1 to n do begin
an[i,1]:=a[i,1]+a[i,3]; end;
for i:=1 to n do begin
an[i,2]:=a[i,1]*(-1)+a[i,2] end;
for i:=1 to n do begin
an[i,3]:=a[i,2]*(-2)+a[i,3];end;
for i:=1 to n do begin
ap[i,4]:=a[i,3]*(-2)+a[i,4];end;
for i:=1 to n do begin
an[i,4]:=ap[i,4]+an[i,2]; end;
begin
bn[1]:=b[3]+b[1];
bn[2]:=b[1]*(-1)+b[2];
bn[3]:=b[2]*(-2)+b[3];
bp[4]:=b[3]*(-2)+b[4];
bn[4]:=bp[4]+bn[2];
end;
for i:=1 to n do
16
begin
x0[i]:=0;
x[i]:=0;
end;
it:=0;
repeat
de:=0;
for i:=1 to n do
begin
s:=bn[i];
for j:=1 to n do
if j<>i then s:=s-an[i,j]*x0[j];
s:=s/an[i,i];
d:=abs(x[i]-s);
x[i]:=s;
if d>de then de:=d;
end;
inc(it);
for i:=1 to n do
x0[i]:=x[i];
if it mod 10=0 then readln;
write('Итерация:',it:4);
for i:=1 to n do
write(' x',i,'=',x[i]:4:1);
writeln(' de=',de:4:5);
until (it>200)or(de<eps) or (de>30000);
if (de>20000) then writeln('Данным методом СЛАУ не решаеться!') else
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
