Расчет зубчатых и цепных передач. Выбор материала и назначение допускаемых напряжений. Значения базового числа циклов нагружения

5. Расчет зубчатых и цепных передач

5.1 Расчет зубчатых передач

5.1.1Выбор материала и назначение допускаемых напряжений

При выборе материала для шестерни и колеса следует ориентироваться на применение одной и той же марки стали, но с различной термической обработкой, чтобы твердость шестерни была не менее чем на 20… 30 единиц НВ больше твердости колеса при прямых зубьях и более 40 единиц НВ – при косых и шевронных зубьях.

При твердости шестерни и колеса 45НRC и более не требуется обеспечивать повышенную твердость материала шестерни.

Рекомендации по применению незакаленных (с твердостью до 350 НВ) и закаленных (с твердостью активных поверхностей зубьев более 350НВ) приведены в [1], c.11…12.

Механические характеристики сталей для зубчатых колес приведены в табл.1. Для сравнения твердости, выраженной в единицах НВ и НRC, можно пользоваться зависимостью: 1 HRC≈10HB.

По рекомендациям из справочных таблиц принимаем для изготовления шестерни и колес сталь 40Х улучшенную со следующими механическими характеристиками:

Шестерня                     

Колесо                          

Значения базового числа циклов нагружения N_Hlim=30(НВ)^2,4<120∙10⁶ или см. ГОСТ 21354-87, рис.2.1 в зависимости от средней твердости.

Для шестерни N_Hlim=1,97∙10⁷ циклов.

Для колеса  N_Hlim=1,56∙10⁷ циклов.

Эквивалентное число циклов перемен напряжений:

                      N_K=60Σ(T_i/T_max)^m·n·L_H·C ,                                                          (5.1)

где n – частота вращения шестерни (колеса), мин^-1; L_H- срок службы передачи под нагрузкой, ч; C – число зацеплений (число одинаковых зубчатых колес, одновременно находящихся в зацеплении с данной шестерней (колесом); T_i,T_max,L_Hi- заданы циклограммой нагружения (T_max- наибольший длительно действующий момент); m – показатель степени, m=3.

         ч;       

 - колесо в зацеплении внешнем;

 - частота вращения вала шестерни.

 - частота вращения вала колеса.

Согласно циклограмме нагружения для шестерни:

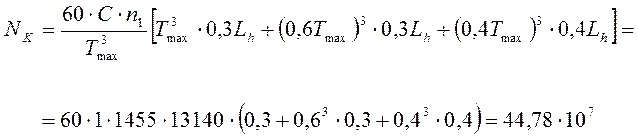
Для колеса:

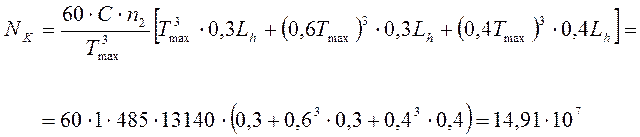
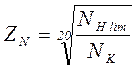                                                                                                  (5.2)

Для колеса:

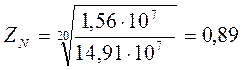
Для шестерни:

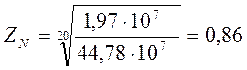
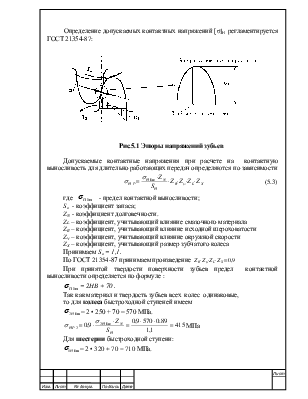
Определение допускаемых контактных напряжений [σ]_H регламентируется ГОСТ 21354-87:

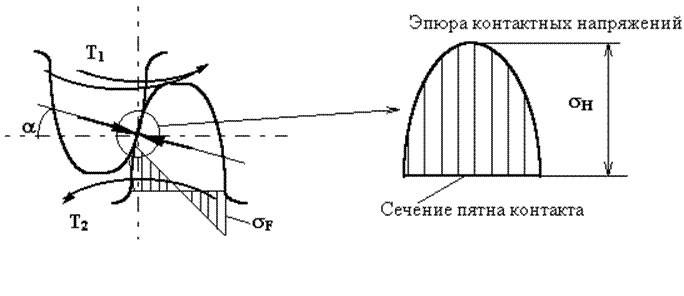Рис.5.1 Эпюры напряжений зубьев

Допускаемые контактные напряжения при расчете на  контактную выносливость для длительно работающих передач определяются по зависимости

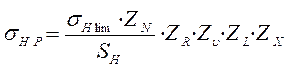                                                                        (5.3)

где      - предел контактной выносливости;

S_н  - коэффициент запаса;

Z_N - коэффициент долговечности.

Z_L– коэффициент, учитывающий влияние смазочного материала

Z_R– коэффициент, учитывающий влияние исходной шероховатости

Z_V– коэффициент, учитывающий влияние окружной скорости

Z_X– коэффициент, учитывающий размер зубчатого колеса

Принимаем S_н = 1,1.

По ГОСТ 21354-87 принимаем произведение

При принятой твердости поверхности зубьев предел  контактной выносливости определяется по формуле :

= 2HB + 70 .

Так как материал и твердость зубьев всех  колес  одинаковые, то для колеса быстроходной ступеней имеем

= 2 • 250 + 70 = 570 МПа.

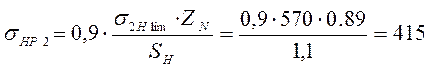МПа

Для шестерни быстроходной ступени:

= 2 • 320 + 70 = 710 МПа.

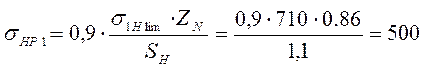МПа

Для прямозубых передач, коими являются передачи на быстроходной ступени имеем:

σ_HP=min(σ_HP1;σ_HP2)= σ_HP2=415 МПа

Допускаемое напряжение изгиба определяется по формуле:

;

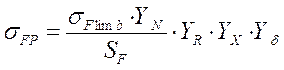где    - предел выносливости зубьев при изгибе,

 - коэффициент безопасности, , принимаем , т.к. большие значения принимаются для литых заготовок;

 - коэффициент долговечности, ,

Y_R– коэффициент, учитывающий влияние исходной шероховатости Y_R=1

Y– коэффициент, учитывающий чувствительность материала Y=1

Y_X– коэффициент, учитывающий размер зубчатого колеса Y_X=1

Для шестерни:

;

Для колеса:         

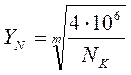                                         ,                                                      (5.4)

здесь m – показатель степени, зависящий от твердости: m=6 при твердости <350НВ; m=9 при твердости >350НВ; N_K – эквивалентное число циклов нагружения зубьев за весь срок службы передачи, определяемое по формулам но при этом в формуле  m=6 при твердости <350НВ; m=9 при твердости >350НВ.

Для шестерни быстроходной ступени:

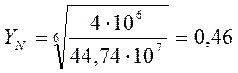
Принимаем

Для колеса быстроходной ступени:

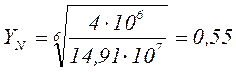
Принимаем

Допускаемое напряжение изгиба для шестерни:

МПа

МПа

Принимаем 

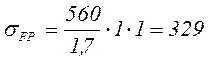МПа

Допускаемое напряжение изгиба для колеса:

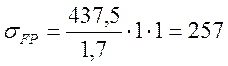МПа

МПа

[F] = min(1, 2) = 257 МПа

5.1.2. Проектировочный расчет быстроходной ступени с коническими колесами

В быстроходной ступени используется коническая передача с прямыми зубьями.

Диаметр основания делительного конуса колеса определяется  из  условия   контактной выносливости по формуле

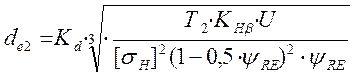  ,                                       (5.5)

где Т - момент на валу колеса передачи;

=99;

u- передаточное число быстроходной ступени;

 - коэффициент, длины зуба конического колеса

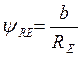обычно принимают равным 0,285.                                        (5.6)

[ s_H]  - допускаемое контактное напряжение.                                          

Здесь K_Hb - коэффициент неравномерности распределения нагрузки по длине контактных линий.

K_Hb =1,38  по графику.

Произведя подстановку, по формуле (5.5) получи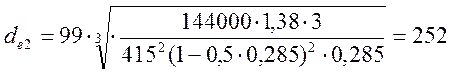м

 мм.

Диаметр d_e2 округляем до значения согласно единому ряду параметров d_e2  = 250 мм.

Принимаем число зубьев шестерни

Z₁=22, тогда число зубьев колеса

Z₂ = Z₁ · u = 22 · 3 = 66.

Относительное смещение для шестерни при Z₁ = 22 и u = 3 [ 1 ]

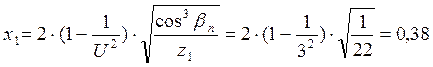
для колеса   x₂ = - x₁ = - 0,38.

Выполняем геометрический расчет конической передачи.

Внешний окружной модуль определяем по формуле (“Курсовое проектирование  по деталям машин”,  Чернавский, стр. 341)

                                        m_e = d_e2/Z₂=250/66=3,79 мм.

Средний окружной модуль

m = m_e · (1-0,5·Кbe)= 3,79·(1-0,5·0,3) = 3,22 мм.

Углы делительных конусов:

d₂ = arctg u = arctg 3 = 71,58^o ;

d₁  = 90^о - d₂  = 18,42^о.

Внешнее конусное расстояние:

мм.                       (5.9)

Ширина зубчатого венца

bw= Kbe·R_e = 0,3·131,84 = 39,6 мм.

bw=10 · m_e=10·3.79=38 мм.

Принимаем bw= 38 мм.

Среднее конусное расстояние

Rm = R_e - 0,5·bw = 131,84 - 0,5·38 = 112,8 мм.

Коэффициент радиального зазора с٭ = 0,2

Коэффициент высоты головки  ha٭ = 1

Угол профиля α = 20^o .

Радиальный зазор

С=0,2 · m_e = 0,2 · 3,79 = 0,758

Внешняя высота головки зуба в среднем сечении

h_aе1 = (1 + x₁)·m_е = (1 + 0,38)·3,79 = 5,23 мм.

h_aе2 = (1 – x₂)·m_е = (1 - 0,28)·3,79 = 2,35 мм.

Внешняя высота зуба:

h_е = 2·m_е + c= 2∙3,79+0,758 = 8,3 мм.

Внешняя высота ножки зуба в среднем сечении

h_fе1 = h_aе2+с٭m_е = 2,35+0,2∙3,79 = 3,11 мм.

h_fе2 = h_aе1+ с٭m_е = 5,23+0,2∙3,79 = 5,99 мм.

Угол ножки зуба

q_f1 = arctg (h_fе1 / R_е)  = arctg (3,11 / 131,84) = 1,3514^o.

q_f2 = arctg (h_fе2 / R_е)  = arctg (5,99 / 131,84) = 2,6012^o.

Угол головки зуба

q_a1  = q_f2 = 2,6012^o.

q_a2  = q_f1 = 1,3514^o.

Угол конуса вершин

d_a1 = d₁ + q_a1  = 18,42 + 2,6012 = 21,0212^o.

d_a2 = d₂ + q_a2  = 71,58 +1,3514 = 72,9314^o.

Угол конуса впадин

d_f1 = d₁ - q_f1  = 18,42 - 1,3514= 17,0686^o.

d_f2 = d₂-q_f2  = 71,58 - 2,6012 = 68,9788 ^o.

Внешний делительный диаметр:

d_e1 = m_е∙z₁ = 3,79∙22 =83,38мм.

d_e2 = m_е∙z₂ = 3,79∙66 =250,14мм.

Средний делительный диаметр

d_m1 = (1-0,5K_be)∙dе₁=(1- 0,5∙0,3)∙83,38=70,87мм.

d_m2 = (1-0,5K_be)∙dе₂=(1- 0,5∙0,3)∙250,14=212,62мм.

Внешний диаметр вершин зубьев

d_ae1 = d_e1 + 2·h_ae1·cosd₁ =83,38 + 2·5,23·cos18,42 =

= 93,304 мм.

d_ae2 = d_e2 + 2·h_ae2·cosd₂ = 250,14 + 2·2,35·cos71,58  =

= 251,625 мм.

Число зубьев эквивалентного колеса.

Z_v1=z1/cosd₁=22/cos18,42=23,19

Z_v2=z2/cosd₂=66/cos71,58=208,87

Коэффициент торцевого перекрытия

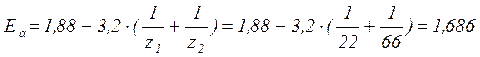
Постоянная хорда

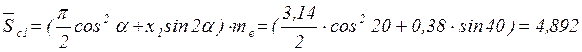
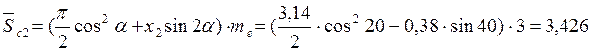
Высота до постоянной хорды

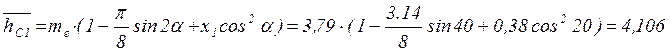
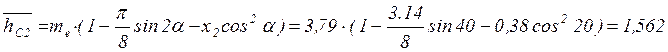
5.1.3. Проверочный расчет передач ,быстроходной ступени на контактную прочность

Уравнение для проверочного расчета контактной прочности конической передачи имеет вид:

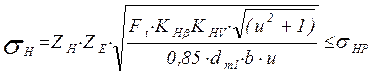                   (5.12)

где  s_H  - фактическое контактное напряжение.

Коэффициенты взяты из ГОСТ 21354-87. 

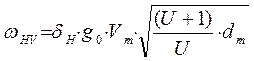
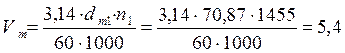 м/с

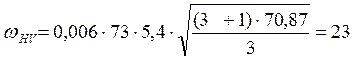
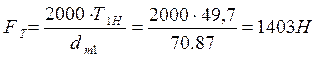
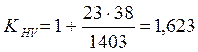
 по графику.

Подставляя значения параметров в уравнение (5.12), получим:

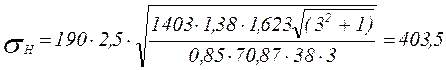 МПа.

Действующие напряжения меньше допускаемых [ s_H ]= 415 МПа, т.е. контактная прочность колеса быстроходной ступени обеспечивается.

5.1.4. Проверочный расчет передач быстроходной ступени на изгибную прочность