1. Чему равна функция выживания?
1) s(x)=1+F(x) 2) s(x)=1-f(x) 3) s(x)=1+f(x) 4) s(x)=1-F(x)
2. Какое из свойств не относится к функции выживания?
1) s(x) непрерывна слева 2) s(x) убывает 3) s(0)=1 4) s(+¥)=0
3. Чему равно значение функции выживания для предельного возраста?
1) s(x)=1 2) s(x)=-1 3) s(x)=0 4) s(x)=¥
4. Чему равно среднее число умерших в возрасте от x до x+t лет из фиксированного числа новорожденных l0 ?
1) tyx=l0(s(x)-s(x+t)) 2) tyx= l0(s(x)+s(x+t)) 3) tyx=l0(s(x+t)-s(x)) 4) tyx= l0(s(x)-s(x-t))
5. Чему равна
вероятность смерти в промежутке ![]() ?
?
1) s(x)+s(x+t) 2) s(x)-s(x-t) 3) s(x)-s(x+t) 4) s(x+t)-s(x)
6. Чему равна интенсивность смерти?
1) 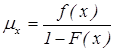 2)
2)
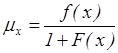 3)
3) ![]() 4)
4)
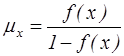
7. Какое свойство верно для интенсивности смертности?
1) 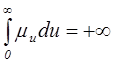 2)
2)
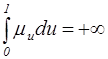 3)
3) 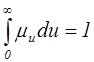 4)
4)
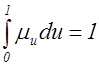
8. Пусть Х – величина, характеризующая продолжительность жизни, тогда ее мат. ожидание равно:
1) 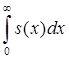 2)
2)
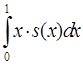 3)
3) 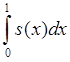 4)
4)
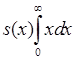
9. Какой вид имеет функция выживания в модели де Муавра
1) ![]() 2)
2) 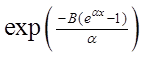 3)
3) 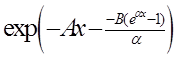 4)
4)
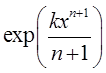
10. Какой вид имеет функция выживания в модели Гомпертца?
1) ![]() 2)
2) 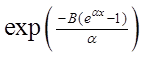 3)
3) 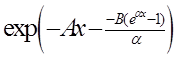 4)
4)
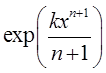
11. Какой вид имеет функция выживания в модели Мэйкхама?
1) ![]() 2)
2) 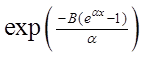 3)
3) 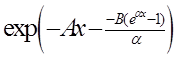 4)
4)
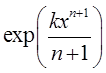
12. Какой вид имеет функция выживания в модели Вейбулла?
1) ![]() 2)
2) 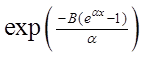 3)
3) 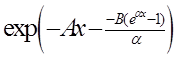 4)
4)
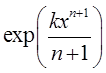
13. Какая из приведенных ниже функций может рассматриваться как кривая смертей?
1)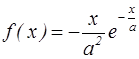 2)
2)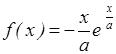 3)
3)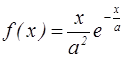 4)
4)![]()
14. Чему равна функция выживания, если кривая
смертей имеет вид 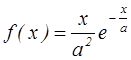 ?
?
1) 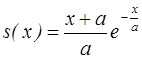 2)
2)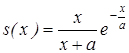 3)
3)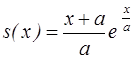 4)
4)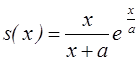
15. Чему равна интенсивность смертности, если
кривая смертей имеет вид 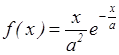 ?
?
1) 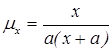 2)
2) 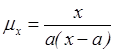 3)
3) 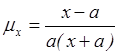 4)
4) 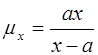
16. Найти среднее число представителей исходной группы в l0=10000 новорожденных, которые умрут в возрасте от 40 до 100 лет (принять s(40)=0,949, s(100)=0,012 )?
1) 60y40=9370 2) 40y100=9700 3) 40y60=9730 4) 60y100=9670
17. Найти дисперсию числа представителей исходной группы в l0=10000 новорожденных, которые умрут в возрасте от 40 до 100 лет (принять s(40)=0,949, s(100)=0,012 )?
1) D[60Y40]=590,31 2) D[60Y40]=590,01 3) D[40Y100]=590,31 4) D[40Y100]=590,01
18. Пусть T(x)=X-x – остаточное время жизни (здесь х – возраст, Х – продолжительность жизни). Найти вероятность Р(Т(х) £ t).
1)![]() 2)
2) ![]() 3)
3) 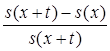 4)
4) 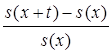
19. . Пусть T(x)=X-x – остаточное время жизни (здесь х – возраст, Х – продолжительность жизни). Чему равна плотность распределения случайной величины Т(х)?
1) 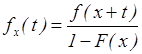 2)
2) 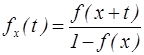 3)
3) 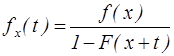 4)
4) 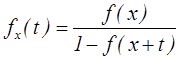
20. Пусть T(x)=X-x – остаточное время жизни (здесь х – возраст, Х – продолжительность жизни). Найти вероятность Р(Т(х) > t).
1)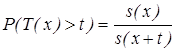 2)
2) ![]() 3)
3) ![]() 4)
4)
![]()
21. Среднее значение остаточного времени жизни человека в возрасте х лет?
1)Продолжительность жизни 2)Вероятная Продолжительность жизни
3)Полная Продолжительность жизни 4) Полная вероятная Продолжительность жизни
22. Зная значения функции выживания определить вероятность того, что остаточное время жизни 10 лет лежит в промежутке от 20 до 40 лет (принять s(10)=0,983, s(30)=0,965, s(50)=0,915)?
1). 0,051 2). 0,052 3). 0,049 1). 0,050
23. Зная, что в возрасте от 20 до 30 лет
интенсивность смерти описывается формулой ![]() ,
подсчитайте величину 2q20?
,
подсчитайте величину 2q20?
1)0,575 2)0,574 3)0,576 4)0,572
24. Зная, что смертность описывается законом 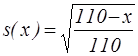 , подсчитать вероятность того, что
человек в возрасте 30 лет умрет в течение ближайших 2-х лет?
, подсчитать вероятность того, что
человек в возрасте 30 лет умрет в течение ближайших 2-х лет?
1) 0,013 2)0,011 3)0,015 4)0,017
25. Зная, что смертность описывается законом 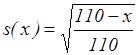 , подсчитать среднее остаточное время
жизни человека в возрасте 30 лет?
, подсчитать среднее остаточное время
жизни человека в возрасте 30 лет?
1)53,33 2)52,33 3)53,35 4)53,23
26. Рассчитайте вероятность смерти женщины в возрасте 31 года (принять ух=108, lх=95236)?
1) q31=0,001 2) q31=0,002 3) q31=0,003 4) q31=0,004
27. Чему равна единовременная нетто-ставка по дожитию?
1)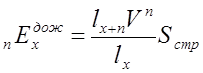 2)
2) 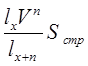 3)
3) 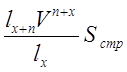 4)
4) 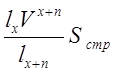
28. Чему равна единовременная нетто-ставка по дожитию?
1) 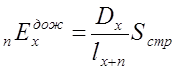 2)
2) 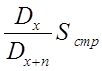 3)
3) 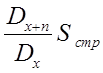 4)
4)
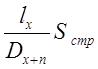
29. Чему равна годичная нетто-ставка постнумерандо?
1) 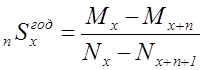 2)
2) 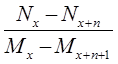 3)
3) 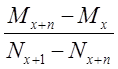 4)
4)
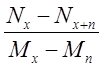
30. Рассчитайте брутто-ставку, если известно, что нетто ставка равна 0,05, а доля нагрузки в составе брутто-ставки равна 0,075?
1) 0,054 2) 0,053 3) 0,055 4) 0,052
Индексный метод
1)Относительный статистический показатель, который обобщает относительное изменение одной переменной или группы переменных, называют
1) Индексом 2)Средней величиной 3)Корреляцией 4)Дисперсией
2)Индекс – это
1)Относительный статистический показатель, который обобщает относительное изменение одной переменной или группы переменных. 2)Относительный статистический показатель, который обобщает относительное изменение одной переменной по отношению к другой 3)Относительный статистический показатель, который показывает абсолютное изменение переменной 4)Относительный статистический показатель, который отношение одной переменной к группе других
3)Индивидуальный индекс характеризует
1)Изменение явления, состоящего из однородных элементов, и представляют собой обычную относительную величину динамики показателя 2)Изменение явления, состоящего из разнородных непосредственно не суммируемых элементов 3)Отношение одного явления к группе других элементов 4)Изменение явления, состоящего из однородных и разнородных элементов
4)Сводный индекс характеризует
1)Изменение явления, состоящего из однородных элементов, и представляют собой обычную относительную величину динамики показателя 2)Изменение явления, состоящего из разнородных непосредственно не суммируемых элементов 3)Отношение одного явления к группе других элементов 4)Изменение явления, состоящего из однородных и разнородных элементов
5)Индекс, характеризующий изменение явления, состоящего из однородных элементов, и представляют собой обычную относительную величину динамики показателя, называют
1)Сводным 2)Индивидуальным индексом 3)Индексом Ласпейреса 4)Индексом Пааше
6)Индекс, характеризующий изменение явления, состоящего из разнородных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.