Уравнение Эйлера движения идеальной жидкости. Уравнение неразрывности. Интеграл Бернулли

Мат. методы в естествознании

1.1. Какое из приведенных ниже высказываний является верным?

A)  В случае потенциального течения несжимаемой жидкости потенциал является гармонической функцией.

B)  В случае потенциального течения несжимаемой жидкости потенциал является решением волнового уравнения.

С) Потенциальное течение жидкости является установившимся.

1.2. Для нестационарного течения в общем случае

A)  траектории частиц совпадают с линиями тока.

B)  траектории частиц не совпадают с линиями тока.

C)  линиитокасовпадаютсвихревымилиниями.

1.3. Уравнение Эйлера движения идеальной жидкости следует из A) закона изменения количества движения.

B) закона изменения момента количества движения. C) закона сохранения массы.

1.4. Уравнение неразрывности имеет вид

A)

B)

C)

1.5. Уравнение Эйлера движения идеальной жидкости имеет вид

A)  gradp + ρF.

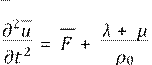
B)  gradp+ρF +(λ+µ)graddivv+ µ∆v.

C)  graddiv.

1.6. Взадачахостационарныхпотенциальных течениях идеальной несжимаемой жидкости

A)  распределение скоростей находится из уравнения Эйлера, а для нахождения распределения давлений используется интеграл Бернулли.

B)  распределение скоростей находится из уравнения Лапласа, а для нахождения распределения давлений используется интеграл Бернулли.

C)  распределение скоростей находится из волнового уравнения, а для нахождения распределения давлений используется интеграл Коши-Лагранжа.

1.7. Какаяизуказанныхфункцийнеможетслужитьпотенциаломтечениянесжимаемой жидкости?

A)  .

B)  .

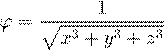C)  .

1.8. Какое из приведенных ниже выражений является верным?

A)  + grad

B)  = grad

C)  + gradgrad.

1.9. Интеграл Бернулли имеет вид:

A)  .

B)  . v2

C)   + P + U = C.

2

1.10. ИнтегралЛагранжа — Кошиимеет вид:

A)  .

B)  . v2

C)   + P + U = C.

2

2.1. Уравнение Навье-Стокса движения линейно-вязкой жидкости следует из A) закона изменения количества движения.

B) закона изменения момента количества движения. C) закона сохранения массы.

2.2. Уравнение Навье-Стокса движения линейно-вязкой жидкости имеет вид

A)  gradp + ρF.

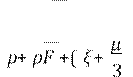
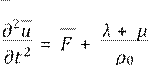
B)  grad )graddivv+ µ∆v.

C)  graddiv.

2.3. Условия прилипания на абсолютно твердой поверхности заключаются A) в равенстве нулю нормальной скорости.

B)  в равенстве нулю вектора скорости.

C)  в непрерывности вектора скорости.

2.4.   Число Рейнольдса определяется выражением

A)  .

B)  . C) .

2.5. Число Эйлера определяется выражением

A)  .

B)  . C) .

2.6. Число Фруда определяется выражением

A)  .

B)  . C) .

2.7. В безразмерном виде справедлива запись: v A) ∆.

B)  ∆.

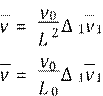0

2

C)  ∆.

2.8. Одним из результатов теории пограничногослояявляетсяутверждение: A) скорость внутри пограничного слоя не меняется.

B)  давление внутри пограничного слоя не меняется в направлении нормали к контуру поверхности.

C)  давление внутри пограничного слоя не меняется.

2.9. Толщина пограничного слоя определяется выражением:

A)  .

B)  .

C)  .

2.10. Течение Куэтта — это A) течение идеальной жидкости между пластинами, одна из которых неподвижна, а другая движется с постоянной скоростью.

B) течение вязкой жидкости между пластинами, одна из которых неподвижна, а другая движется с постоянной скоростью. С) течение вязкой жидкости между движущимися пластинами.

3.1.   Уравнение Ламе движения линейно-упругого тела следует из A) закона изменения количества движения.

B) закона изменения момента количества движения. C) закона сохранения массы.

3.2.   Уравнение Ламе движения линейно-упругого тела в случае малых деформаций имеет вид

A)  gradp + ρF.

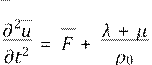
B)  grad)graddivv+ µ∆v.

C)  graddiv.

3.3. Обобщенный закон Гука устанавливает связь между

A)  тензором напряжений и тензором деформаций.

B)  тензором напряжений и тензором скоростей деформаций.

C)  тензором скоростей деформаций и тензором деформаций.

3.4. Закон Гука справедлив A) для малых деформаций.

B) для больших деформаций.

С) для больших и малых деформаций.

3.5. Функция Эйри используется при решении

A)  пространственных задач статики упругого тела.

B)  плоских задач статики упругого тела.

C)  плоских динамических задач теории упругости.

3.6. Функция напряжений в плоских задачах упругого равновесия связана с компонентами тензора напряжений соотношениями

A)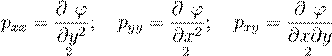. B). C).

3.7. Уравнения Бельтрами — Мичела используются

A)  в задачах статики упругого тела в напряжениях.

B)  в задачах статики упругого тела в смещениях.

C)  в задачах динамики упругого тела в напряжениях.

3.8. Модуль Юнга определяется выражением:

λ

A).

B)  .

C)  λdivu.

3.9. Коэффициент Пуассона определяется выражением:

A)  .

B)  .

C)  λdivu.

3.10. Модули упругости µ характеризует

A)  деформацию сдвига.

B)  объемное расширение.

C)  продольное растяжение.

4.1. Распространение звуковых волн в идеальной жидкости в установившемся режиме движения описывается:

A)  ∆.

B)  ∆   = 0;       ∆ .

C)  ∆.

4.2. Распространение звуковых волн в вязкой жидкости в установившемся режиме движения описывается:

A)  ∆.

B)  ∆   = 0;       ∆ .

C)  ∆.

4.3. Нестационарное распространение звуковых волн в идеальной жидкости описывается:

A)  ∆.

B)  ∆   = 0;       ∆ .

C)  ∆.

4.4. В продольных волнах смещения частиц происходят

A)  в направлении распространения волны.

B)  в направлении, перпендикулярном направлению распространения волны. C) в произвольном направлении.

4.5. В поперечных волнах смещения частиц происходят

A)  в направлении распространения волны.

B)  в направлении, перпендикулярном направлению распространения волны. C) в произвольном направлении.

4.6. Математическая модель распространения упругих волн в установившемся режиме колебаний имеет вид:

A)  ∆.

B)  ∆ψ + k₁²ψ = 0;        ∆ .

∂2

C)  ∆.

4.7. Вязкие волны являются A) продольными.

B)  поперечными.

C)  медленнозатухающими.

4.8. Уравнения распространения упругих волн выводятся A) из уравнения Эйлера.

B)  из уравнения Ламе.

C)  из уравнения Лапласа.

4.9. Распространение электромагнитных волн описывается A) уранениями Навье — Стокса.

B)  уравнениями Максвелла.

C)  уравнениями Лапласа.

4.10. Граничные условия в задачах дифракции звуковых волн на абсолютно жестких телах в идеальной жидкости состоят

A)  в равенстве нулю давления на поверхности тела.

B)  в равенстве нулю скорости частиц на поверхности тела.

C)  вравенственулюнормальнойскорости частиц на поверхности тела.