Уравнение теплопроводности для стержня. Каноническая форма линейного уравнения гиперболического типа, страница 2

B)  сводитсякзадачесоднороднымиграничными условиями для чего строится функция

24. Задача  при неоднородных граничных условиях на границе области и начальном условии u(ρ,0) = ϕ(ρ), ρ = ρ(x,y,z) решается:

A)  сразу применением метода Фурье.

B)  сводится к задаче с однородными граничными условиями, дял чего подбирается функция W (ρ,t), удовлетворяющая граничным условиямм и имеющая непрерывные вторые производные.

25. Задача

) = 0;

u_x (l,t) = A, A − const. есть:

A)  первая краевая задача для волнового уравнения.

B)  вторая краевая задача для волнового уравнения.

C)  смешанная краевая задача для волнового уравнения.

D)  смешаннаякраеваязадачадляуравнения теплопроводности.

26.                        Задача      u_tt                =            a²∆u           +

Asinωt, u(r,ϕ,t)|_r=1 = 0, u(r,ϕ,0) = u_t (r,ϕ,0) есть:

A)  первая краевая задача для волнового уравнения на отрезке 0 ≤ r ≤ 1.

B)  первая краевая задача для волнового уравнения в круге радиуса r = 1. C) задача Дирихле для круга.

27.               Задача u_xx          =        u_tt, u(x,0)        =            x +

1; u_t (x,0) = 0; u_x (0,t) = t, u(1,t) = t + 1 есть:

A)  первая краевая задача для волнового уравнения на отрезке (0,1).

B)  вторая краевая задача для волнового уравнения на отрезке (0,1).

C)  Смешаннаякраеваязадачадялуравнения теплопроводности на отрезке (0,1).

D)  Смешаннаякраеваязадачадялволнового уравнения на отрезке (0,1).

28.              Задача u_tt         =        u_xx − 4u, 0        <     x          <

1, u(x,0) = x² − 1; u_t (x,0) = 0; u_x (0,t) =

0; u_x (l,t) = −hu(l,t) есть:

A)  первая краевая задача для волнового уравнения.

B)  вторая краевая задача для волнового уравнения.

C)  смешанная краевая задача для волнового уравнения.

D)  третья краевая задача для волнового уравнения.

29. Задача u_tt = a²u_xx, 0 < x < l, t > 0, u(x,0) = 0; u_t (x,0) = x² + 1; u_x (0,t) =

0; u_x (l,t) = −hu(l,t) есть:

A)  первая краевая задача для волнового уравнения.

B)  вторая краевая задача для волнового уравнения.

C)  третья краевая задача для волнового уравнения.

D)  смешанная краевая задача для волнового уравнения.

30. Уравнение u_xx + u_yy = −xy есть: A) волновое уравнение.

B)  уравнение Лапласа.

C)  уравнение Пуассона.

31. Уравнение Пуассона ∆u = f (x,y) в круге радиуса a с граничным условием u|_r=a = 0 решается:

A)  сразу применением метода Фурье.

B)  полагается u = v + w, где v – частное решение уравнения Пуассона, а w – решение уравнения Лапласа ∆w = 0.

32. Для определения стационарной температуры в теле необходимо решить: A) уравнение Пуассона.

B)  уравнение Лапласа.

C)  уравнение теплопроводности.

33. Для определения функции, гармонической внутри круга необходимо решить: A) волновое уравнение.

B)  уравнение теплопроводности.

C)  уравнение Лапласа. 34. Задача корректно поставлена, если A) она имеет решение.

B)  решение единственное.

C)  решение существует, единственное и малые изменения исходных данных влекут за собой малые изменения решения.

35. Поставить краевую задачу в малых поперечныхколебанияхструны, предполагается, что левый конец струны закреплен, в правый свободен.

A)  u_tt             =            a²u_xx, 0               <            x             <            l, u(x,0)              =

ϕ(x), u_t (x,0) = ψ (x); u(0,t) = u(l,t) = 0;

B)  u_tt = a²u_xx, 0 < x < l, u(x,0) = ϕ(x), u_t (x,0) = ψ (x); u(0,t) = 0;u_x (l,t) = 0;

C)  u_tt = a²u_xx, 0 < x < l, u(x,0) = ϕ(x), u_t (x,0) = ψ (x); u_x (0,t) = 0;u_x (l,t) =

0;

36. Как решается уравнение теплопроводности в случае неограниченного стержня с начальным условием u(x,0) = ϕ(x)?

A)  с помощью формулы u(x,t)          =

.

n=1

B)  по  формуле        u(x,t)   =

.

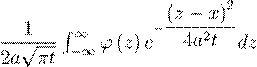C)  .

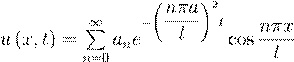37. Какойвидимеетуравнениетеплопроводности для нестационарного случая?

A)  ∆u = 0.

B)  u_t = a²∆u. C) u_tt = a²∆u.

38. Задача u_t = a²u_xx, 0 < x < l, t >

0; u(x,0) = ϕ(x), u_x (0,t) = u_x (l,t) есть: A) первая краевая задача. B) вторая краевая задача.

C) третья краевая задача.

39. Поставить задачу о нестационарном распространении тепла в конечном стержне, концы которого теплоизолированы, а начальноераспределениетемпературыудовлетворяет условию u(x,0) = ϕ(x).

A)  u_t = a²u_xx, 0 < x < l, t > 0; u(x,0) = ϕ(x), u(0,t) = u(l,t) = 0.

B)  u_t = a²u_xx, 0 < x < l, u(x,0) = ϕ(x), u_x (0,t) = u_x (l,t) = 0.

C)  u_t = a²u_xx, 0 < x < l, u(x,0) = ϕ(x), u(0,t) = u_x (l,t) = 0.

40. Уравнение Пуассона имеет вид:

A)  u_t = a²∆u.

B)  ∆u = 0.

C)  ∆u = −f (x,y,z).