




































транспортировании матрицы ее определитель не меняется.
2. Если в матрице поменять местами две строки (столбца), то ее определитель умножится на -1.
3. Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столбца) на их алгебраические дополнения.
4. Если все элементы какой-нибудь строки (столбца) матрицы умножить на число k, то ее определитель умножится на k.
5. Если все элементы какой-нибудь строки (столбца) матрицы представляют собой сумму двух слагаемых, то определитель матрицы равен сумме двух определителей. У первого на месте этой строки стоят первые слагаемые, а у второго -вторые, а все остальные строки у всех трех определителей одинаковы.
6. Определитель матрицы не изменится, если к одной ее строке (столбцу) прибавить линейную комбинацию остальных строк (столбцов).
7. Если элементы одной строки умножить на соответствующие алгебраические дополнения другой строки и сложить, то получится 0.
8. Линейная комбинация алгебраических дополнений элементов какой-нибудь строки равна определителю, у которого на месте этой строки стоят соответствующие коэффициенты линейной комбинации, а остальные строки совпадают со строками данного определителя.
Достаточные признаки равенства нулю определителя:
1. Если все элементы какой-нибудь строки (столбца) матрицы равно нулю, то определитель равен 0.
2. Если в матрице есть две одинаковые строки (столбца),то ее определитель равен 0.
3. Если матрица содержит две строки, соответствующие элементы которой пропорциональны,то ее определитель равен 0.
Необходимое и достаточное условие равенства нулю определителя:
Для того чтобы определитель матрицы был равен 0, необходимо и достаточно,чтобы ее строки (столбцы) были линейно зависимы.
Для квадратных невырожденных матриц вводится операция обращения. т.е. нахождения обратной матрицы А-1,такой что А×А-1=× А-1×А= Е.
Следовательно, обращение невырожденной матрицы аналогично определению обратного для любого отличного от нуля числа
Алгоритм нахождения обратной матрицы А-1:
Вычислить det A, если det A ¹0, то А-1 существует;
Транспонирование матрицы А (замена строк на столбцы);
Нахождение присоединенной матрицы `А (замена каждого элемента aij,на алгебраическое дополнение Ai j)
Деление каждого элемента присоединенной матрицы`А на det A.
ПРИМЕР. Найти обратную для матрицы А=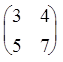 .Находим det A=3×7-5×4=1¹0.
.Находим det A=3×7-5×4=1¹0.
Находим
транспонированную матрицу АТ=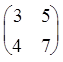 Находим
присоединенную матрицу`А=
Находим
присоединенную матрицу`А=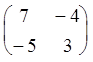 =А-1.
=А-1.
Проверка А×А-1 ==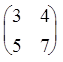 ×
×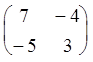 =
=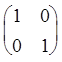 .
.
РАНГОМ МАТРИЦЫ называется наивысший порядок отличного от нуля определителя квадратной матрицы, получаемой из данной матрицы вычеркиванием некоторых строк и столбцов.
Для квадратной матрицы n´n, если определитель не равен 0, то ее ранг
R(A) = n. Если определитель равен 0, то можно с помощью метода Гаусса привести ее к ступенчатой. При этом образуются строки, состоящие из одних нулей. Тогда R(A) будет равен: R(A) = n- k, где k - количество нулевых строк.
ПРИМЕР. Определить R(A), если A =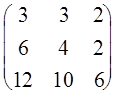 Решение.
Используем метод Гаусса. Умножим 1 строку на 2 и вычтем из 2-ой, умножим 1 строку на 4 и вычтем из 3-ей, получаем: A'=
Решение.
Используем метод Гаусса. Умножим 1 строку на 2 и вычтем из 2-ой, умножим 1 строку на 4 и вычтем из 3-ей, получаем: A'=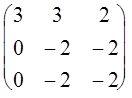 .
Вторую строку вычтем из третьей: A''=
.
Вторую строку вычтем из третьей: A''= 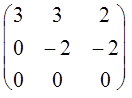 .Таким
образом, R(A) = 3 - 1 = 2.
.Таким
образом, R(A) = 3 - 1 = 2.
Пример. Найти ранг матрицы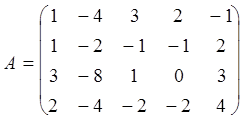 Вычтем 1 строку из 2-ой, затем 1 строку умноженную на 3 и вычтем из 3-й и умноженную 1 строку на 2 и вычтем из 4-ой
Вычтем 1 строку из 2-ой, затем 1 строку умноженную на 3 и вычтем из 3-й и умноженную 1 строку на 2 и вычтем из 4-ой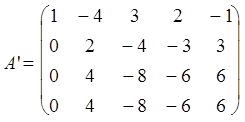 Вычтем 2
строку умноженную на из 3-й и 4-ой
Вычтем 2
строку умноженную на из 3-й и 4-ой 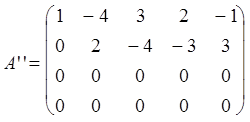 . Следовательно, R(A) =2
. Следовательно, R(A) =2
порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы: АЕ=ЕА=А.
Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица – частный случай скалярной матрицы.
Из приведенных ниже вычислений видно, что умножением на матрицы специального вида можно переставить в матрице столбцы или строки, вычислить сумму элементов любых строки или столбца, получить матрицу, равную каким–либо строке или столбцу матрицы, реализовать операцию умножения матрицы на число.
ЗАДАНИЕ 1.1
Умножая на матрицы специального вида, сформируйте матрицу–столбец и матрицу–строку, соответственно равные j–му столбцу и i–ой строке матрицы А. Вычислите суммы элементов j–ro столбца и i–ой строк матрицы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.