2.1. ЛИНЕЙНОЕ ПРОСТРАНСТВО. ОСНОВНЫЕ ПОНЯТИЯ
Пусть М – множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
•паре элементов хÎ М, уÎ М отвечает элемент х + уÎ М, называемый суммой элементов х и у;
• паре х, α, где хÎ М и α – любое действительное число, отвечает элемент αxÎ М, называемый произведением числа α и элемента х.
Будем называть множество М линейным пространством, если для его элементов определены операции сложения и умножения на действительное число и для любых элементов х, у, z Î М и произвольных α, β справедливо:
1. x+ у = у + x, сложение коммутативно;
2. х + (у + z) = (х + у)+z, сложение ассоциативно;
3. существует нулевой элемент 0 Î М такой, что х + 0 = x;
4. для каждого элемента существует противоположный элемент –х такой, что х + (–х) = 0;
5. α(βх) = (αβ)х, умножение на число ассоциативно;
6. 1×x = x;
7. α(х + у) = αх +αy, умножение на число дистрибутивно относительно сложения элементов;
8. (α + β)х = αх + βх, умножение вектора на число дистрибутивно относительно сложения чисел.
Равенства 1–8 называют аксиомами линейного пространства. Линейное пространство часто называют векторным пространством, а его элементы – векторами.
Говорят, что элемент (вектор) линейного пространства L линейно выражается через элементы (векторы) e1, e2, …, en Î L, если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде х = α1e1 + α2e2+ …+αnen.
Если хотя бы один вектор системы e1, e2, …, en векторов линейного пространства L линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой. Система векторов, которая не является линейно зависимой, называется линейно независимой.
Справедливо следующее утверждение.
Система e1, e2, …, en векторов линейного пространства L линейно независима тогда и только тогда, когда из равенства α1e1 + α2e2+ …+αnen = 0 следует равенство нулю всех коэффициентов: α2 = 0, α2 = 0, ...,αn = 0.
Если в линейном пространстве L существует линейно независимая система из n векторов, а любая система из (п+1)–го вектора линейно зависима, то число n называется размерностью пространства L и обозначается n = dim(L). В этом случае пространство L = Ln называют п–мерным линейным пространством или п–мерным векторным пространством.
Любая упорядоченная линейно независимая система n векторов e1, e2, …, en п–мерного линейного пространства L образует базис пространства, и любой вектор х Î L единственным образом выражается через векторы базиса: х = x1e1 + x2e2+ …+xnen.
Числа x1, x2, …, xn называют координатами вектора х в базисе e1, e2, …, en и обозначают x = (x1, x2, …, xn). При этом для любых двух произвольных векторов n–мерного линейного пространства x = (x1, x2, …, xn), у = (y1, y2, …, yn) и произвольного числа α справедливо: x + у = (x1+y1, x2 + y2, …, xn + yn) и αx = (αx1, αx2, …, αxn). Это означает, что все n–мерные линейные пространства "устроены" одинаково: как пространство Rn векторов–столбцов из п действительных чисел, т.е. что все они изоморфны пространству Rn.
Линейные пространства X и Y называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам х и x' из X соответствуют векторы у и у' из Y", то вектору х+ х' соответствует вектор у + у' и при любом α вектору ах Î X соответствует вектор αу Î Y.
Изоморфизм n–мерных линейных пространств пространству Rn означает, что соотношения между элементами n–мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из Rnи операции с ними и что всякое утверждение относительно векторов из Rn справедливо для соответствующих элементов любого n–мерного линейного пространства.
Например, доказано, что система векторов e1, e2, …, en из Rп
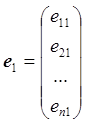 ,
, 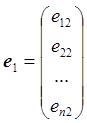 , …,
, …, 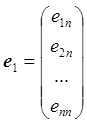
образует базис в Rn тогда и только тогда, когда отличен от нуля определитель матрицы со столбцами e1, e2, …, en:
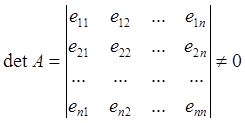 .
.
Для векторовe1, e2, …, en из Ln это означает, что они образуют базис в Ln тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов e1, e2, …, en.
Пусть e1, e2, …, en и f1, f2, …, fn, – два базиса в Ln.
Матрицей перехода от базиса e1, e2, …, en к базису f1, f2, …, fn дается матрица С, столбцами которой являются координаты торов f1, f2, …, fn в базисе e1, e2, …, en:
f2 = f12e1+ f22 e2+ …+ fn2 en, f2 = (f12 f22 … fn2 )T,
f1 = f11e1+ f21 e2+ …+ fn1 en, f1 = (f11 f21 … fn1 )T,
……………………………. …………………….
fn = f1ne1+ f2n e2+ …+ fnn en, fn = (f1n f2n … fnn )T,
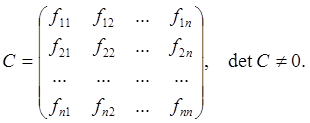
Вектор линейно выражается через векторы обоих базисов. Тогда, если х = х е1 + х2е2 + ... + хпеп = y1f1+ y2f2 + … + ynfn , то координаты, x1, x2, …, xn вектора в базисе e1, e2, …, en, и его координаты y1, y2, …, yn в базисе f1, f2, …, fn связаны соотношениями
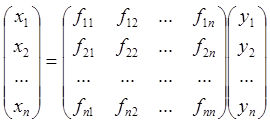 , или xе = Сxf, xf = С–1xе, если ввести обозначения xе = (x1, x2, …, xn)T и xf= (y1, y2, …, yn)T Для векторов–столбцов координат
вектора x в соответствующих базисах.
, или xе = Сxf, xf = С–1xе, если ввести обозначения xе = (x1, x2, …, xn)T и xf= (y1, y2, …, yn)T Для векторов–столбцов координат
вектора x в соответствующих базисах.
ЗАДАНИЕ 2.1
Докажите, что векторы f1 , f2 , f3, f4 образуют базис в пространстве L4, и найдите координаты вектора хТ={1 1 1 1}T в этом базисе
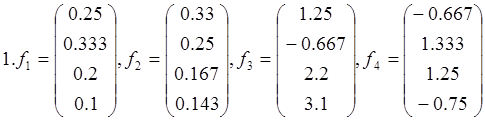
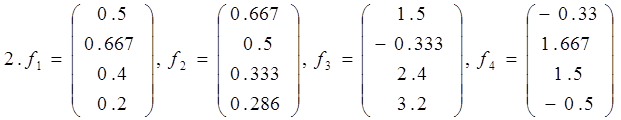
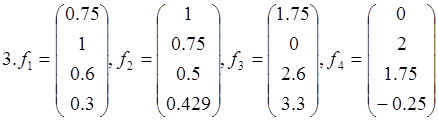
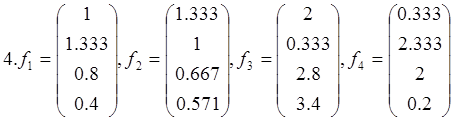
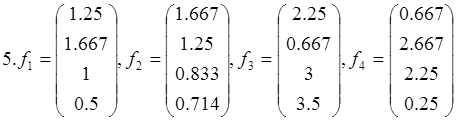
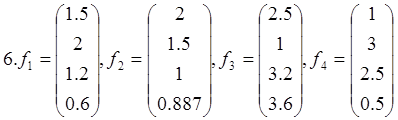
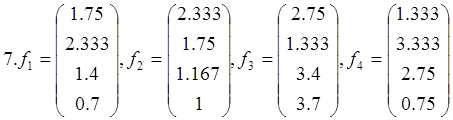
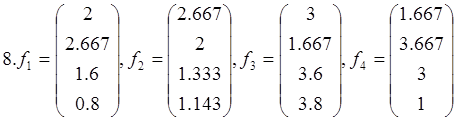
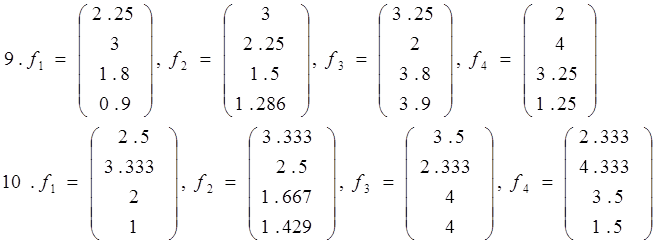
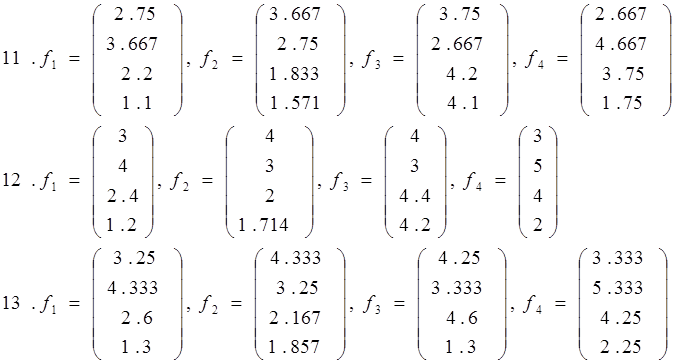
14. f1= , f2=
, f2=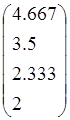 , f3=
, f3=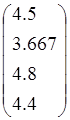 , f4=
, f4=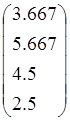 .
.
15. f1= , f2=
, f2=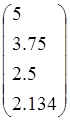 , f3=
, f3= , f4=
, f4= .
.
16. f1=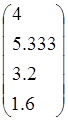 , f2=
, f2=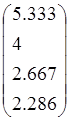 , f3=
, f3=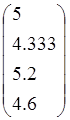 , f4=
, f4=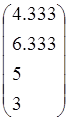 .
.
17.
f1= , f2=
, f2=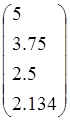 , f3=
, f3= , f4=
, f4= .
.
18.
f1= , f2=
, f2= , f3=
, f3= , f4=
, f4=![]() .
.
19.
f1= , f2=
, f2= , f3=
, f3=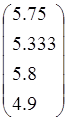 , f4=
, f4=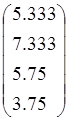 .
.
20.
f1= , f2=
, f2=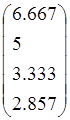 , f3=
, f3=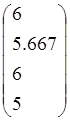 , f4=
, f4=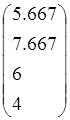 .
.
Порядок выполнения задания
1. Установите автоматический режим вычислений.
2. Введите матрицу C со столбцами f1, f2, f3, f4 .
3. Покажите, что определитель матрицы С отличен от нуля.
4. Вычислите матрицу, обратную к матрице С.
5. Запишите выражение и вычислите координаты вектора в базисе f1, f2, f3, f4.
6. Проверьте вычисления, выполнив обратный переход.
Пример выполнения задания
Докажите, что векторы 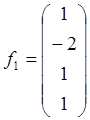 ,
, 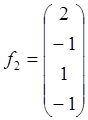 ,
, 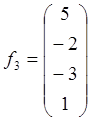 ,
, 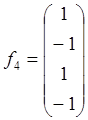 образуют базис в пространстве L4, и найдите
образуют базис в пространстве L4, и найдите
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.